想要知道什么是哈希表,得先了解哈希函数
哈希函数
地址index=H(key)
说白了,hash函数就是根据key计算出应该存储地址的位置,而哈希表是基于哈希函数建立的一种查找表
几种常见的哈希函数(散列函数)构造方法
直接定址法
- 取关键字或关键字的某个线性函数值为散列地址。
- 即 H(key) = key 或 H(key) = a*key + b,其中a和b为常数。
除留余数法
- 取关键字被某个不大于散列表长度 m 的数 p 求余,得到的作为散列地址。
- 即 H(key) = key % p, p < m。
数字分析法
- 当关键字的位数大于地址的位数,对关键字的各位分布进行分析,选出分布均匀的任意几位作为散列地址。
- 仅适用于所有关键字都已知的情况下,根据实际应用确定要选取的部分,尽量避免发生冲突。
平方取中法
- 先计算出关键字值的平方,然后取平方值中间几位作为散列地址。
- 随机分布的关键字,得到的散列地址也是随机分布的。
折叠法(叠加法)
- 将关键字分为位数相同的几部分,然后取这几部分的叠加和(舍去进位)作为散列地址。
- 用于关键字位数较多,并且关键字中每一位上数字分布大致均匀。
随机数法
- 选择一个随机函数,把关键字的随机函数值作为它的哈希值。
- 通常当关键字的长度不等时用这种方法。
构造哈希函数的方法很多,实际工作中要根据不同的情况选择合适的方法,总的原则是尽可能少的产生冲突。
通常考虑的因素有关键字的长度和分布情况、哈希值的范围等。
如:当关键字是整数类型时就可以用除留余数法;如果关键字是小数类型,选择随机数法会比较好。
什么是哈希表
哈希表(Hash table,也叫散列表),具有像数组那样根据随机访问的特性,是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
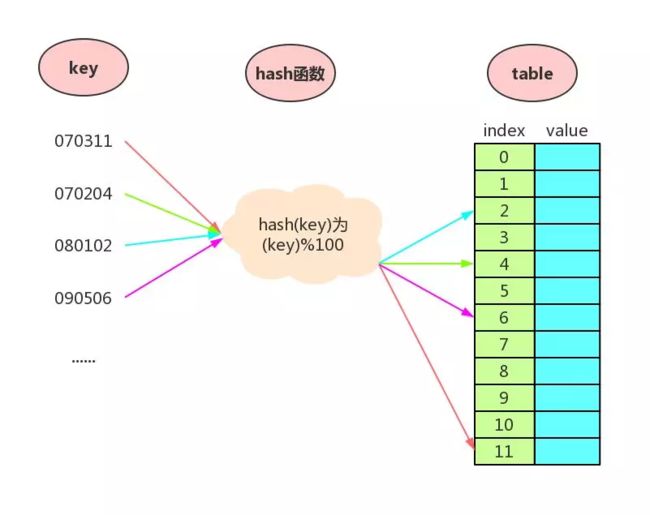
我们通过一个具体实例来理解散列表。当学校举办校运动会,每个运动员都有一个号码牌,这个号码牌的是根据“年级+班级+需序号”组成,比如初一三班的小岛的号码牌为 070311,其中 07表示七年级即初一, 03表示三班, 11表示班上第11个班上参加运动会的序号。
这个时候我们如何存储运动员的信息,来实现通过号码牌来查找运动员的信息?
按照以往的经验,我们可以通过使用数组来存储,其中号码牌即为数组的下标,数组的值为运动员的信息。但是这里有一个问题,运动员的号码牌不是连续的,而申请数组的时候内存空间是连续的,因此会有很多内存空间浪费。
这个时候就可以使用散列表,处理过程如下所示:
从上图可以观察到,我们在存储运动员信息的时候,不是将整个号码牌作为数组的下标,而是将号码牌先进行 hash函数(对100取余)处理后得到的数作为数组的下标,这样就可以数组的大小大大减小,并且在查找到时候也可以通过号码牌来查找对应的运动员的信息。
index=H(key)
这里的对应关系H称为散列函数,又称为哈希(Hash函数),采用散列技术将记录存储在一块连续的存储空间中,这块连续存储空间称为散列表或哈希表(Hash table)。
Hash Table的查询速度非常的快,几乎是O(1)的时间复杂度。
hash就是找到一种数据内容和数据存放地址之间的映射关系。
哈希冲突
细心的小伙伴观察到,如果 hash函数处理后的余数一样该怎么办?
即不同key值产生相同的地址,H(key1)=H(key2)
比如我们上面说的存储3 6 9
3 MOD 3 == 6 MOD 3 == 9 MOD 3
此时3 6 9都发生了hash冲突
解决冲突
设计合理的哈希函数可以减少冲突,但不能完全避免冲突。
所以需要有解决冲突的方法,常见有两类
开放定址法
如果两个数据元素的哈希值相同,则在哈希表中为后插入的数据元素另外选择一个表项。
当程序查找哈希表时,如果没有在第一个对应的哈希表项中找到符合查找要求的数据元素,程序就会继续往后查找,直到找到一个符合查找要求的数据元素,或者遇到一个空的表项。
例子
若要将一组关键字序列 {1, 9, 25, 11, 12, 35, 17, 29} 存放到哈希表中。
采用除留余数法构造哈希表;采用开放定址法处理冲突。
不妨设选取的p和m为13,由 f(key) = key % 13 可以得到下表。
需要注意的是,在上图中有两个关键字的探查次数为 2 ,其他都是1。
这个过程是这样的:
① 12 % 13 结果是12,而它的前面有个 25 ,25 % 13 也是12,存在冲突。
我们使用开放定址法 (12 + 1) % 13 = 0,没有冲突,完成。
② 35 % 13 结果是 9,而它的前面有个 9,9 % 13也是 9,存在冲突。
我们使用开放定址法 (9 + 1) % 13 = 10,没有冲突,完成。
拉链法(链表的数组)
将哈希值相同的数据元素存放在一个链表中,在查找哈希表的过程中,当查找到这个链表时,必须采用线性查找方法。
在这种方法中,哈希表中每个单元存放的不再是记录本身,而是相应同义词单链表的头指针。
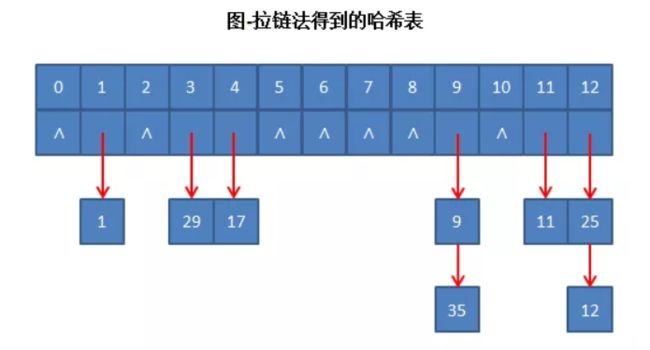
例子
如果对开放定址法例子中提到的序列使用拉链法,得到的结果如下图所示:
我们根据元素的一些特征把元素分配到不同的链表中去,也是根据这些特征,找到正确的链表,再从链表中找出这个元素。
元素特征转变为数组下标的方法就是散列法. 散列法当然不止一种,下面列出三种比较常用的:
除法散列法
最直观的一种,公式: index = value % 16
学过汇编的都知道,求模数其实是通过一个除法运算得到的,所以叫“除法散列法”。
平方散列法
求index是非常频繁的操作,而乘法的运算要比除法来得省时(对现在的CPU来说,估计我们感觉不出来),所以我们考虑把除法换成乘法和一个位移操作。公式:
index = (value * value) >> 28 (右移,除以2^28。记法:左移变大,是乘。右移变小,是除。)
如果数值分配比较均匀的话这种方法能得到不错的结果,但我上面画的那个图的各个元素的值算出来的index都是0——非常失败。也许你还有个问题,value如果很大,value * value不会溢出吗?答案是会的,但我们这个乘法不关心溢出,因为我们根本不是为了获取相乘结果,而是为了获取index。
斐波那契(Fibonacci)散列法
平方散列法的缺点是显而易见的,所以我们能不能找出一个理想的乘数,而不是拿value本身当作乘数呢?答案是肯定的。
1,对于16位整数而言,这个乘数是40503
2,对于32位整数而言,这个乘数是2654435769
3,对于64位整数而言,这个乘数是11400714819323198485
这几个“理想乘数”是如何得出来的呢?这跟一个法则有关,叫黄金分割法则,而描述黄金分割法则的最经典表达式无疑就是著名的斐波那契数列,即如此形式的序列:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377, 610, 987, 1597, 2584, 4181, 6765, 10946,…。另外,斐波那契数列的值和太阳系八大行星的轨道半径的比例出奇吻合。
对我们常见的32位整数而言,公式:
index = (value * 2654435769) >> 28
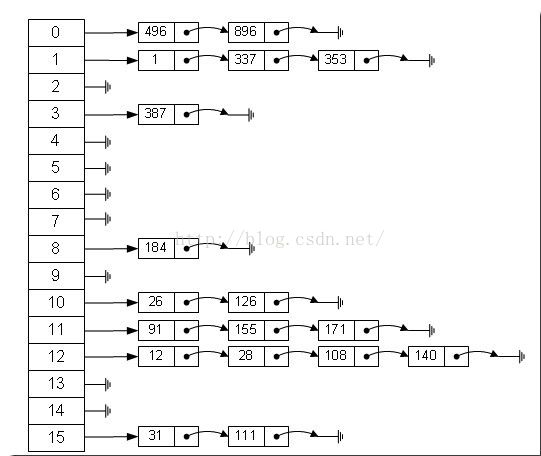
如果用这种斐波那契散列法的话,那就是从左图到右图这样了
注:用斐波那契散列法调整之后会比原来的取摸散列法好很多。
适用范围
快速查找,删除的基本数据结构,通常需要总数据量可以放入内存。
基本原理及要点
hash函数选择,针对字符串,整数,排列,具体相应的hash方法。
碰撞处理,一种是open hashing,也称为拉链法;另一种就是closed hashing,也称开放地址法,opened addressing。
Hash的应用
1、Hash主要用于信息安全领域中加密算法,它把一些不同长度的信息转化成杂乱的128位的编码,这些编码值叫做Hash值. 也可以说,Hash就是找到一种数据内容和数据存放地址之间的映射关系。
2、查找:哈希表,又称为散列,是一种更加快捷的查找技术。我们之前的查找,都是这样一种思路:集合中拿出来一个元素,看看是否与我们要找的相等,如果不等,缩小范围,继续查找。而哈希表是完全另外一种思路:当我知道key值以后,我就可以直接计算出这个元素在集合中的位置,根本不需要一次又一次的查找!
举一个例子,假如我的数组A中,第i个元素里面装的key就是i,那么数字3肯定是在第3个位置,数字10肯定是在第10个位置。哈希表就是利用利用这种基本的思想,建立一个从key到位置的函数,然后进行直接计算查找。
3、Hash表在海量数据处理中有着广泛应用。
问题实例(海量数据处理)
我们知道hash 表在海量数据处理中有着广泛的应用,下面,请看另一道百度面试题:
题目:海量日志数据,提取出某日访问百度次数最多的那个IP。
方案:IP的数目还是有限的,最多2^32个,所以可以考虑使用hash将ip直接存入内存,然后进行统计。