目录
- 2.1 图像处理技术概述
- 2.2 图像成像过程
- 2.2.1 视觉过程
- 2.2.2 成像变换
- 2.2.3 成像亮度
- 2.2.4 视觉系统对光的感知特点
- 2.2.5 采样和量化
- 2.3 像素间联系
- 2.3.1 像素的领域
- 2.3.2 像素间的邻接、连接和连通
- 2.3.3 像素间的距离
2.1 图像处理技术概述
- 图像采集:利用设备获取可输入计算机的数字图像,这些设备主要完成:
- 根据接收到的电磁能量产生模拟电信号
- 进一步将模拟电信号转化为离散形式
- 图像变换:将图像在不同空间转换的技术和过程
- 图像增强:对图像进行加工,得到对具体应用来说视觉效果更“好”,更“有用”的图像
- 图像恢复:根据图像退化的模型和知识重建或恢复原始的图像
- 图像编码:对图像进行加工,采用新的表达方法以减小表示图像所需数据量的技术和过程,又称图像压缩,在需要消除图像中冗余数据时使用
- 图像显示:多指 以空间亮度分布模式显示图像数据或其它类型的数据,主要目的:给人以直观可视的感觉
2.2 图像成像过程
需要考虑三个方面的问题:
- 几何:在图像中什么地方可发现目标?
- 辐射:图像中的目标有多亮,该亮度与目标和成像系统的光学特性有什么关系?
- 数字化和量化:当用一个数字矩阵表达图像并用数字计算机处理该图像会得到什么结果?
2.2.1 视觉过程
2.2.2 成像变换
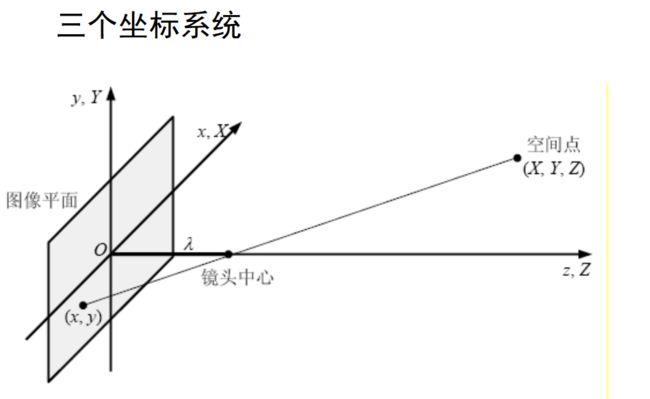
投影成像:将 3-D 客观场景 投影 到 2-D 图像平面
成像过程:三个坐标系统
- 世界坐标系统 \(X,Y,Z\)
- 摄像机坐标系统 \(x, y, z\)
- 图像平面 \(x,y\)
从 \(X, Y, Z\) 到 \(x,y,z\),从 \(x, y,z\) 到 \(x, y\)
2.2.3 成像亮度
2.2.4 视觉系统对光的感知特点
人眼适应的亮度范围:
- 总体范围大:从暗视觉门限到炫目极限之间的范围在 \(10^{10}\) 量级
- 具体范围小:一般范围在 \(10^{2}\) 量级
人类视觉系统 对亮度变化的感知 比 对亮度本身要敏感,人类视觉系统对光亮度的响应不是线性的,而是对数形式的。
2.2.5 采样和量化
\[ 图像 \rightarrow 数字图像 \\ f(x,y) \rightarrow l(r,c) \]
空间坐标的离散化叫做空间采样:\((x, y) \rightarrow (r,c)\)
幅度的离散化叫做幅度量化:\(f \rightarrow l\)
2.3 像素间联系
2.3.1 像素的领域
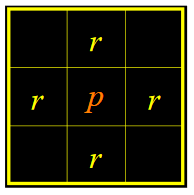
- 4-邻域——\(N_4(p)\)
- 对角领域——\(N_D(p)\)
- 8-领域——\(N_8(p)\)
2.3.2 像素间的邻接、连接和连通
邻接:仅考虑像素间的空间关系
- 连接:
- 是否邻接
- 灰度值是否满足某个特定的相似准则(同在一个灰度值集合中取值)
连通:连接是连通的一种特例,由一系列依次连接的像素组成
从具有坐标 \((x, y)\) 的像素 \(p\) 到具有坐标 \((s, t)\) 的像素 \(q\) 的一条通路由一系列具有坐标 \((x_0, y_0),(x_1, y_1),...,(x_n, y_n)\) 的独立像素组成。这里 \((x_0, y_0) = (x, y),(x_n, y_n) = (s, t)\),且 \((x_i, y_i)\) 与 \((x_i-1, y_i-1)\) 邻接,其中 \(1 ≤ i≤n\),\(n\) 为通路长度
4-连通,8-连通 ——>4-通路,8-通路
连接分为三种:
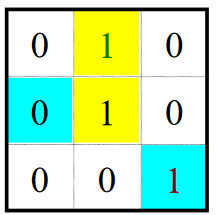
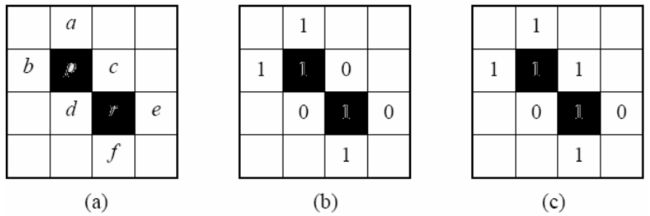
- 4-连接:2个像素 \(p\) 和 \(r\) 在 \(V\) 中取值且 \(r\) 在 \(N_4(p)\)中
m-连接(混合连接):2个像素 \(p\) 和 \(r\) 在 \(V\) 中取值且满足下列条件之一 :
混合连接的作用: 消除 8 连接可能产生的歧义性。
note:(a) 为原始图,(b) 为8-连接,(c) 为混合连接
一些定义:
- 对2个图像子集 \(S\) 和 \(T\) 来说,如果 \(S\) 中的一个或一些像素与 \(T\) 中的一个或一些像素邻接,则可以说图像子集\(S\) 和 \(T\) 是邻接的;
- 完全在一个图像子集中的像素组成的通路上的像素集合构成该图像子集中的一个 连通组元
- 如果S 中只有1个连通组元,即S 中所有像素都互相连通,则称S 是一个连通集
2.3.3 像素间的距离
距离度量函数的一些要求:
前提:3个像素 \(p,q,r\),坐标 $(x, y),(s, t),(u, v) $
- $0 \le D(p,q) $ (\(D(p,q)=0,当且仅当 p=q\))两个像素之间的距离总是正的
- \(D(p,q)=D(q,p)\) 距离和起点、终点无关
- \(D(p,r) \le D(p,q)+D(q,r)\) 最短距离是沿直线的
距离度量函数:
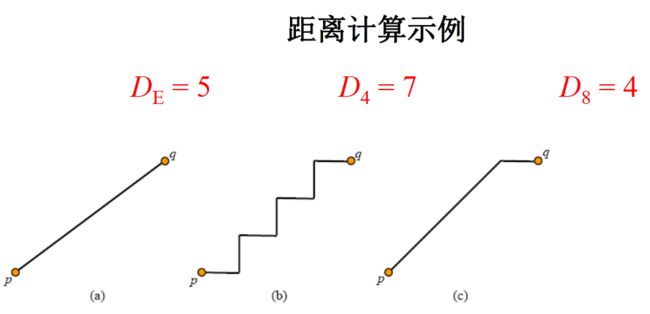
欧式距离
\[ D_E(p,q) = [(x-s)^2 + (y-t)^2]^{\frac{1}{2}} \]城区距离
\[ D_4(p,q) = |x-s|+|y-t| \]棋盘距离
\[ D_8(p,q) = \max(|x-s|, |y-t|) \]

其中,上图 \(D_1(p,q)\) 代表城区距离,\(D_2(p,q)\) 代表欧式距离,\(D_\infty(p,q)\) 代表棋盘距离
距离计算示例:
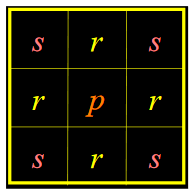
用距离定义领域:
4-领域:
\[ N_4(p) = \{r| D_4(p,r)=1\} \]8-领域:
\[ N_8(p) = \{r| D_8(p,r)=1\} \]