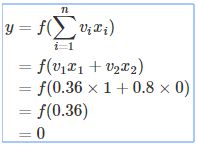http://krr.blog.shinobi.jp/javafx_praxis/java%E3%81%A7%E6%A9%9F%E6%A2%B0%E5%AD%A6%E7%BF%92%EF%BC%9A%E5%8D%98%E7%B4%94%E3%83%91%E3%83%BC%E3%82%BB%E3%83%97%E3%83%88%E3%83%AD%E3%83%B3%E3%82%92%E5%AE%9F%E8%A3%85%E3%81%97%E3%81%A6%E3%81%BF%E3%82%8B
近年来,人工智能和机械学习的话题热烈,特别是Deep learning这种机器学习的领域的关注度。2012年图像识别精度的比赛(ImageNet Large Scale Visual Recognition Challenge)Deep learnig利用队2位以下拉开很大的冠军。虽然不是特别新的概念,但由于这一功绩而被重新评价。与以后的利用扩大相关联(*1)。另外,在2015年,很多媒体报道,围棋用人工智能战胜了世界顶级棋士李世石。
(*2)。
作为程序员团体内部很在意的地方,所以查了一下,所谓DeepLearning,据说是“四层以上的新网络的学习”。总之,这次的基础知识和神经网络的概念进行了调查,实现了这一种的单层感知器,让人联想到机械学习的实现。顺便,本报道是从1开始实施,想利用库的看这篇『[Javaで機械学習 - Deeplearnig4j入門](http://krr.blog.shinobi.jp/site%20map#Javaで機械学習 - Deeplearning4j入門)』。
神经网络是?
神经网络和人类的脑功能参考的数学模型的事,神经元称为计算式连接到网络。计算式连接”,是有计算式的计算结果连接处的计算式的输入值的事。ーー利用,未知的计算式的(输入值,输出值)的组的近似式能创造。作为一个例子输入层、中间层•输出层的阶层构造持ーー以下所示。
层次结构的神经网络,神经元的集合层。各层的神经元前一层的神经元开始输入值领取,内部的线性函数(y = ax + b形函数)计算运行,计算结果也有一定的值(阈值)如果超越1,如果不把0输出值决定的。然后,第二层的神经元这输入输出值作为同样的计算,输出值的基础上又一个层的神经元进行计算…据说进行挪用了。因此,输入层赋值和出力层某种计算结果被输出,成为神经元内的线性函数的参数设定好的话希望能够制作的计算式的译。这是数值计算限定了的事,而是作为输入图像像素排列交货,输出和画像表示物体的分类值输出使这样的事情可能,神经网络机器学习广泛利用的。
但是,在那里的问题,“怎么神经元内的参数进行适当的设定?”。于是登场的学习。学习这么难听到,中学学习的几何学的世界考虑以下问题参数a,b追求同样的事情。
【问题】
函数“y = ax + b”通过点(0,3)和点(4,0)的时候,请回答a和b的值
【答案】
a=-¾
b=3
也就是说,输入x对于y知道的话,计算式中出现的参数(=适当的函数)可计算。上述的几何学的问题机械学习的观点来看,输入对应的数据组「( x,y )=( 0 3 ),( 4,0 )」是教师数据,被称为“线性函数y = ax + b”的参数a,b计算学习相当。当然,上述例子一样函数一次函数。如果知道瞬间准确的参数计算的,完全未知的函数对用别的方法参数近似这样的方法。这个参数的学习方法的不同和神经元连接方法,神经网络的各种各样的分类。
■感知器?
感知器是神经网络的一种,复数的投入2进制(0或1的排列)返回模型。感知器大致分为以下两类。
- 单层感知器
- 多层感知器
单层感知器是最简单的神经网络,输入和输出层只有模型。形象是以下。单层感知器2层只能线性分离可能的问题不能只解,线性分离可能的话一定能解开问题。这是一次函数(线性函数)在曲线(2次元以上的函数=非线性函数)表达不了,直线的话一定能表现的是一样的道理
计算式
单层感知器的神经元利用线性函数式表示如下。对于输入xi,以参数视图为重点,取得总和,总和超过了阈值的话,输出1,如果不是这样的话,就输出0
学习方法
单层感知器的学习方法被称为Delta定律。需要解答Delta定律有点难的公式(为了使误差函数最小而使用重降法,定义误差函数),但在编制程序的基础上只要利用结果就可以了,以下的公式按顺序更新参数。
在Delta定律中,如果输出与教师数据不同的情况下,在“t(教师数据)- o(推测的输出)”的方向上反复更新参数,总有一天会得到正确的参数(但是,因为利用重降法极为解决。也有容易陷入的缺点)。
在学习阶段,需要在正确的输出值之前进行标准三角则的参数更新,所以需要使用多数的教师数据的学习。但是,因为学习完成是为了不需要参数的更新,所以可以使用轻高速量的计算
另一方面,多层感知器3层以上的阶层的神经网络,被称为背景属性学习方法用单层感知器不能的线性非分离的问题也可以解了
■单层感知器的学习举动确认
用手计算来确认进行OR计算的单层感知器学习的行为。首先,关于单层感知器,作为输入的数n = 2,参数是如下的初始化。
这里的教师(输入数据)
给出的话,单层感知器的输出值如下计算
OR计算
输出,所以希望这个结果不正确的学习阶段进入。学习阶段Delta定律按照参数进行以下更新
更新后的参数的基础上寻求再次输出值以下。仍旧是不正确的,比以前更正确的回答有点接近,可以确认。这样做输入值如果反复改变学习,总有一天会正确输出吧
■安装程序
以下是单层感知器实施程序展示。实现了单层感知器学习OR的计算
import java.util.Random;
public class TestPerceptron
{
public static void main(String[] args)
{
// OR计算的教师数据
// 输入数据排列 x =(输入1,输入2)排列,正确数据排列 answer
final double[][] x = { { 1.0f , 1.0f } ,
{ 1.0f , 0.0f } ,
{ 0.0f , 1.0f } ,
{ 0.0f , 0.0f } };
final double[] answer = { 1.0f ,
1.0f ,
1.0f ,
0.0f };
// 感知器作成
// 初始状态的输出
Perceptron perceptron = new Perceptron( 2 );
System.out.println( "[init] " + perceptron );
// 学習
int succeed = 0; // 初始化连续正确次数
for( int i=0 ; i<1000 ; i++ )
{
// 空出行间
System.out.println();
System.out.println( String.format( "Trial:%d" , i ) );
// 选择使用的教师数据
int k = i % answer.length;
// 估计输出值
double outY = perceptron.output( x[k] );
System.out.println( String.format( "[input] %f , %f" , x[k][0] , x[k][1] ) );
System.out.println( String.format( "[output] %f" , outY ) );
// 评价・判定
if( answer[k] != outY )
{
// 初始化连续正确次数
succeed = 0;
// 学習
System.out.println( "[learn] before :" + perceptron );
perceptron.learn( answer[k] , outY , x[k] );
System.out.println( "[learn] after :" + perceptron );
}else{
// 更新连续正确的次数
// 所有的教师数据都有正确答案的话就结束了
if( ++succeed >= answer.length ){ break; }
}
}
// 所有的教师数据都有正确的正确答案
// 超过收敛限度数(1000次)的情况下结束
System.out.println( "[finish] " + perceptron );
}
}
/**
- 感知器代表
- ■x1 → V1
- ■ → y1
- θ
- ■x2 → V2
- x:入力
- y:出力
- v:結合加重
- θ:閾値
- 利用标准三角洲定律
*/
class Perceptron
{
// 内部変数
private int inputNeuronNum = 0; // 输入数
private double[] inputWeights = null; // 每个输入的加权
private double threshold = 0; // 閾値θ(临界值)
private double epsilon = 0.01f; // 学习用的定数ε
/**
* 初期化
* @param inputNeuronNum 输入的神经元个数
*/
public Perceptron( int inputNeuronNum )
{
// 变量初期化
Random r = new Random();
this.inputNeuronNum = inputNeuronNum;
this.inputWeights = new double[ inputNeuronNum ];
this.threshold = r.nextDouble(); // 随机生成阈值
// 用随机数初始化结合加权
for( int i=0 ; i threshold )? 1 : 0;
return out;
}
/**
* 全班内部确认的字符串输出
*/
@Override
public String toString()
{
// 输出文字列
String output = "weight : ";
for( int i=0 ; i }
■解说
作为感知器学习用的数据,准备了输入数据x /输出数据answer的组(16行~ 23行)。以这个教师数据为基础进行神经元显示函数计算,在输出值与教师数据不同的情况下,反复进行学习(32行~62行)。在学习发生时,进行“[ learn ]○○”的标准输出,从而能够看到内部参数的变化(第53行~55行)。 学习的结束条件是所有的教师数据都是正确的或者是一定次数(1000次)的循环执行。在上述执行中,从第127次的试行中「0 or 0 = 0」「1 or 1 = 1」「1 or 0 = 1」「1 or 1 = 1」和所有的教师数据是正确的。为此,试行结束了130次,学习结束了,也有试行4次结束的情况,也有1000次也不会结束的情况
感知器实施班中Perceptron,定义了初始化函数(101行~115行)、学习函数(123行~131行)・计算函数(138行~ 148行)。学习函数和计算函数是如上所述的实施。另外,在本程序中,为了实现每个执行的学习内容,作为参数的初始值,给予了随机数(110行~111行)