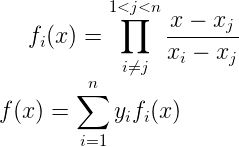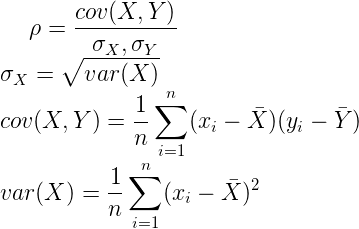特征工程总览

本章涉及到的知识点清单：

1、特征工程总览

2、数据预处理

2.1、无量纲化

2.1.1、标准化

2.1.2、区间缩放

2.2、特征二值化

2.3、特征哑编码

2.4、缺失值计算

2.4.1、均值补全

2.4.2、非线性插值补全

3、特征选择

3.1、Filter

3.1.1、方差选择法

3.1.2、相关系数法

3.1.3、卡方检验

3.2、Wrapper

3.2.1、递归特征消除法

3.3、Embedded

3.3.1、基于惩罚项

3.3.2、基于树模型

4、数据降维

4.1、PCA降维

4.2、LDA降维

5、案例演示

一、特征工程总览

由于原始数据集中可能会存在一些干扰无用的特征，为了过滤这些噪声，提高学习模型的准确度和效率，我们需要在建模前对整个数据集进行特征工程

特征工程的本质是一项工程活动，其目的是最大限度从原始数据集中提炼出有用的特征，以提供模型和算法使用

我们归纳总结出特征工程的总览图如下

特征工程总览

结合机器学习模型，我们可以概括出机器学习的整个工程步骤为

（1）数据获取：数据集的获取和存储

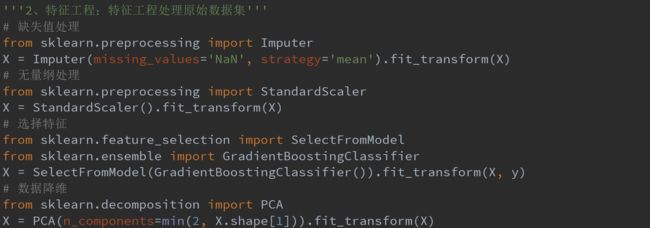
（2）特征工程：特征工程处理原始数据集

（3）建模：输入处理后的数据集进行模型训练

（4）调优：网格搜索对模型参数调优

（5）持久化模型

接下来我们细化特征工程的特征处理

特征处理分为以下三部分：

（1）数据预处理

（2）特征选择

（3）数据降维

二、数据预处理

通过特征提取，我们得到未经处理的特征信息，这些特征可能出现如下情况

（1）不属于同一个量纲

（2）定量特征的信息冗余：如学生的考试成绩，如果只关心“及格”和“不及格”，则可以将定量的考分，转化成"1"和“0”的离散值

（3）定性特征：如职业为医生、老师、银行职员等定性特征，可以进行自然数离散编码，也可以使用OneHot编码

（4）存在缺失值

我们把处理上述存在各种问题的原始数据的活动，称为数据预处理

原始数据为IRIS（鸢尾花）数据集

原始数据

2.1、无量纲化

我们可能需要将不同量纲下的特征数据转化为同一个规格，常见的无量纲化方法有标准化和区间缩放法

2.1.1、标准化

利用均值和标准差，将原始数据转换成标准正态分布的无量纲数据

标准化

标准化

标准化数据

2.1.2、区间缩放法

利用特征值的最小值和最大值进行缩放

区间缩放

区间缩放

区间缩数据

2.2、定量特征二值化

我们可能需要将定量特征数据转化为离散数据，使用二值化方法来设定一个阈值，大于阈值的赋值为1，小于等于阈值的赋值为0

特征二值化

特征二值化

二值化数据

2.3、特征哑编码

我们可能需要将离散值特征数据，转化为用整个离散空间的所有可能取值的位置表示，如总共[1，2，3]三种离散值情况，原始数据点值为2，则转化为[0，1，0]（对应第2个位置），这种方法称为特征哑编码，也称OneHot编码

OneHot编码

原始数据

OneHot编码数据

2.4、缺失值计算

有些特征数据里会存在缺省值，常见处理缺省值的方法有：丢弃缺失值样本、均值/中位数补全，非线性插值，或者通过一些监督机器学习模型，如KNN、ARIMA等

2.4.1、均值补全

通过计算缺省值所对应特征的所有特征值的均值/中位数来补全缺省值

均值补全

带缺省值的原始数据

均值/中位数补全缺省数据

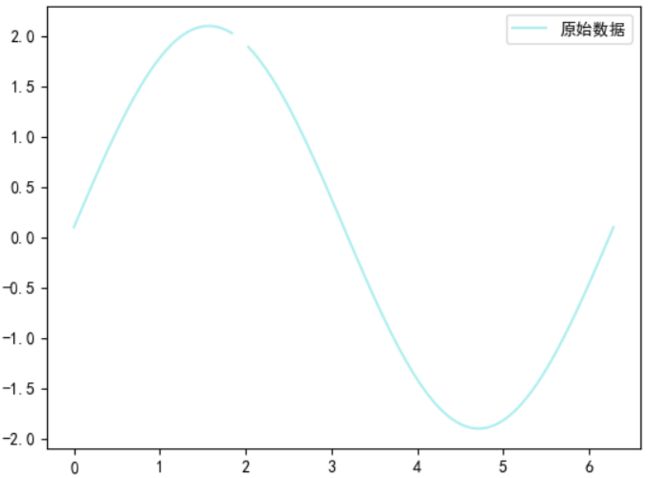
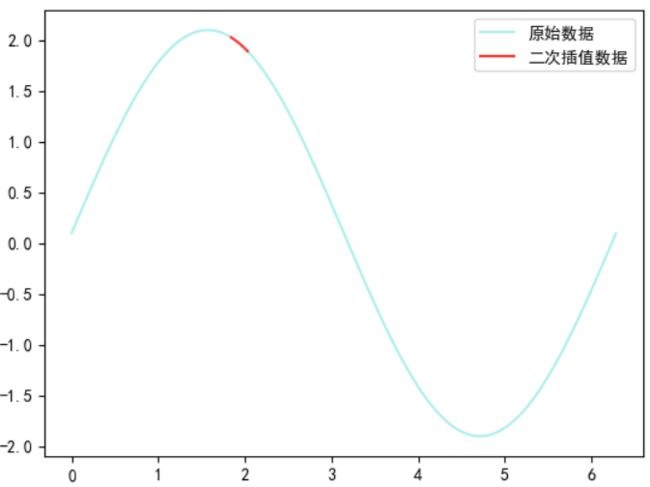
2.4.2、非线性插值补全

对于连续性变量，通过选取缺省值的邻域点，采用非线性插值补全缺省值，如牛顿插值、拉格朗插值等

拉格朗插值

带缺省值的原始数据

非线性插值补全缺省数据

三、特征选择

当完成数据预处理活动后，我们需要在数据集中选择有意义的特征，输入机器学习模型训练，以提高学习效率和性能

通常从两个方面考虑如何选取有意义的特征（过滤无用噪音）

（1）特征是否发散：如果一个特征不发散，例如方差接近于0，也就是说样本在这个特征列上基本上没有差异，说明该特征对于训练目标的区分没什么用

（2）特征与目标的相关性：与训练目标相关性较高的特征，应当优选选择

一般有三种特征选择的方法：

（1）Filter

（2）Wrapper

（3）Embedded

3.1、Filter

Filter即过滤法，从传统统计学出发，按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数，选择符合阈值条件的特征

包含下列统计量

传统的统计量

3.1.1、方差选择法

通过计算各个特征的方差，然后根据阈值，选择方差大于阈值的特征

方差选择法

方差选择法选择特征

3.1.2、相关系数法

通过计算各个特征对模型训练目标值的相关系数，然后根据阈值，选择相关系数大于阈值的特征

相关系数法

相关系数法选择特征

3.1.3、卡方检验

通过计算定性自变量对定性因变量的相关性，然后根据阈值，选择相关性大于阈值的特征

卡方检验

卡方检验选择特征

3.2、Wrapper

Wrapper即包装法，根据目标函数打分，每次选择若干特征，或者排除若干特征

3.2.1、RFE递归特征消除法

通过指定一个基模型，如LR或回归树来进行多轮训练，每轮训练后消除若干权值系数的特征，再基于新的特征集进行下一轮训练

递归特征消除法

递归特征消除法选择特征

3.3、Embedded

Embedded即集成法，先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，再根据系数从大到小选择特征

和Filter不同点的在于：Filter是通过传统统计量来选择过滤特征，而Embedded是通过机器学习模型给特征打分来选择特征

3.3.1、基于惩罚项

通过选取带L1或L2惩罚项的基模型来筛选特征

基模型带l1惩罚项

惩罚项的特征选择

3.3.2、基于树模型

通过选取如GBDT等树模型作为基模型来筛选特征

基于GBDT树模型

基于GBDT树模型的特征选择

四、数据降维

当完成特征选择的活动后，可以直接输入模型进行训练了

但是此时可能会出现：由于选择出的特征矩阵过于庞大，导致模型计算量偏大，训练时间较长

因此我们可能需要对特征矩阵进行降维处理

降维意味着信息的丢失，不过鉴于数据之间常常存在相关性，因此我们在降维的同时要将信息的损失尽量降低。常见的降维算法有PCA、SVD和LDA

4.1、PCA降维

PCA即主成分分析法，属于无监督学习，使得降维后数据的方差变大

PCA降维

PCA降维后的数据

4.2、LDA降维

LDA即线性判别分析法，属于监督学习，使得降维后数据有更好的分类性质（将高维分类数据投影到低维直线上，且使得不同分类点尽可能分开，相同类别点尽可能靠近）

LDA降维

LDA降维后的数据

五、案例演示

下面我们结合特征工程，加入到机器学习的工程步骤中

还是以IRIS（鸢尾花）为数据集

初始我们模拟加入一行缺省值和一列随机特征值

数据获取

特征工程

建模

调优

结果

案例代码见：特征工程总览