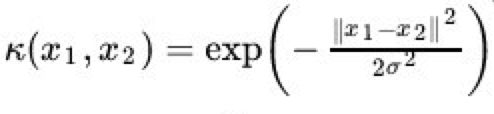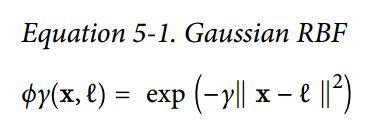通俗易懂理解核函数 in 《hands on machine learning with scikit-learn and tensorflow》
核函数的作用
某些数据在原始空间无法线性可分，可以将其映射到高维空间处理。
提问：如何映射？何种高维空间？
假设：映射为Φ，映射后的空间为Φ(x)
问题：要跟不知道我们要什么样的Φ
在高维空间中划分超平面主要涉及 样本xi 和 样本xj 之间的內积运算<Φ(xi),Φ(xj)>（这里具体参见西瓜书P126）
核函数的作用就是：k(xi,xj) = <Φ(xi),Φ(xj)>, 使得在低维空间操作xi,xj上完成高维Φ(xi),Φ(xj)想要完成的运算。
结合上图《hands on machine learning with scikit-learn and tensorflow》中的描述，做出个人理解：
核函数首先在samples上找1个landmark，然后计算其他所有数据同这个landmark的核函数距离，之后将这个距离作为一个特征使用。
如要生成更多的特征，那么就找更多的landmark，最多可以找到m个(m = the num of samples)
核函数是一种距离公式，它可以用来生成特征。
核函数的公式
这里只例举高斯核函数，我看过两种表达方式，分别为高斯核、高斯径向基函数如下：
高斯核，x1x2都是样本，σ是高斯带宽
高斯径向基函数RBF， l是landmark
核函数的代码
'''
np.linalg.norm(): 默认参数下求二范数，双竖运算符∥...∥ 表示Norm运算，即取向量的‘度量’
np.subtract(a,b)：a-b
---
高斯核函数：k(||x-xc||)=exp{- ||x-xc||^2 / (2*σ^2) }
xc为核函数中心
σ为函数的宽度参数
---
高斯核函数图像类似于一张纸中间隆起一块，σ越小则越尖
'''
def calc_gaussian(x, center, width):
return np.exp(-(np.square(np.linalg.norm(np.subtract(x, center))))/(2*np.square(width)))
for i in range(1,M):
phi[:,i] = calc_gaussian(x,landmark[i],1) # 设置了m个landmark
核函数逻辑回归
y = wx+b 无法完成分类，对x进行变化，x' = k(x,l) ==> y = wx'+b 可以对x'划分
已知x',y可以求出w,b
对new_x，进行变化new_x'，带入y = wx'+b，即可进行预测
为了提高预测准确性，往往会设置多个landmark求多个x'得到多个模型y = wx'+b
"""
===================================================================
Support Vector Regression (SVR) and Least Squares with Guassion Kernal
===================================================================
Source: https://github.com/JinScientist/Gaussion-Kernal-Least-Squares-Regression/
"""
print(__doc__)
import numpy as np
from sklearn.svm import SVR
import matplotlib.pyplot as plt
M=20 # number of kernal function
lamda=1 #regularization coefficient
############# Linear Combination of Gaussion(LGK) kernal
def LGK(M,x,y,lamda):
N=len(x)
mu=np.linspace(0, 6, M)
phi=np.zeros(shape=[N,M])
for i in range(1,M):
phi[:,i]=np.exp(-np.square(x-mu[i-1])/2).reshape(40,)
phiinv=np.linalg.pinv(phi)
w=phiinv.dot(y)
phiT=np.transpose(phi)
wr=np.linalg.inv(lamda*np.identity(M)+phiT.dot(phi)).dot(phiT).dot(y)
print('Dimension of Moore-Penrose pseudo-inverse:')
print(phiinv.shape)
print('Dimension of y:')
print(y.shape)
return(w,wr)#wr:regularized w
###########predict from trained LGK
def LGKpredict(M,w,x):
N=len(x)
phi=np.zeros(shape=[N,M])
mu=np.linspace(0, 6, M)
for i in range(1,M):
phi[:,i]=np.exp(-np.square(x-mu[i-1])/2).reshape(40,)
ypredict=phi.dot(w.reshape(M,1))
return(ypredict)
# Generate sample data
X = np.sort(5 * np.random.rand(40, 1), axis=0)
y = np.sin(X).ravel()
###############################################################################
# Add noise to targets
y[::5] += 3 * (0.5 - np.random.rand(8))
###############################################################################
# Fit regression model
(w,wr)=LGK(M,X,y,lamda)
y_LGK=LGKpredict(M,w,X)
y_LGK_r=LGKpredict(M,wr,X)
np.savetxt("w.csv", w, delimiter=",")
print('Dimension of W_ML:')
print(w.shape)
svr_rbf = SVR(kernel='rbf', C=1e3, gamma=0.1)
svr_lin = SVR(kernel='linear', C=1e3)
svr_poly = SVR(kernel='poly', C=1e3, degree=2)
y_rbf = svr_rbf.fit(X, y).predict(X)
y_lin = svr_lin.fit(X, y).predict(X)
y_poly = svr_poly.fit(X, y).predict(X)
###############################################################################
# look at the results
lw = 1
plt.scatter(X, y, color='darkorange', label='data')
plt.hold('on')
plt.plot(X, y_rbf, color='navy', lw=lw, label='RBF model')
plt.plot(X, y_lin, color='c', lw=lw, label='Linear model')
plt.plot(X, y_poly, color='cornflowerblue', lw=lw, label='Polynomial model')
plt.plot(X, y_LGK, color='maroon', lw=lw, label='Gausian kernal \n Least square model')
plt.plot(X, y_LGK_r, color='lime', lw=lw, label='Regularized Gausian kernal \n Least square model')
plt.xlabel('data')
plt.ylabel('target')
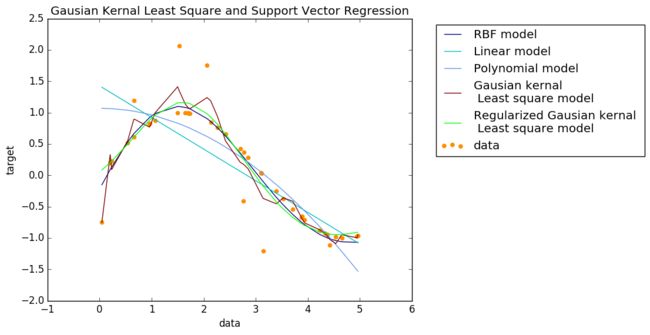
plt.title('Gausian Kernal Least Square and Support Vector Regression')
lgd=plt.legend(bbox_to_anchor=(1.05, 1), loc=2)
plt.savefig('SVR.png',bbox_extra_artists=(lgd,), bbox_inches='tight')
Github：Gaussion-Kernal-Least-Squares-Regression