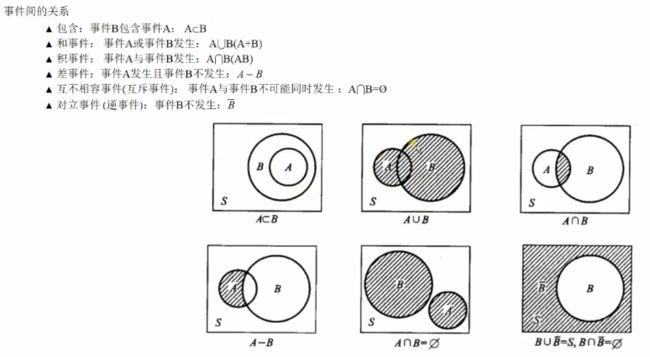
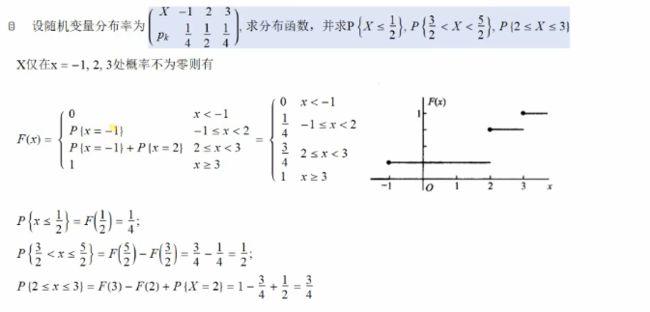
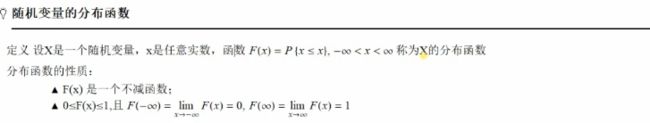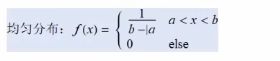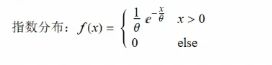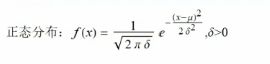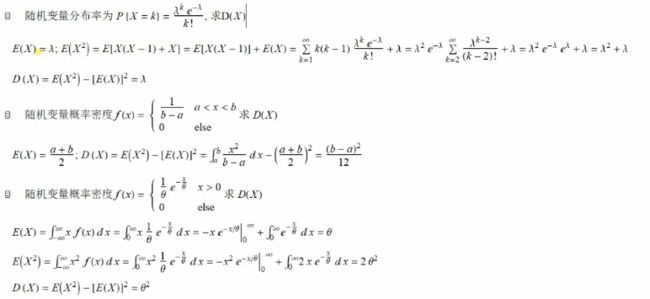概率论与数理统计以及Python 实现

概率论：

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  1 import numpy as np
  2 import pandas as pd
  3 import matplotlib.pyplot as plt
  4 
  5 #随机数  当随机种子设定时，随机数不变
  6 if 0:
  7     r = np.random.RandomState()
  8     # r = np.random.RandomState(10)
  9     res = r.rand(10)
 10     print(res)
 11     pass
 12 
 13 import numpy.random as r
 14 #均匀分布
 15 if 0:
 16     x = r.rand(1000)
 17     y = r.rand(1000)
 18     plt.scatter(x,y)
 19     plt.show()
 20     pass
 21 
 22 #正态分布  正态分布 - 标准正态分布，均值为0，方差为1
 23 if 0:
 24     x = r.randn(1000)
 25     y = r.randn(1000)
 26     plt.scatter(x,y)
 27 
 28     plt.show()
 29     pass
 30 
 31 # 正态分布
 32 # normal(loc=0.0, scale=1.0, size=None)
 33 # loc：均值，scale：标准差，size：抽取样本的size
 34 if 0:
 35     x = r.normal(10,5,1000)
 36     y = r.normal(10,5,1000)
 37     plt.scatter(x,y)
 38 
 39     plt.show()
 40     pass
 41 
 42 
 43 #指数分布
 44 if 0:
 45 
 46     lambd = 0.5
 47     x = np.arange(0,15,0.1)
 48     y = lambd* np.exp(-lambd*x)
 49     plt.plot(x,y)
 50 
 51 
 52     plt.show()
 53 
 54 
 55 
 56 #二项分布
 57 # .binomial(n, p, size=None)表示对一个二项分布进行采样,s为成功次数
 58 # P(N)=CsnPs(1−P)n−s
 59 # size:采样的次数  n:p即式中的n   p:函数的返回值表示n中发生/成功的次数s.
 60 
 61 # 同时抛弃9枚硬币，如果正面朝上少于5枚，则输掉8元，否则就赢8元。
 62 # 如果手中有1000元作为赌资，请问赌博10000次后可能会是什么情况呢？
 63 if 0:
 64     binomial = r.binomial(9, 0.5, 10000)  # 生成二项分布随机数
 65     # print(binomial)
 66     money = np.zeros(10001)  # 生成10001次赌资的列表
 67     money[0] = 1000 #一开始有1000
 68 
 69     for i in range(10000):
 70         if binomial[i] <5:
 71             money[i+1] = money[i] -8
 72         else:
 73             money[i+1] = money[i] +8
 74     plt.plot(np.arange(10001),money)
 75     plt.axvline(0,color='cyan',linestyle='--')
 76     plt.axvline(10001,color='gray',linestyle='--')
 77     plt.axhline(1000,color='cyan',linestyle='--')
 78     plt.show()
 79     pass
 80 
 81 
 82 # 二项分布
 83 # 将一枚硬币抛掷三次：恰好出现一次正面与至少有一次出现正面的概率
 84 if 0:
 85     # res = r.binomial(3,0.5,100)
 86     # plt.scatter(np.arange(100),res)
 87     # print(res)
 88     # plt.show()
 89 
 90     n0 = sum(r.binomial(3,0.5,10000) == 0)  #n0 是10000 次中有多少次 一个正面朝上也没有
 91     n1 = sum(r.binomial(3,0.5,10000) == 1)  #n1 是10000 次中有多少次 只有一个正面朝上
 92     n2 = sum(r.binomial(3,0.5,10000) == 2)  #n2 是10000 次中有多少次 只有两个正面朝上
 93     n3 = sum(r.binomial(3,0.5,10000) == 3)  #n3 是10000 次中有多少次 三个都正面朝上
 94     print(n0,n1,n2,n3)
 95 
 96     print("3个中一个正面也没有的概率是",n0/10000)  #1/8
 97     print("3个中只有一个正面的概率是",n1/10000)  #3/8
 98     print("3个中只有两个正面的概率是",n2/10000)  #3/8
 99     print("3个中都是正面的概率是",n3/10000) #1/8
100 
101 
102     pass
103 
104 
105 # 随机选择
106 if 0:
107     res = r.choice(['a','b','c','d','e','f'],size = 40)
108     print(res) #此时是随机选择40 个 ，放回的抽样
109 
110     res2 = r.choice(['a','b','c','d','e','f'])
111     print(res2)  #默认值是抽取一个
112     pass
113 
114 #随机顺序打乱
115 if 0:
116     a = np.arange(20)
117     res = r.shuffle(a)
118     # print(res)  #None
119     print(a)
120     pass
121 
122 
123 #随机变量的数字特征
124 
125 #方差计算
126 if 1:
127     a = r.randn(100) #创建个一个正态分布  标准的
128     # print(a)
129 
130     n = len(a) #元素个数
131     #均值
132     m = a.mean()
133     #方差
134     s = np.sum((a-m)**2)/n
135     print("均值为 {}  方差为 {} ".format(m,s))
136 
137     #numpy 提供的计算方差的函数 var()　
138     print("方差为 {} (Numpy 函数var 直接计算)".format(np.var(a)))
139 
140 
141 
142     pass

View Code

 

 

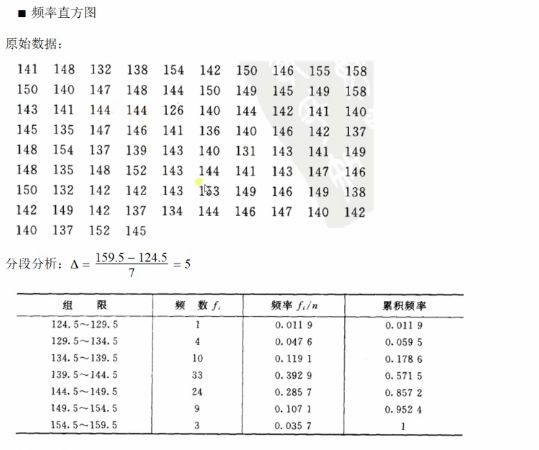
数理统计：

 

 

 

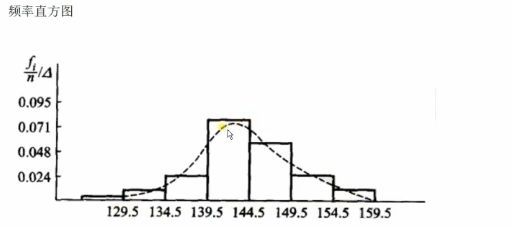
注：频率直方图　和　条形图是有很大区别的

 

 

 

 1 import numpy as np
 2 import pandas as pd
 3 import matplotlib.pyplot as plt
 4 
 5 #数据分布的图表可视化 - 直方图
 6 import numpy.random as r
 7 if 0:
 8     a =r.randn(1000)*100   #创建一个1000个数的  标准正态分布的数组
 9     # print(max(a),min(a))
10     # print(len(a))
11     plt.hist(a,bins=50)
12     # plt.grid() #显示网格线
13 
14 
15     plt.show()
16     pass
17 
18 # 数据分布的图表可视化 - 箱型图
19 if 0:
20     a = r.randn(1000)*100
21     plt.boxplot(a,
22                 vert=True,  # 是否垂直
23                 whis=1.5,  # IQR，默认1.5，也可以设置区间比如[5,95]，代表强制上下边缘为数据95%和5%位置
24                 patch_artist=True,  # 上下四分位框内是否填充，True为填充
25                 meanline=False, showmeans=True,  # 是否有均值线及其形状
26                 showbox=True,  # 是否显示箱线
27                 showcaps=True,  # 是否显示边缘线
28                 showfliers=True,  # 是否显示异常值
29                 notch=False,  # 中间箱体是否缺口
30                 )
31     plt.grid()
32     plt.show()
33 
34     pass
35 
36 #计算分位数
37 if 0:
38     # 用 numpy 求  分位数
39     if 1:
40         a = r.randn(1000)*100  #1000个
41         p25 = np.percentile(a, 25)
42         p40 = np.percentile(a, 40)
43         p75 = np.percentile(a, 75)
44         print('ar的25分位数为%.2f, 40分位数为%.2f, 75分位数为%.2f' % (p25, p40, p75))
45 
46         print("中位数 {} ".format(np.median(a)))
47         print("中位数 {} ".format(  np.percentile(a,50)  )   ) 
48 
49 
50     # 使用pandas中的dataframe 来求分位数
51     if 0:
52         a = r.randn(1000)*100
53         df = pd.DataFrame(a,columns=['value'])
54         # print(df)
55 
56         q25 = df['value'].quantile(0.25)
57         q40 = df['value'].quantile(0.4)
58         q75 = df['value'].quantile(0.75)
59         # print('df的25分位数为%.2f, 40分位数为%.2f, 75分位数为%.2f' % (q25, q40, q75))
60 
61         if 0:
62             q50 = df['value'].quantile(0.5)
63             print(q50)
64             print('df的中位数为%.2f' % df['value'].median())
65             pass
66 
67 
68         pass
69 
70 
71 
72 
73     pass

View Code