量子电路

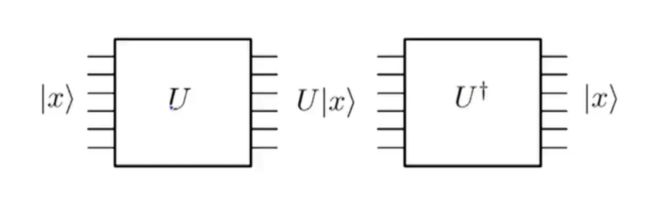
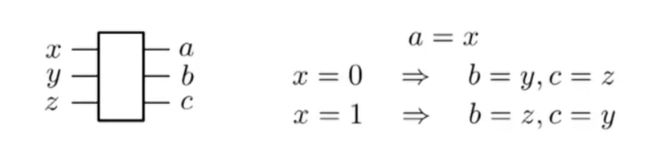量子电路的两点特殊

Axiom 1： Superposition principle

量子态是可以叠加的。

而叠加态的性质赋予了量子指数增长的可能。

一个量子比特就是二维Hilbert空间中的向量，两个量子比特就是四维Hilbert空间的中向量，三个就是八维， \(n\) 个量子比特就是 \(2^n\) 维Hilbert空间中的向量。

另外，需要注意的一点是，即使我只是在一个量子比特上操作，变化的也是整个系统。

Axiom 2： Unitary Evolution

量子电路和经典另一个重要的不同就是量子电路是可逆的。

经典电路没有可逆的要求，比如OR门，如果输出是１，你知道输入是什么吗？(1,1)、(1,0)、(0,1)都有可能，因为信息丢失了，四种输入的可能，输出却只有两种，信息丢失了。

而量子的操作变换则必须是酉变换，即，可逆，我可以根据我输出的信息反推我的输入。

量子可逆电路

经典可逆电路其实是比较容易的。

NOT门，他自己就是可逆的，取反再取反就是本身。

AND门，C-SWAP门其实就可以代替AND门

将z固定为0，则c只有在x和y都为1的时候为1，其余时候为0，满足AND门的要求。同时因为有a和b的存在，可以轻易的推导出x,y。

如果将希望能够从输出推导出输入，那么显然，会有junk bit(垃圾比特)的存在，即除了我们想要目标以外的结果，不是我们想要的目的，但是是我们推导输入不可或缺的存在，对于C-SWAP门来说，就是a,b。

junk bit对于经典比特来说，就是多出来的比特而已，但是对于量子比特来说，却是需要被remove的东西。如果不处理，会影响后续的计算。所以说，设计量子电路，第一个问题其实不是量子电路能够比经典电路加速多少倍，而是量子电路是否可以做到经典电路做到的事。

为什么要移除垃圾比特

对于经典比特来说，我不需要的比特，直接不要就可以了。我的后续操作中不涉及这些垃圾比特就没有关系，但是因为有量子相干的存在，如果我直接不管垃圾比特会让后续的测量得到完全不一样的结果。

例子：

令我们的目标函数是f(x)=x，A是没有垃圾比特的情况，即，我们输入什么输出什么。而B是有垃圾比特情况，第一个比特存目标答案，f(x)=x，第二个比特是我们的垃圾比特，假设这里的垃圾比特是junk(x)=x。

例子A：

在A的情况下，如果我们的输入是 \(\frac{1}{\sqrt2}|0\rangle + \frac{1}{\sqrt2}|1\rangle\) ，经过A门，还是 \(\frac{1}{\sqrt2}|0\rangle + \frac{1}{\sqrt2}|1\rangle\) ，在H门后，我们的比特又变成了 \(|0\rangle\) ，此时测量，得到的结果一定是 \(|0\rangle\) 。

例子B：

在B的情况下，如果我们的输入是 \((\frac{1}{\sqrt2}|0\rangle + \frac{1}{\sqrt2}|1\rangle)|0\rangle\) ，经过A门，则变成了\(\frac{1}{\sqrt2}|00\rangle + \frac{1}{\sqrt2}|11\rangle\) ，此时对第一个比特进行H门操作，得到结果 \(\frac{1}{2}|00\rangle + \frac{1}{2}|10\rangle+\frac{1}{2}|10\rangle - \frac{1}{2}|10\rangle\) 。此时对第一个比特测量，得到的结果是 \(|0\rangle\) 或者是 \(|1\rangle\) 的概率是一样的。

因为有了第二个比特的存在，所以上述式子中的 \(-\) 不能直接抵消第一个比特为 \(|1\rangle\) 的可能性，这也就是垃圾比特不得不移除的原因。

如何移除垃圾比特

垃圾比特对后续有影响，那么将他移除就好了，因为量子的操作是可逆的，所以怎么来的怎么回去。

但是在回去之前，把我们需要的目标 \(C(x)\) 的量子态用CNOT门复制出来就好。这样就得到了没有垃圾比特的结果。

可能有人想问，不是量子态不能复制吗？事实上，我们并没有复制 \(C(x)\) 的结果，当我们把结果从原来的比特上转移到y上后，原来的比特和垃圾比特又通过逆操作返回了最初的情况。垃圾比特最初的状态是 \(|0 \rangle\) ，并非叠加态的情况，量子的纠缠或者相干是因为有量子叠加态，不是纯态的原因，而今回到纯态，就不在造成影响。

参考资料：
Quantume Mechanics & Quantume Computation Lecture 7