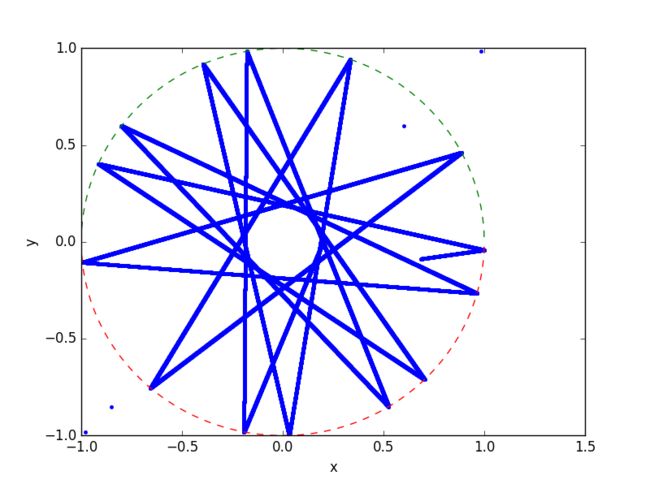
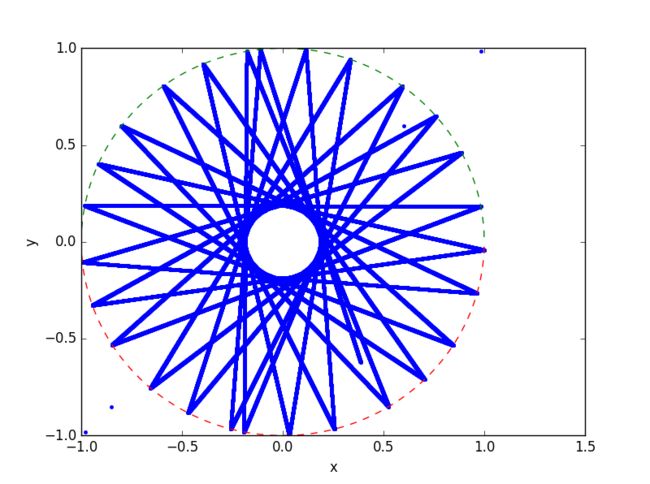
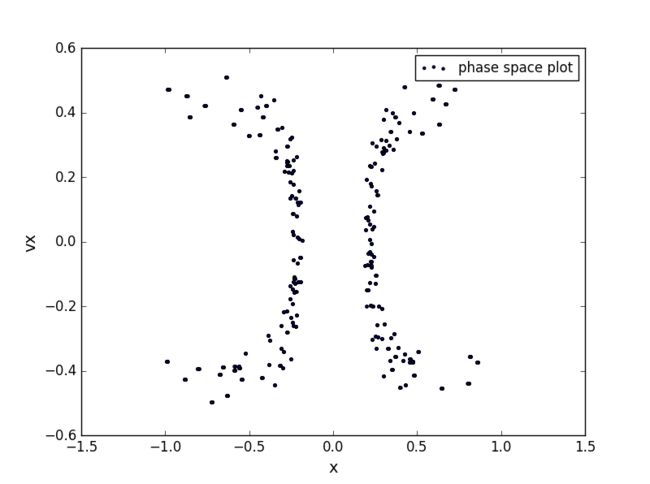
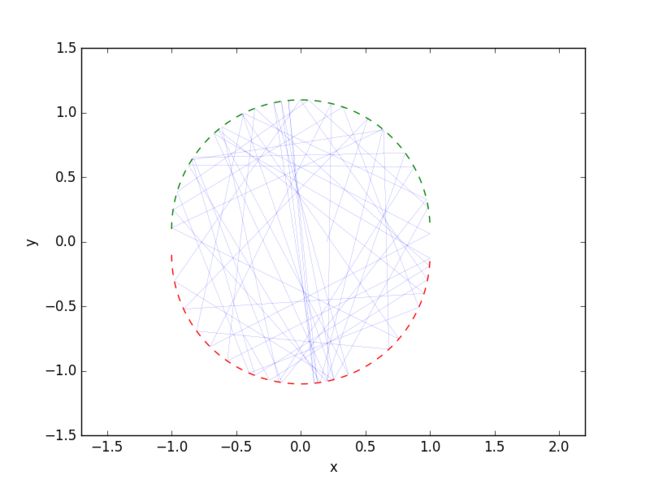
we consider a problem of a ball moving without friction on a perfect billiard table.Between collisions the velocity is constant so we have

After locatingthe collision point,We must next obtain the unit vector normal to the wall at the point of collision,

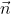![](http://latex.codecogs.com/png.latex?\vec n).

It is then useful to calculate the components of 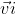![](http://latex.codecogs.com/png.latex?\vec vi)parallel and perpendicular to the wall.These are just

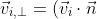![](http://latex.codecogs.com/png.latex?\vec v_{i,\bot}=(\vec v_i\cdot\vec n)\vec n)
![](http://latex.codecogs.com/png.latex?\vec v_{i,\parallel}=\vec vi-\vec v_{i,\bot})

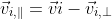
Hence,the velocity after reflection from the wall is

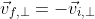
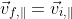
![](http://latex.codecogs.com/png.latex?\vec v_{f,\bot}=-\vec v_{i,\bot})
![](http://latex.codecogs.com/png.latex?\vec v_{f,\parallel}=\vec v_{i,\parallel})

code

#coding:utf-8
import pylab as pl
import numpy as np
import math


class tabel:
    def __init__(self, x0=0.2, y0=0, vx0=-0.2, vy0=-0.5, dtstep=0.001, total_time=50):
        self.x = [x0]
        self.y = [y0]
        self.vx = [vx0]
        self.vy = [vy0]
        self.time = total_time
        self.t = [0]
        self.dt = dtstep
        self.xbound=[-1]
        self.y1bound=[0]
        self.y2bound=[0]


    def run(self):
        for i in range(int(self.time / self.dt)):
            self.x.append(self.x[i]+self.vx[i]*self.dt)
            self.y.append(self.y[i] + self.vy[i] * self.dt)
            self.vx.append(self.vx[i])
            self.vy.append(self.vy[i])
            if (self.x[i+1]**2+self.y[i+1]**2>1):
                xtry=(self.x[i]+self.x[i+1])/2
                ytry=(self.y[i]+self.y[i+1])/2
                cos=xtry/(xtry**2+ytry**2)**0.5
                sin=ytry/(xtry**2+ytry**2)**0.5
                verticalx=-(self.vx[i]*cos+self.vy[i]*sin)*cos
                verticaly=-(self.vx[i]*cos+self.vy[i]*sin)*sin
                #parallelx=self.vx*sin**2-sin*cos*self.vy
               # parallely=self.vy*cos**2-self.vx*cos*sin
                parallelx=self.vx[i]+verticalx
                parallely=self.vy[i]+verticaly
                self.vx[i+1]=verticalx+parallelx
                self.vy[i+1]=verticaly+parallely
                #利用向量变换得到反弹后的速度vx和vy

                if (xtry**2+ytry**2>1):
                    self.x[i+1]=xtry
                    self.y[i+1]=ytry
                    continue
                else:
                    self.x[i]=xtry
                    self.x[i]=ytry
                    continue

    def bound(self):
        self.xbound= [-1]
        self.y1bound = [0]
        self.y2bound = [0]
        dx = 0.001
        for i in range (2000):
            self.xbound.append(self.xbound[i]+dx)
            self.y1bound.append((1-self.xbound[i+1]**2)**0.5)
            self.y2bound.append(-(1-self.xbound[i+1]**2)**0.5)
    def show(self):
        pl.plot(self.x,self.y,'.',label='tra')
        pl.plot(self.xbound,self.y1bound,'--',label='bound')
        pl.plot(self.xbound,self.y2bound,'--',label='bound')
        pl.xlabel(u'x')
        pl.ylabel(u'y')
a=tabel()
a.run()
a.bound()
a.show()
pl.show()

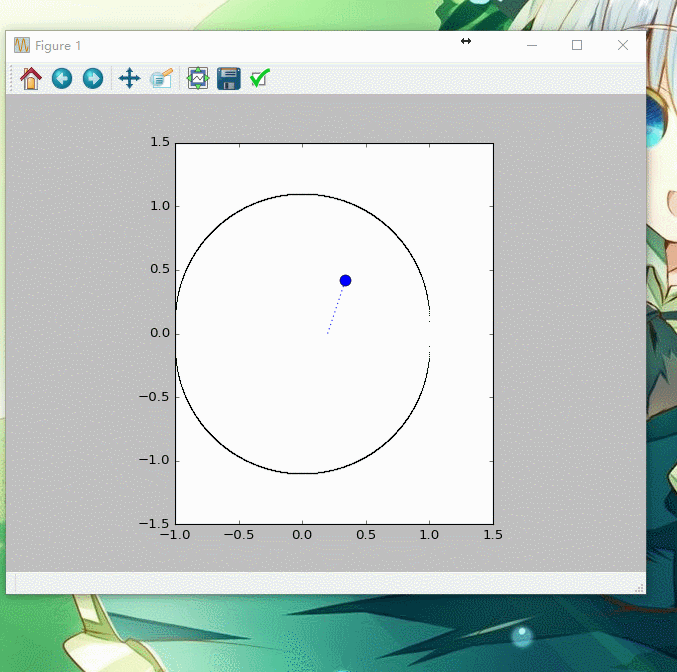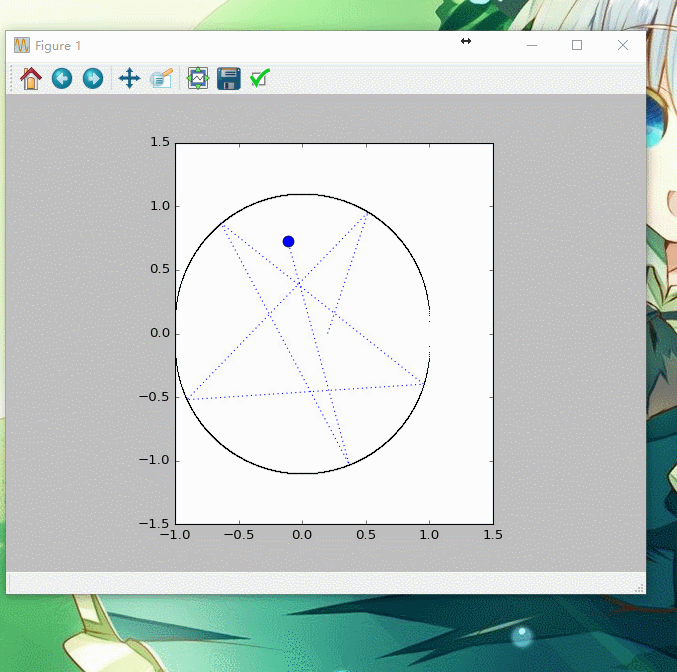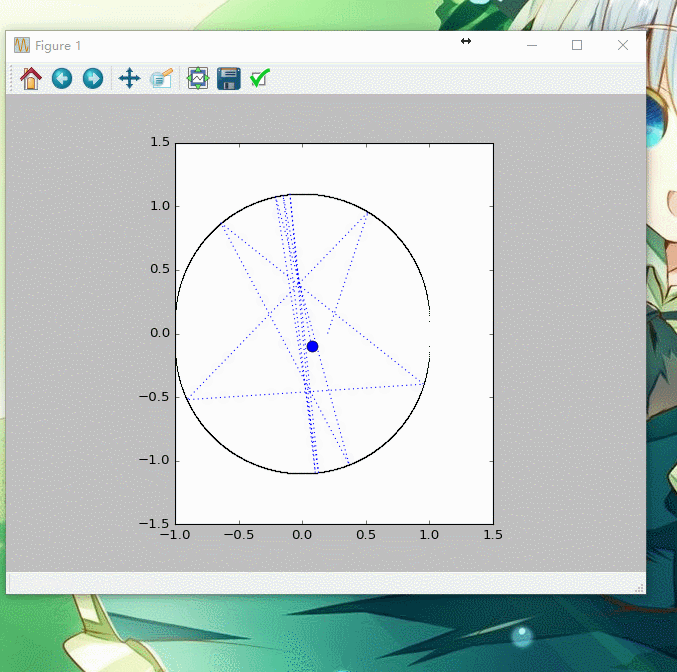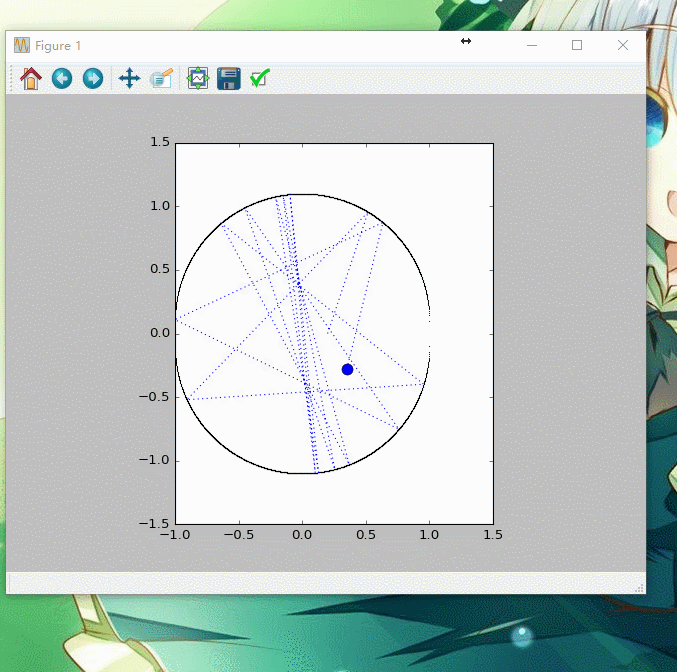
得到图像如下图所示

t=50，单位圆下反弹

t=100，单位圆下反弹

phase space plot

考虑到在两半圆间增加宽为2α的矩形，并得到动画，代码如下

#coding:utf-8
import pylab as pl
import numpy as np
import math
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import animation
#用于制作动画
class tabel:
    def __init__(self, x0=0.2, y0=0, vx0=0.1, vy0=0.3, dtstep=0.01, total_time=300,alpha=0.1):
        self.x = [x0]
        self.y = [y0]
        self.vx = [vx0]
        self.vy = [vy0]
        self.time = total_time
        self.t = [0]
        self.dt = dtstep
        self.xbound=[-1]
        self.y1bound=[0]
        self.y2bound=[0]
        self.alpha=alpha
    def run(self):
        for i in range(int(self.time / self.dt)):
            self.x.append(self.x[i]+self.vx[i]*self.dt)
            self.y.append(self.y[i] + self.vy[i] * self.dt)
            self.vx.append(self.vx[i])
            self.vy.append(self.vy[i])
            self.t.append(self.t[i]+self.dt)
            if( self.y[i]>=self.alpha):
                if (self.x[i+1]**2+(self.y[i+1]-self.alpha)**2>1):
                    xtry = self.x[i] + self.vx[i]*self.dt/200
                    ytry= self.y[i]+self.vy[i]*self.dt/200
                    dtrebound=self.dt/200
                    while(xtry**2+(ytry-self.alpha)**2<=1):
                        xtry = xtry + self.vx[i] * self.dt / 200
                        ytry = ytry + self.vy[i] * self.dt / 200
                        dtrebound=dtrebound+self.dt/100
                    self.t.append(self.t[-1]+dtrebound)
                    cos=xtry/(xtry**2+(ytry-self.alpha)**2)**0.5
                    sin=(ytry-self.alpha)/(xtry**2+(ytry-self.alpha)**2)**0.5
                    verticalx=-(self.vx[i]*cos+self.vy[i]*sin)*cos
                    verticaly=-(self.vx[i]*cos+self.vy[i]*sin)*sin
                    parallelx=self.vx[i]+verticalx
                    parallely=self.vy[i]+verticaly
                    self.vx[i + 1] = verticalx + parallelx
                    self.vy[i + 1] = verticaly + parallely#利用向量变换得到反弹后的速度vx和vy
                    self.x[i+1]=xtry
                    self.y[i+1]=ytry
            elif(self.y[i]-self.alpha):
                if (abs(self.x[i+1])>1):
                    xtry = self.x[i] + self.vx[i]*self.dt/100
                    ytry= self.y[i]+self.vy[i]*self.dt/100
                    dtrebound=self.dt/100
                    while(abs(xtry)<=1):
                        xtry = xtry + self.vx[i] * self.dt / 200
                        ytry = ytry + self.vy[i] * self.dt / 200
                        dtrebound=dtrebound+self.dt/100
                    self.vx[i+1]=-self.vx[i]
                    self.vy[i+1]=self.vy[i]
            elif(self.y[i]<-self.alpha ):
                if(self.x[i+1]**2+(self.y[i+1]+self.alpha)**2>1):
                    xtry = self.x[i] + self.vx[i] * self.dt / 200
                    ytry = self.y[i] + self.vy[i] * self.dt / 200
                    dtrebound = self.dt / 100
                    while (xtry ** 2 + (ytry + self.alpha) ** 2 <=1):
                        xtry = xtry + self.vx[i] * self.dt / 200
                        ytry = ytry + self.vy[i] * self.dt / 200
                        dtrebound = dtrebound + self.dt / 200
                    cos = xtry / (xtry ** 2 + (ytry+self.alpha) ** 2) ** 0.5
                    sin = (ytry+self.alpha)/ (xtry ** 2 + (ytry+self.alpha) ** 2) ** 0.5
                    verticalx = -(self.vx[i] * cos + self.vy[i] * sin) * cos
                    verticaly = -(self.vx[i] * cos + self.vy[i] * sin) * sin
                    parallelx = self.vx[i] + verticalx
                    parallely = self.vy[i] + verticaly
                    self.vx[i + 1] = verticalx + parallelx
                    self.vy[i + 1] = verticaly + parallely
                    self.x[i + 1] = xtry
                    self.y[i + 1] = ytry
    def bound(self):
        self.xbound= [-1]
        self.y1bound = [self.alpha]
        self.y2bound = [-self.alpha]
        dx = 0.001
        for i in range (2000):
            self.xbound.append(self.xbound[i]+dx)
            self.y1bound.append(self.alpha+(1-self.xbound[i+1]**2)**0.5)
            self.y2bound.append(-self.alpha-(1-self.xbound[i+1]**2)**0.5)
    def show(self):
        pl.plot(self.x,self.y,'-',label='tra',linewidth=0.1)
        pl.plot(self.xbound,self.y1bound,'--')
        pl.plot(self.xbound,self.y2bound,'--')
        pl.xlabel(u'x')
        pl.ylabel(u'y')
        pl.ylim(-1.1,1.1)
        pl.xlim(-1.1,1.1)
        pl.axis('equal')
        pl.show()

    def drawtrajectory(self):

        fig = plt.figure()
        ax = plt.axes(title=('Stadium with $\\alpha$ = 0.1, - divergence of two trajectories'),
                      aspect='equal', autoscale_on=False, xlim=(-1.1, 1.1), ylim=(-1.1, 1.1),
                      xlabel=('x'),
                      ylabel=('y'))


        line1 = ax.plot([], [], 'b:')  # 初始化数据，line是轨迹，point是轨迹的头部
        point1 = ax.plot([], [], 'bo', markersize=10)

        images = []

        def init():  # 该函数用于初始化动画

            line1 = ax.plot([], [], 'b:', markersize=8)
            point1 = ax.plot([], [], 'bo', markersize=10)
            bound1 = ax.plot([], [], 'k.', markersize=1)
            bound2 = ax.plot([], [], 'k.', markersize=1)
            return line1, point1, bound1, bound2

        def anmi(i):  # anmi函数用于每一帧的数据更新，i是帧数。
            ax.clear()
            bound1 = ax.plot(self.xbound, self.y1bound, 'k.', markersize=1)
            bound2 = ax.plot(self.xbound, self.y2bound, 'k.', markersize=1)
            line1 = ax.plot(self.x[0:20* i], self.y[0:20 * i], 'b:', markersize=8)
            point1 = ax.plot(self.x[20 * i - 1:20 * i], self.y[20 * i - 1:20 * i], 'bo', markersize=10)
            return line1, point1, bound1, bound2

        anmi = animation.FuncAnimation(fig, anmi, init_func=init, frames=500, interval=1, blit=False, repeat=False, )
        plt.show()


a=tabel()
a.run()
a.bound()
a.show
a.drawtrajectory()

得到下图

α=0.1

得到动画如图

动画.gif

Exercise_09:The billiard table