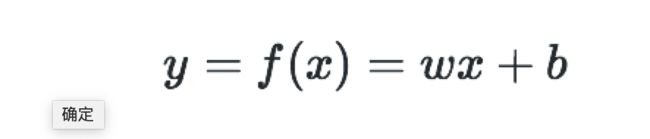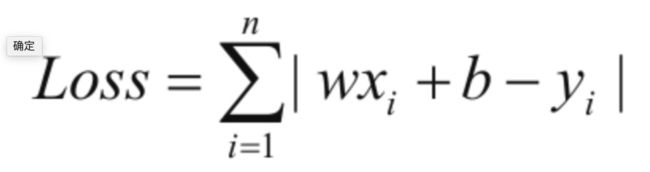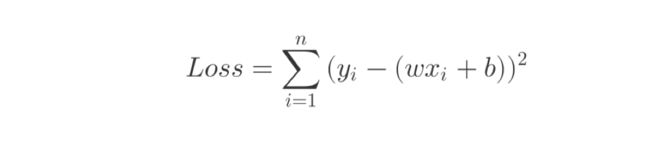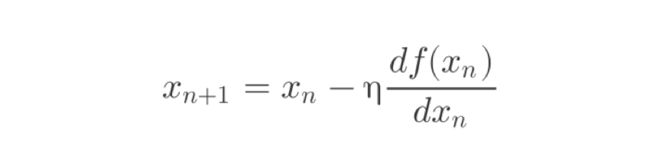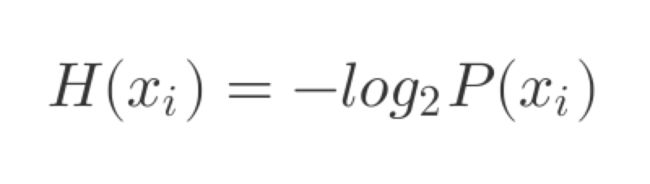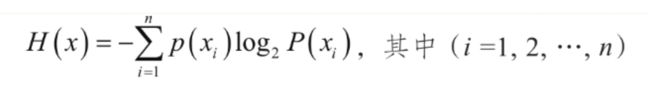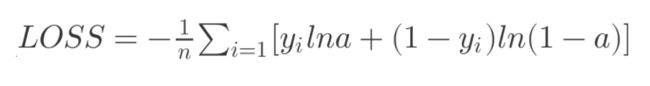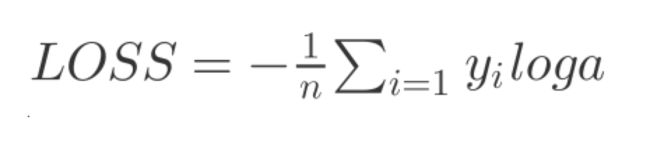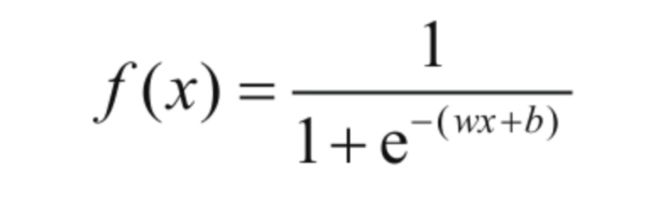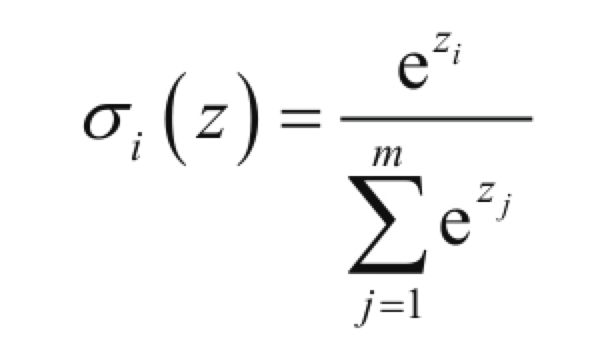1 机器学习分类
传统机器学习
机器学习可以理解成是生产算法的算法。需要人来先做特征提取,然后在把特征向量化后交给机器去训练。
传统机器学习分为 监督学习 和 无监督学习。深度学习
深度学习是基于深度神经网络的学习(DNN)。深度学习可以自动提取特征。深度学习可以采用 End-to-End 的学习方式,只需要进行很少的归一化和白化,就可以将数据交给模型去训练。
2 机器学习中的一些概念
首先我们需要了解几个机器学习中的起码要知道是怎么回事的概念,了解了后面看代码才不会一脸懵逼。
训练样本
就是用于训练的数据。包括了现实中的一些信息数据,以及对应的结果,也就是标签。训练
对训练样本的特征进行统计和归纳的过程。分类模型
总结出的特征,判断标准。验证
用测试数据集验证模型是否正确的过程。这个过程是在模型训练完后进行的,就是再用另外一些样本数据,代入到模型中去,看它的准确率如何。
2.1 聚类
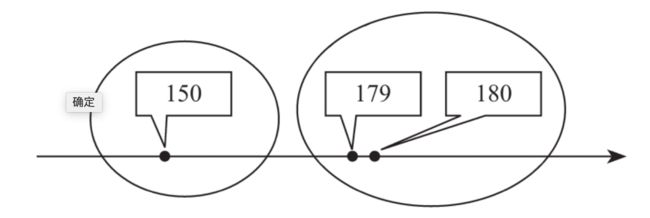
聚类 是一种典型的 无监督学习 ,是把数据进行分类的过程。
进行聚类的基本思想是,利用 向量 之间的距离 —— 空间中的 欧式距离 或 曼哈顿距离 , 根据距离的大小判断对象是否应该归为同一类别。
上图是对3个一维向量分类的例子。明显的能看到,离得近的两个们可以近似的认为它们属于同一类别。
2.2 回归
回归简单的说就是一个 由果索因 的过程。这是机器学习中很常用的一个手段。
回归分为:
- 线性回归
- 非线性回归
实际使用那种回归模型,需要根据情况而定。
2.2.1 线性回归
线性回归模型:
其中 w 是一个特征张量,储存着与每个变量x中元素对应的特征元素,x 就是输入的训练数据张量,b 是一个偏置量。
这其实就是高中概率与统计章节中常见的一个公式。就像解那时候的应用题一样,我们需要根据一堆 (x,y)求解一个合适的 w 和 b。
看看上面这个应用题,是否想起了高中时代的数学课?哈哈...
2.2.2 损失Loss函数
损失函数是用来评估模型预测结果和真实情况差距的,差距越小,说明我们的模型越好,越准确。
这,就是损失函数的公式!
当我们假设一个 w 和 b 后,循环计算每一个 x 所得的值和真实 x 所对应的值相减,然后将每一个差相加求和,得到一个差值之和,就是当前的损失。
损失越小,说明所寻找到的 w 和 b 就越合适,当 Loss 为 0 时,说明此时模型的准确率为 100% 。
事实上,这和高中概率与统计应用题,给你一堆 x,y ,然后求一个 系数w 和 常量b 出来是一样的一样的。只不过在计算机中,由于算力比手算强大太多了,所以我们可以一遍一遍的调整 w 和 b 这两个参数,使 Loss 一直向趋于 0 的方向移动 ,从而使模型的准确率趋于 100% 。
通常,为了使 Loss 始终保持为正 ,也会有如下损失函数:
求平方使得结果横为正数。
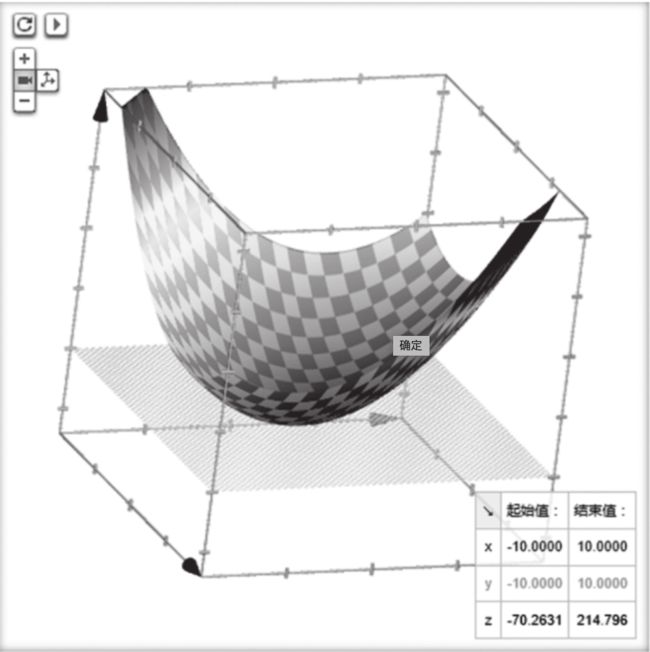
比如这个函数的图像可能是一个三维的碗,那么我们的任务就是找到碗底的位置,也就是极值,因为在该点有解,即损失最小。
2.2.3 梯度下降法寻找最优解
对于复杂函数,我们要直接求解是巨困难的,甚至有时可以说是处于不可解的状态。我们需要寻找损失函数的极值,可以使用牛顿迭代法的思想进行迭代寻找。
那对于复杂函数是不是就只能束手无策了呢?在你了解 牛顿迭代法 之后就可以回到不是了,而此前对于这个问题也许只能回答不能了。
通过迭代,我们可以逐步的逼近索要寻找的极值。
这里,我们还人为的引入了一个 η 参数,这个参数用于调整步长。步子迈大了可能会越过极值,迈小了有会产生很大的计算量,具体取多大合适,还是要多看看老司机们烫过的坑。
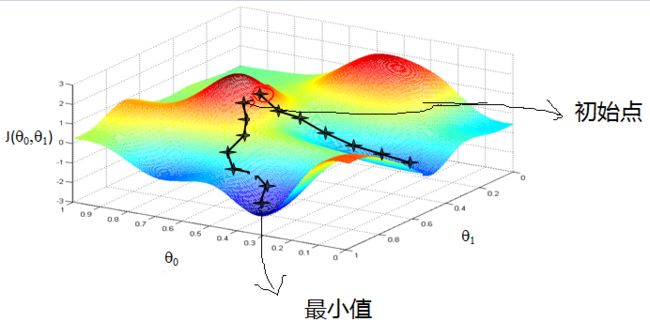
普通的梯度下降法(批梯度下降法,BGD),需要遍历所有的数据样本,在样本量不大的时候还是可以的,毕竟这么干精度起码是很高的。但是如果样本容量巨大,那每次遍历所有样本,必然都会消耗很多时间成本。并且如果我们的损失函数不是一个凸函数误差曲面就会存在多个局部极小值(即局部碗底),那采用这种方法可能会陷入局部最优解中。
如上图就是一个非凸损失函数,有可能在梯度下降的过程中走到了一个局部最低点去,而这其实不是真正的最低点。
为了加快收敛速度,随机梯度下降法(SGD) 就诞生了。它的思想是每次仅随机的抽取样本总体中的一个样本,来决定下一步的走向。它的好处是不用遍历所有的样本,所以对于样本容量巨大的情况,能够极大的加快收敛。但可想而知,每次随便取一个样本来更新权值,最终的权值很可能并不是最优解,不过有时在考虑现实情况的时候,这点精度误差也是可接受的。
那我们可不可以既要速度,又要精度呢?当 CoorChice 这么问的时候,你可就是知道套路问题的套路答案了(也许下次 CoorChice 就不会按套路走了,啊哈哈!)。答案就是 小批梯度下降法(Mini-batch GD)。它的思想是每次选取一定量的样本进行训练,然后再更新权值。即不用全部遍历,也不会因为每次更新仅由一个样本来决定而损失过多的精度。两头兼顾,当然也比较中庸。
2.2.4 交叉熵
在了解交叉熵之前,先了解一下什么是信息熵?
首先看两个相关公式。
信息量公式:
没错,通过对一种情况发生的先验概率进行对数计算的结果,被用来表征这种事件发生的信息量。
信息熵公式:
就是将所有事件的信息熵进行加和。这个值越大,表明对于预测一个事件而言的不确定性就越大。
上面的公式是 信息熵 公式,它表示对于一系列事件,根据其历史发生数据可以计算出一个先验概率,根据这个先验概率,可以计算出该事件发生的信息量,再将信息量乘以先验概率,就可以得到单个事件的熵。将这些事件的熵求和,就可以得到信息熵了。它有什么作用呢?就是用来量化信息量的,如果越不确定,则其信息熵就越大。对于一个有序的系统(按部就班)来说,它的信息熵就比较小了。
如果理解了信息熵,接下来就可以更进一步的了解交叉熵了。
首先,交叉熵损失函数如下:
y 表示期望输出值,a 表示实际模型的输出。
交叉熵是用来干什么的呢?它表示的训练结果和实际标签结果的差距。
交叉熵函数也有这种常用的形式:
通常交叉熵会和 Softmax 激励函数一起在输出层计算输出。
3 深度学习的基本概念
深度学习是基于深度神经网络的学习。它的概念类似与人的神经结构,由神经元可链接成一个神经网络,每个神经元被作为一个网络节点。
好像一下又回到了生物课!
深度学习相对于传统的机器学习来说,很明显的优势在于能够自动提取特征,可将线性不可分的问题转变为线性可分的问题。
使用传统机器学习,不管用朴素贝叶斯、决策树、支持向量机SVM等分类模型之前,必须对大量的模型进行处理,人工的从中提取特征用于量化。而在深度学习中,通过大量的线性分类器的堆叠,加上一些非线性因素,可以使一些特征能够自动的显现出来,而干扰因素经过过滤也能很大程度的被忽略。
总之,这种方式的机器学习肯定是更加先进的,但是需要消耗的资源也会更大。
深度学习由于是自动提取特征的,所以会导致我们有时候无法判断处究竟为什么会是这个模型,不便于我们分析问题,它就像一个黑盒一样,给它数据,它给你结果,而你很难了解里面发生了什么。
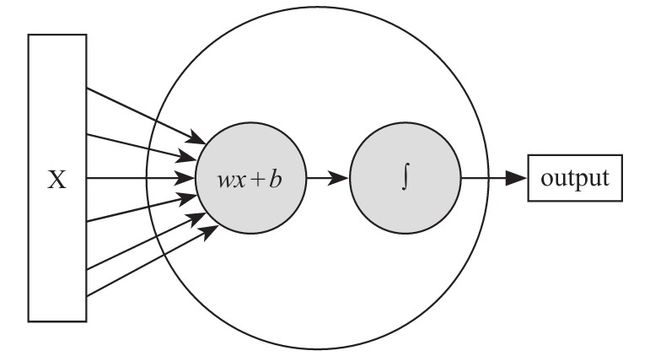
3.1 神经元的组成
通常,一个神经元由一个 “线性模型” 和 一个 “激励函数” 组成。线性模型其实就是上面提到过的线性回归模型。
如图就是一个神经网络,它共有两层,一个是神经元层(隐含层),一个是输出层。通常我们在说一个网络的深度时,是不会把输入层不计入的。
在神经元中,有一个线性模型 wx + b 和 一个激活函数 f。
我们的数据将会通过一个个的神经元,每个神经元都有一组权重,用于提取一类特征,相当于是我们把数据进行了一层一层的剖析。
3.2 激励函数
激励函数,通常也会被称为激活函数,它是跟随在 f(x) = wx + b 函数之后,用来加入一些非线性的因素的。通过激活函数,可以将线性函数作为输入,经过激活函数后,变成非线性的,这样一来就更接近真实世界的复杂情况了。
列举几个常用的激活函数,有助理解。
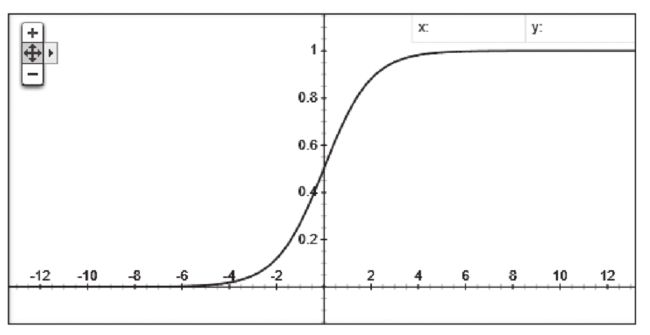
3.2.1 Sigmoid函数
图像
从函数可以看到,这个函数的值域为 (0,1),0.5值处为函数的对称中心。有时在 <-4 和 >4 的区间中,函数曲线越来越趋于水平,也就是导数很趋于0,这会导致梯度下降时,我们的对权值的更新微乎其微,也就是出现梯度消失的问题。
当然,它作为比较常用的激励函数,有其自己很适用的问题领域,比如二分类问题。
3.2.2 ReLu函数
y = max(x, 0)
图像
这是个很受欢迎的函数,光是看看它简洁的函数式你就不能拒绝它!
这个函数在 > 0 的时候,输入就等于输出,计算量会小很多,所以收敛速度会快很多。
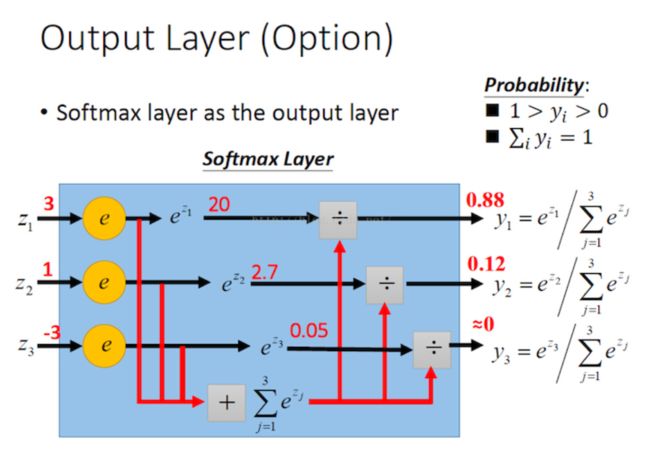
3.2.3 Softmax
这个函数看起来比较复杂,它通常被用于处理多分类问题。可以看看它的定义式,就是个体在总体中的占比情况。
从图中可以很直观的看出这个函数的功能,就是各种分类的概率啊。
3.3 独热编码
对于多分类问题,标注分类可以使用使用 独热编码 来进行,比如这样一个例子:
就是说,有几个类型就定义一个几维的向量,然后向量中只有一个元素为1,其余均为0,通过1在向量中的位置来表示类型。
3.3 过拟合和欠拟合
在训练过程中,可能会因为过拟合或者欠拟合而导致最终训练出来的模型准确率不足或者因泛化性差而导致准确率低。
欠拟合
样本过少,无法归纳出足够的共性过拟合
参数过多,导致在训练集上准确率很高,但换新样本会严重误判。
总结
在了解了机器学习是干什么的之后,又了解了一些基本概念在机器学习中会被经常用到的,相信你对机器学习也不会保持一种敬畏感了,知道它很厉害,但是不知道为什么厉害。
现在开始,可以试着到 TensorFlow 官网看一些入门的 code 例子,然后结合这些概念理解下每个步骤是在干什么,为什么要这么做?
在前面,大家也会看到,在机器学习中用到了很多统计学的知识,所以很多人会认为机器学习其实就是统计学而已。实际上 CoorChice 认为,机器学习只是用了统计学作为工具,去研究解决问题,实际上它是有一套自己的理论和套路的,就像物理用数据作为工具去解决问题一样。机器学习在解决实际问题的过程中,会需要很多学科的交叉来分析问题,构建模型。当然,总体的思想看起来还是很简单的,只不过面对真世界中的复杂情况下,其探寻求解过程会比较复杂。
- 抽出空余时间写文章分享需要动力,还请各位看官动动小手点个赞,给CoorChice充值些信仰
- CoorChice一直在不定期的分享新的干货,想要上车只需进到CoorChice的【个人主页】点个关注就好了哦。发车喽~