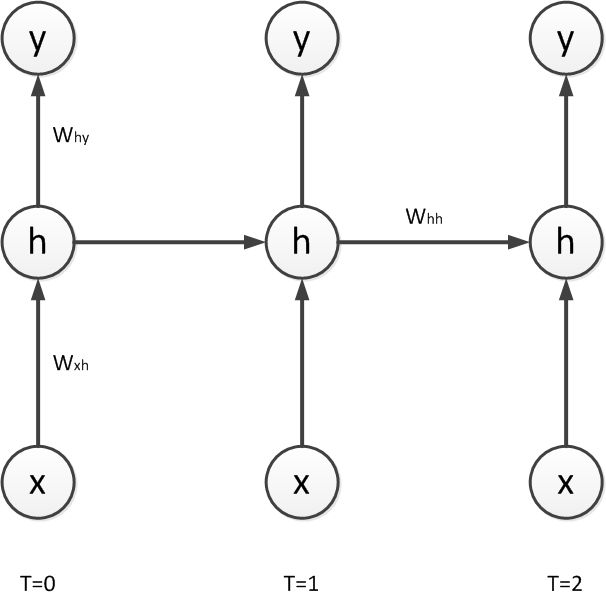
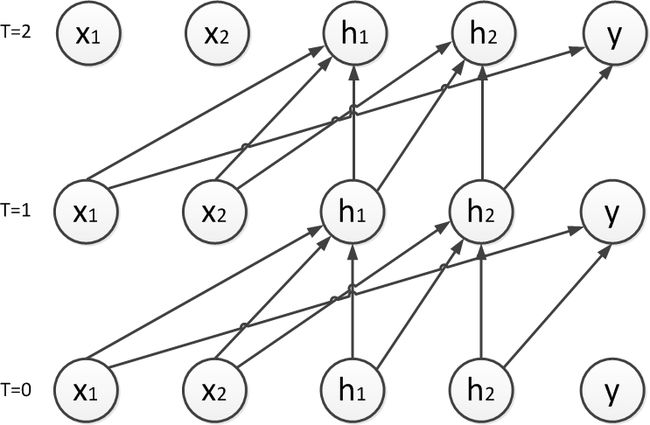
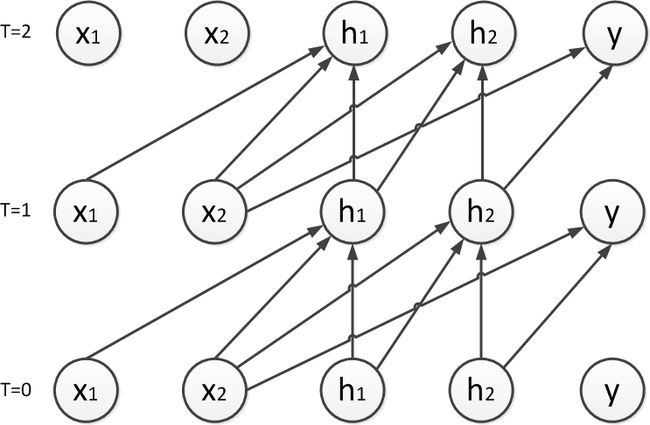
- 情绪觉察日记第37天
露露_e800
今天是家庭关系规划师的第二阶最后一天,慧萍老师帮我做了个案,帮我处理了埋在心底好多年的一份恐惧,并给了我深深的力量!这几天出来学习,爸妈过来婆家帮我带小孩,妈妈出于爱帮我收拾东西,并跟我先生和婆婆产生矛盾,妈妈觉得他们没有照顾好我…。今晚回家见到妈妈,我很欣赏她并赞扬她,妈妈说今晚要跟我睡我说好,当我们俩躺在床上准备睡觉的时候,我握着妈妈的手对她说:妈妈这几天辛苦你了,你看你多利害把我们的家收拾得
- 谢谢你们,爱你们!
鹿游儿
昨天家人去泡温泉,二个孩子也带着去,出发前一晚,匆匆下班,赶回家和孩子一起收拾。饭后,我拿出笔和本子(上次去澳门时做手帐的本子)写下了1\2\3\4\5\6\7\8\9,让后让小壹去思考,带什么出发去旅游呢?她在对应的数字旁边画上了,泳衣、泳圈、肖恩、内衣内裤、tapuy、拖鞋……画完后,就让她自己对着这个本子,将要带的,一一带上,没想到这次带的书还是这本《便便工厂》(晚上姑婆发照片过来,妹妹累得
- 向内而求
陈陈_19b4
10月27日,阴。阅读书目:《次第花开》。作者:希阿荣博堪布,是当今藏传佛家宁玛派最伟大的上师法王,如意宝晋美彭措仁波切颇具影响力的弟子之一。多年以来,赴海内外各地弘扬佛法,以正式授课、现场开示、发表文章等多种方法指导佛学弟子修行佛法。代表作《寂静之道》、《生命这出戏》、《透过佛法看世界》自出版以来一直是佛教类书籍中的畅销书。图片发自App金句:1.佛陀说,一切痛苦的根源在于我们长期以来对自身及外
- 高级编程--XML+socket练习题
masa010
java开发语言
1.北京华北2114.8万人上海华东2,500万人广州华南1292.68万人成都华西1417万人(1)使用dom4j将信息存入xml中(2)读取信息,并打印控制台(3)添加一个city节点与子节点(4)使用socketTCP协议编写服务端与客户端,客户端输入城市ID,服务器响应相应城市信息(5)使用socketTCP协议编写服务端与客户端,客户端要求用户输入city对象,服务端接收并使用dom4j
- 2018-07-23-催眠日作业-#不一样的31天#-66小鹿
小鹿_33
预言日:人总是在逃避命运的路上,与之不期而遇。心理学上有个著名的名词,叫做自证预言;经济学上也有一个很著名的定律叫做,墨菲定律;在灵修派上,还有一个很著名的法则,叫做吸引力法则。这3个领域的词,虽然看起来不太一样,但是他们都在告诉人们一个现象:你越担心什么,就越有可能会发生什么。同样的道理,你越想得到什么,就应该要积极地去创造什么。无论是自证预言,墨菲定律还是吸引力法则,对人都有正反2个维度的影响
- 2022-07-08
保利学府里李楚怡1307022
——保利碧桂园学府里——童梦奇趣【科学实验室】「7.9-7.10」✏玩出大智慧约99-144㎡二期全新升级力作
- 怎么起诉借钱不还的人?怎样起诉欠款不还的人?
影子爱学习
怎么起诉借钱不还的人?怎样起诉欠款不还的人?如果遇到难以解决的法律问题,我们可以匹配专业律师。例如:婚姻家庭(离婚纠纷)、刑事辩护、合同纠纷、债权债务、房产(继承)纠纷、交通事故、劳动争议、人身损害、公司相关法律事务(法律顾问)等咨询推荐手机/微信:15633770876【全国案件皆可】借钱不还起诉对方需要哪些资料起诉欠钱不还的,一般需要的材料包括以下这些:借据、收据、欠条、付款凭证等证据,以及向
- Goolge earth studio 进阶4——路径修改与平滑
陟彼高冈yu
Googleearthstudio进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径,所以当我们通过这个关键帧时,不是一个生硬的角度,而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄,允许我们调整路径的形状。右键单击,我们可以选择“平滑路径”,这是默认的自动平滑算法,或者我们可
- Python教程:一文了解使用Python处理XPath
旦莫
Python进阶python开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath?2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
- 509. 斐波那契数(每日一题)
lzyprime
lzyprime博客(github)创建时间:2021.01.04qq及邮箱:2383518170leetcode笔记题目描述斐波那契数,通常用F(n)表示,形成的序列称为斐波那契数列。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:F(0)=0,F(1)=1F(n)=F(n-1)+F(n-2),其中n>1给你n,请计算F(n)。示例1:输入:2输出:1解释:F(2)=F(1)+
- 18-115 一切思考不能有效转化为行动,都TM是扯淡!
成长时间线
7月25号写了一篇关于为什么会断更如此严重的反思,然而,之后日更仅仅维持了一周,又出现了这次更严重的现象。从8月2号到昨天8月6号,5天!又是5天没有更文!虽然这次断更时间和上次一样,那为什么说这次更严重?因为上次之后就分析了问题的原因,以及应该如何解决,按理说应该会好转,然而,没过几天严重断更的现象再次出现,想想,经过反思,问题依然没有解决与改变,这让我有些担忧。到底是哪里出了问题,难道我就真的
- 【华为OD机试真题2023B卷 JAVA&JS】We Are A Team
若博豆
java算法华为javascript
华为OD2023(B卷)机试题库全覆盖,刷题指南点这里WeAreATeam时间限制:1秒|内存限制:32768K|语言限制:不限题目描述:总共有n个人在机房,每个人有一个标号(1<=标号<=n),他们分成了多个团队,需要你根据收到的m条消息判定指定的两个人是否在一个团队中,具体的:1、消息构成为:abc,整数a、b分别代
- 2023-04-17|篮球女孩
长一木
1小学抑或初中阶段,在课外书了解到她的故事。“篮球女孩”。当时佩服她的顽强,也对生命多了一丝敬畏。今天刚好在公众号看到,长大后的“篮球女孩”。佩服之余又满是心疼。网络侵删祝那素未蒙面的女孩,未来一切顺遂。
- 398顺境,逆境
戴骁勇
2018.11.27周二雾霾最近儿子进入了一段顺境期,今天表现尤其不错。今天的数学测试成绩喜人,没有出现以往的计算错误,整个卷面书写工整,附加题也在规定时间内完成且做对。为迎接体育测试的锻炼有了质的飞跃。坐位体前屈成绩突飞猛进,估测成绩能达到12cm,这和上次测试的零分来比,简直是逆袭。儿子还在不断锻炼和提升,唯恐到时候掉链子。跑步姿势在我的调教下,逐渐正规起来,速度随之也有了提升。今晚测试的50
- python是什么意思中文-在python中%是什么意思
编程大乐趣
Python中%有两种:1、数值运算:%代表取模,返回除法的余数。如:>>>7%212、%操作符(字符串格式化,stringformatting),说明如下:%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+,-,''或0。+表示右对齐。-表示左对齐。''为一个空格,表示在正数的左侧填充一个空格,从而与负数对齐。0表示使用0填
- 2019-08-08
65454
东莞家庭聚会出行旅游去哪里玩住?想起来有很久没有和家里人聚会啦,这次组织家人来到威廉古堡别墅轰趴,一大家子27个人,在别墅订了一天办,玩的非常的开心,小孩子玩游戏机,也很放心不会丢,我们就在唱歌、打麻将、打桌球一系列的活动,还准备小次等小孩生日在别墅举办,还可以给孩子做一个生日的策划
- Day17笔记-高阶函数
~在杰难逃~
Python笔记python开发语言pycharm数据分析
高阶函数【重点掌握】函数的本质:函数是一个变量,函数名是一个变量名,一个函数可以作为另一个函数的参数或返回值使用如果A函数作为B函数的参数,B函数调用完成之后,会得到一个结果,则B函数被称为高阶函数常用的高阶函数:map(),reduce(),filter(),sorted()1.map()map(func,iterable),返回值是一个iterator【容器,迭代器】func:函数iterab
- python八股文面试题分享及解析(1)
Shawn________
python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果:21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型,不仅仅改变
- 【目标检测数据集】卡车数据集1073张VOC+YOLO格式
熬夜写代码的平头哥∰
目标检测YOLO人工智能
数据集格式:PascalVOC格式+YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件)图片数量(jpg文件个数):1073标注数量(xml文件个数):1073标注数量(txt文件个数):1073标注类别数:1标注类别名称:["truck"]每个类别标注的框数:truck框数=1120总框数:1120使用标注工具:labelImg标注
- 121. 买卖股票的最佳时机
薄荷糖的味道_fb40
给定一个数组,它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天(股票价格=1)的时候买入,在第5天(股票价格=6)的时候卖出,最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
- MYSQL面试系列-04
king01299
面试mysql面试
MYSQL面试系列-0417.关于redolog和binlog的刷盘机制、redolog、undolog作用、GTID是做什么的?innodb_flush_log_at_trx_commit及sync_binlog参数意义双117.1innodb_flush_log_at_trx_commit该变量定义了InnoDB在每次事务提交时,如何处理未刷入(flush)的重做日志信息(redolog)。它
- 【JS】执行时长(100分) |思路参考+代码解析(C++)
l939035548
JS算法数据结构c++
题目为了充分发挥GPU算力,需要尽可能多的将任务交给GPU执行,现在有一个任务数组,数组元素表示在这1秒内新增的任务个数且每秒都有新增任务。假设GPU最多一次执行n个任务,一次执行耗时1秒,在保证GPU不空闲情况下,最少需要多长时间执行完成。题目输入第一个参数为GPU一次最多执行的任务个数,取值范围[1,10000]第二个参数为任务数组长度,取值范围[1,10000]第三个参数为任务数组,数字范围
- 2022现在哪个打车软件比较好用又便宜 实惠的打车软件合集
高省APP珊珊
这是一个信息高速传播的社会。信息可以通过手机,微信,自媒体,抖音等方式进行传播。但同时这也是一个交通四通发达的社会。高省APP,是2022年推出的平台,0投资,0风险、高省APP佣金更高,模式更好,终端用户不流失。【高省】是一个自用省钱佣金高,分享推广赚钱多的平台,百度有几百万篇报道,也期待你的加入。珊珊导师,高省邀请码777777,注册送2皇冠会员,送万元推广大礼包,教你如何1年做到百万团队。高
- 似乎,发生了很多事情
阿皮Ponder
似乎,有很多事情正在发生。今天,我跟夫人陪着孩子走进来幼儿园,人生头一回以孩子家长的身份参加了小小的班级家长会。在幼儿园,遇见老同学。从2017年开始失联,因为对方遇到了一些事情,跟大家都失去了联系,今日再见面,分外激动,他拉着我一直聊,一直聊。感谢我们的孩子。孩子有点咳嗽,去医院做了检查。叔叔家的两个妹妹开始了高中生活,新的开始。过去看望,遇到一位老师,很是面熟。咨询之下,果然,曾经初中母校的老
- 2022-11-17
无奇君
又去了一次社康,这次是急性支气管炎……太难了。半夜就猛咳,天天咳醒,还好他戴海绵耳塞睡吵不到他,要不然对他来说也是种煎熬。一累也会猛咳,希望这次是最后一次吃药,吃完就好。又想把头发剪短了,顺便染个色。可是刚刚去看人家还没开门,不是休息日老板好佛系。理发店是个夫妻店,一年多前刚搬来的时候老板还没对象呢,当时聊天老板就说希望能找个对象一起两个人守着店都比上班强。不久后再去他已经有对象了,而且在店里帮忙
- 嘿,谢谢你
小小玛拉沁
突然想对一个女孩子说,谢谢你!很久很久以前,总是觉得和你不会有太多交集,充其量也只是普通的舍友吧,毕竟有很多习惯,性格等方面相差甚远。其实特别感谢2017这一段经历和我遇见的人,只会慢吞吞的过自己生活的安小蜗是不会主动去结交朋友的,所以她来到了我的世界,让我在不知不觉中发现了自己太多太多的问题,而我正在逐渐去改变这些的习惯,成为更好的自己!我总是超级佩服她不管什么时候精力都超级旺盛,可以在上了一天
- 【华为OD技术面试真题 - 技术面】- python八股文真题题库(4)
算法大师
华为od面试python
华为OD面试真题精选专栏:华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例:文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片(Slicing)操作**基本切片语法
- 第六集如何安装CentOS7.0,3分钟学会centos7安装教程
date分享
从光盘引导系统按回车键继续进入引导程序安装界面,选择语言这里选择简体中文版点击继续选择桌面安装下面给系统分区选择磁盘,点击完成选择基本分区,点击加号swap分区,大小填内存的两倍在选择根分区,使用所有可用的磁盘空间选择文件系统ext4点击完成,点击开始安装设置root密码,点击完成设置普通用户和密码,点击完成整个过程持续八分钟左右根据个人配置不同,时间长短不同好,现在点击重启系统进入重启状态点击本
- 23.3.27精进
07439acfb561
落地真经严格就是爱,放纵既是害正能量语录每一颗螺丝都有标准每一颗螺丝都是标维今日体验不要质疑你的付出,这些都会是一种积累,一种沉淀,它们会默默的铺路,只为让你成为更优秀的人。
- Python爬虫解析工具之xpath使用详解
eqa11
python爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中,数据提取是一个至关重要的环节。xpath作为一门
- 戴尔笔记本win8系统改装win7系统
sophia天雪
win7戴尔改装系统win8
戴尔win8 系统改装win7 系统详述
第一步:使用U盘制作虚拟光驱:
1)下载安装UltraISO:注册码可以在网上搜索。
2)启动UltraISO,点击“文件”—》“打开”按钮,打开已经准备好的ISO镜像文
- BeanUtils.copyProperties使用笔记
bylijinnan
java
BeanUtils.copyProperties VS PropertyUtils.copyProperties
两者最大的区别是:
BeanUtils.copyProperties会进行类型转换,而PropertyUtils.copyProperties不会。
既然进行了类型转换,那BeanUtils.copyProperties的速度比不上PropertyUtils.copyProp
- MyEclipse中文乱码问题
0624chenhong
MyEclipse
一、设置新建常见文件的默认编码格式,也就是文件保存的格式。
在不对MyEclipse进行设置的时候,默认保存文件的编码,一般跟简体中文操作系统(如windows2000,windowsXP)的编码一致,即GBK。
在简体中文系统下,ANSI 编码代表 GBK编码;在日文操作系统下,ANSI 编码代表 JIS 编码。
Window-->Preferences-->General -
- 发送邮件
不懂事的小屁孩
send email
import org.apache.commons.mail.EmailAttachment;
import org.apache.commons.mail.EmailException;
import org.apache.commons.mail.HtmlEmail;
import org.apache.commons.mail.MultiPartEmail;
- 动画合集
换个号韩国红果果
htmlcss
动画 指一种样式变为另一种样式 keyframes应当始终定义0 100 过程
1 transition 制作鼠标滑过图片时的放大效果
css
.wrap{
width: 340px;height: 340px;
position: absolute;
top: 30%;
left: 20%;
overflow: hidden;
bor
- 网络最常见的攻击方式竟然是SQL注入
蓝儿唯美
sql注入
NTT研究表明,尽管SQL注入(SQLi)型攻击记录详尽且为人熟知,但目前网络应用程序仍然是SQLi攻击的重灾区。
信息安全和风险管理公司NTTCom Security发布的《2015全球智能威胁风险报告》表明,目前黑客攻击网络应用程序方式中最流行的,要数SQLi攻击。报告对去年发生的60亿攻击 行为进行分析,指出SQLi攻击是最常见的网络应用程序攻击方式。全球网络应用程序攻击中,SQLi攻击占
- java笔记2
a-john
java
类的封装:
1,java中,对象就是一个封装体。封装是把对象的属性和服务结合成一个独立的的单位。并尽可能隐藏对象的内部细节(尤其是私有数据)
2,目的:使对象以外的部分不能随意存取对象的内部数据(如属性),从而使软件错误能够局部化,减少差错和排错的难度。
3,简单来说,“隐藏属性、方法或实现细节的过程”称为——封装。
4,封装的特性:
4.1设置
- [Andengine]Error:can't creat bitmap form path “gfx/xxx.xxx”
aijuans
学习Android遇到的错误
最开始遇到这个错误是很早以前了,以前也没注意,只当是一个不理解的bug,因为所有的texture,textureregion都没有问题,但是就是提示错误。
昨天和美工要图片,本来是要背景透明的png格式,可是她却给了我一个jpg的。说明了之后她说没法改,因为没有png这个保存选项。
我就看了一下,和她要了psd的文件,还好我有一点
- 自己写的一个繁体到简体的转换程序
asialee
java转换繁体filter简体
今天调研一个任务,基于java的filter实现繁体到简体的转换,于是写了一个demo,给各位博友奉上,欢迎批评指正。
实现的思路是重载request的调取参数的几个方法,然后做下转换。
- android意图和意图监听器技术
百合不是茶
android显示意图隐式意图意图监听器
Intent是在activity之间传递数据;Intent的传递分为显示传递和隐式传递
显式意图:调用Intent.setComponent() 或 Intent.setClassName() 或 Intent.setClass()方法明确指定了组件名的Intent为显式意图,显式意图明确指定了Intent应该传递给哪个组件。
隐式意图;不指明调用的名称,根据设
- spring3中新增的@value注解
bijian1013
javaspring@Value
在spring 3.0中,可以通过使用@value,对一些如xxx.properties文件中的文件,进行键值对的注入,例子如下:
1.首先在applicationContext.xml中加入:
<beans xmlns="http://www.springframework.
- Jboss启用CXF日志
sunjing
logjbossCXF
1. 在standalone.xml配置文件中添加system-properties:
<system-properties> <property name="org.apache.cxf.logging.enabled" value=&
- 【Hadoop三】Centos7_x86_64部署Hadoop集群之编译Hadoop源代码
bit1129
centos
编译必需的软件
Firebugs3.0.0
Maven3.2.3
Ant
JDK1.7.0_67
protobuf-2.5.0
Hadoop 2.5.2源码包
Firebugs3.0.0
http://sourceforge.jp/projects/sfnet_findbug
- struts2验证框架的使用和扩展
白糖_
框架xmlbeanstruts正则表达式
struts2能够对前台提交的表单数据进行输入有效性校验,通常有两种方式:
1、在Action类中通过validatexx方法验证,这种方式很简单,在此不再赘述;
2、通过编写xx-validation.xml文件执行表单验证,当用户提交表单请求后,struts会优先执行xml文件,如果校验不通过是不会让请求访问指定action的。
本文介绍一下struts2通过xml文件进行校验的方法并说
- 记录-感悟
braveCS
感悟
再翻翻以前写的感悟,有时会发现自己很幼稚,也会让自己找回初心。
2015-1-11 1. 能在工作之余学习感兴趣的东西已经很幸福了;
2. 要改变自己,不能这样一直在原来区域,要突破安全区舒适区,才能提高自己,往好的方面发展;
3. 多反省多思考;要会用工具,而不是变成工具的奴隶;
4. 一天内集中一个定长时间段看最新资讯和偏流式博
- 编程之美-数组中最长递增子序列
bylijinnan
编程之美
import java.util.Arrays;
import java.util.Random;
public class LongestAccendingSubSequence {
/**
* 编程之美 数组中最长递增子序列
* 书上的解法容易理解
* 另一方法书上没有提到的是,可以将数组排序(由小到大)得到新的数组,
* 然后求排序后的数组与原数
- 读书笔记5
chengxuyuancsdn
重复提交struts2的token验证
1、重复提交
2、struts2的token验证
3、用response返回xml时的注意
1、重复提交
(1)应用场景
(1-1)点击提交按钮两次。
(1-2)使用浏览器后退按钮重复之前的操作,导致重复提交表单。
(1-3)刷新页面
(1-4)使用浏览器历史记录重复提交表单。
(1-5)浏览器重复的 HTTP 请求。
(2)解决方法
(2-1)禁掉提交按钮
(2-2)
- [时空与探索]全球联合进行第二次费城实验的可能性
comsci
二次世界大战前后,由爱因斯坦参加的一次在海军舰艇上进行的物理学实验 -费城实验
至今给我们大家留下很多迷团.....
关于费城实验的详细过程,大家可以在网络上搜索一下,我这里就不详细描述了
在这里,我的意思是,现在
- easy connect 之 ORA-12154: TNS: 无法解析指定的连接标识符
daizj
oracleORA-12154
用easy connect连接出现“tns无法解析指定的连接标示符”的错误,如下:
C:\Users\Administrator>sqlplus username/
[email protected]:1521/orcl
SQL*Plus: Release 10.2.0.1.0 – Production on 星期一 5月 21 18:16:20 2012
Copyright (c) 198
- 简单排序:归并排序
dieslrae
归并排序
public void mergeSort(int[] array){
int temp = array.length/2;
if(temp == 0){
return;
}
int[] a = new int[temp];
int
- C语言中字符串的\0和空格
dcj3sjt126com
c
\0 为字符串结束符,比如说:
abcd (空格)cdefg;
存入数组时,空格作为一个字符占有一个字节的空间,我们
- 解决Composer国内速度慢的办法
dcj3sjt126com
Composer
用法:
有两种方式启用本镜像服务:
1 将以下配置信息添加到 Composer 的配置文件 config.json 中(系统全局配置)。见“例1”
2 将以下配置信息添加到你的项目的 composer.json 文件中(针对单个项目配置)。见“例2”
为了避免安装包的时候都要执行两次查询,切记要添加禁用 packagist 的设置,如下 1 2 3 4 5
- 高效可伸缩的结果缓存
shuizhaosi888
高效可伸缩的结果缓存
/**
* 要执行的算法,返回结果v
*/
public interface Computable<A, V> {
public V comput(final A arg);
}
/**
* 用于缓存数据
*/
public class Memoizer<A, V> implements Computable<A,
- 三点定位的算法
haoningabc
c算法
三点定位,
已知a,b,c三个顶点的x,y坐标
和三个点都z坐标的距离,la,lb,lc
求z点的坐标
原理就是围绕a,b,c 三个点画圆,三个圆焦点的部分就是所求
但是,由于三个点的距离可能不准,不一定会有结果,
所以是三个圆环的焦点,环的宽度开始为0,没有取到则加1
运行
gcc -lm test.c
test.c代码如下
#include "stdi
- epoll使用详解
jimmee
clinux服务端编程epoll
epoll - I/O event notification facility在linux的网络编程中,很长的时间都在使用select来做事件触发。在linux新的内核中,有了一种替换它的机制,就是epoll。相比于select,epoll最大的好处在于它不会随着监听fd数目的增长而降低效率。因为在内核中的select实现中,它是采用轮询来处理的,轮询的fd数目越多,自然耗时越多。并且,在linu
- Hibernate对Enum的映射的基本使用方法
linzx0212
enumHibernate
枚举
/**
* 性别枚举
*/
public enum Gender {
MALE(0), FEMALE(1), OTHER(2);
private Gender(int i) {
this.i = i;
}
private int i;
public int getI
- 第10章 高级事件(下)
onestopweb
事件
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- 孙子兵法
roadrunners
孙子兵法
始计第一
孙子曰:
兵者,国之大事,死生之地,存亡之道,不可不察也。
故经之以五事,校之以计,而索其情:一曰道,二曰天,三曰地,四曰将,五
曰法。道者,令民于上同意,可与之死,可与之生,而不危也;天者,阴阳、寒暑
、时制也;地者,远近、险易、广狭、死生也;将者,智、信、仁、勇、严也;法
者,曲制、官道、主用也。凡此五者,将莫不闻,知之者胜,不知之者不胜。故校
之以计,而索其情,曰
- MySQL双向复制
tomcat_oracle
mysql
本文包括:
主机配置
从机配置
建立主-从复制
建立双向复制
背景
按照以下简单的步骤:
参考一下:
在机器A配置主机(192.168.1.30)
在机器B配置从机(192.168.1.29)
我们可以使用下面的步骤来实现这一点
步骤1:机器A设置主机
在主机中打开配置文件 ,
- zoj 3822 Domination(dp)
阿尔萨斯
Mina
题目链接:zoj 3822 Domination
题目大意:给定一个N∗M的棋盘,每次任选一个位置放置一枚棋子,直到每行每列上都至少有一枚棋子,问放置棋子个数的期望。
解题思路:大白书上概率那一张有一道类似的题目,但是因为时间比较久了,还是稍微想了一下。dp[i][j][k]表示i行j列上均有至少一枚棋子,并且消耗k步的概率(k≤i∗j),因为放置在i+1~n上等价与放在i+1行上,同理