|
Flip Game
Description
Flip game is played on a rectangular 4x4 field with two-sided pieces placed on each of its 16 squares. One side of each piece is white and the other one is black and each piece is lying either it's black or white side up. Each round you flip 3 to 5 pieces, thus changing the color of their upper side from black to white and vice versa. The pieces to be flipped are chosen every round according to the following rules:
 Consider the following position as an example:
bwbw wwww bbwb bwwb Here "b" denotes pieces lying their black side up and "w" denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become: bwbw bwww wwwb wwwb The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal. Input
The input consists of 4 lines with 4 characters "w" or "b" each that denote game field position.
Output
Write to the output file a single integer number - the minimum number of rounds needed to achieve the goal of the game from the given position. If the goal is initially achieved, then write 0. If it's impossible to achieve the goal, then write the word "Impossible" (without quotes).
Sample Input bwwb
bbwb
bwwb
bwww Sample Output 4
Source
Northeastern Europe 2000
|
题目大意：
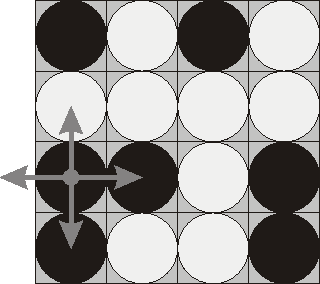
有$4\times 4$的棋盘，上面的棋子一面是黑的，一面是白的。规定翻转一个棋子的同时也要翻转它的上、下、左、右的棋子，问给定一个棋盘的棋子状态，至少需要翻转多少个棋子，能使得所有棋子都是白的或黑的（面在上）。
基本思路：
一、暴力搜索出奇迹：
1、首先要明确一点：这个翻棋子就像按位异或一样，如果一列数里面有两个数是相等的，那把它们全都异或起来，根据结合率就相当于在这过程中有一个数与自身异或，结果为0。把这两个相等的数去掉对最终异或结果是没有影响的。同样看这个翻棋子，它只有两个面，翻一次由黑面在上转为白面在上，或者白转黑，但翻两次就恢复原来的样子了，翻没翻是一样的，除非再翻多一次，甚至是奇数次，但这没有必要也没有意义。
2、数据规模小，考虑我们最少不翻任何棋子（初始状态就是全白或全黑），最多只翻16个棋子（再翻就有棋子被翻两次了），因此总的状态数为$C^{0}_{16}+C^{1}_{16}+\cdots+C^{16}_{16}=2^{16}$，直接枚举或搜索即可。
3、考虑要求的是最小值，因此从翻$0$个开始，搜索翻$i$个，直到翻$16$个，中间搜索到即为最小值，翻16个都不满足即输出$Impossible$。
4、由于棋子都只有黑、白两面，可以用0、1表示，因此可以位压缩成一个数字来进行判断，翻棋子的操作可使用位运算，有两种方法：
方法一：每一行压缩一个数字，对第$i$行第$j$列棋子进行翻转，比如$j=2$，则$i-1$、$i+1$行的棋子应该和4（0100）相异或（与1异或切换状态，与0异或不改变），而第$i$行棋子应与14（1110）相异或。
方法二：只有16个棋子，一个int型变量就能存下这16个0/1了，所以可以直接压缩成一个数字。如$i=2, j=2$，则与20032（0100 1110 0100 0000）相异或，不过手算16位的状态是比手算4位烦一点点。
5、搜索过程中要注意搜过的位置不需要再搜了，所以在函数里控制一下$i$、$j$，当然实现并不唯一。还要注意如果没搜成功，把棋子再翻（flip）一遍，这样就能恢复原样了。不需要memcpy，那是很蠢的做法。
方法一代码：
1 #include
2
3 int field[6]={0};
4 int state[][4]={{8,4,2,1},{12,14,7,3}};
5
6 void read() {
7 for(int i=1; i<=4; i++) {
8 for(int j=1; j<=4; j++) {
9 field[i]<<=1;
10 if(getchar()=='b')
11 field[i]|=1;
12 }
13 getchar();
14 }
15 }
16
17 void flip(int i, int j) {--j;
18 field[i-1]^=state[0][j];
19 field[i] ^=state[1][j];
20 field[i+1]^=state[0][j];
21 }
22
23 bool check() {
24 return (field[1]==0||field[1]==15)
25 && field[1]==field[2]
26 && field[2]==field[3]
27 && field[3]==field[4];
28 }
29
30 bool find(int n, int i, int j) {
31 if(n==0) return check();
32 j+=1; if(j>4) i+=1, j=1;
33 if(i>4) return false;
34 for(; i<=4; i++) {
35 for(; j<=4; j++) {
36 flip(i, j);
37 if(find(n-1,i,j))
38 return true;
39 flip(i, j);
40 }
41 j=1;
42 }
43 return false;
44 }
45
46 void work() {
47 for(int i=0; i<=16; i++)
48 if(find(i,1,0)) {
49 printf("%d\n", i);
50 return;
51 }
52 puts("Impossible");
53 }
54
55 int main() {
56 read();
57 work();
58 return 0;
59 }
方法二代码（首先打个表）：
1 void init() {
2 for(int i=1; i<=16; i++) {
3 int v=0, k=1<<(i-1); v|=k;
4 if((i+1)%4!=1) v|=k<<1;
5 if((i-1)%4!=0) v|=k>>1;
6 if(i>4) v|=k>>4;
7 if(i<13) v|=k<<4;
8 printf("%d,",v);
9 }
10 }
然后就可以拿表去水了，当然直接判断也是可以的，丑。
1 #include
2
3 int field;
4 int state[]={19,39,78,140,305,626,1252,2248,4880,10016,20032,35968,12544,29184,58368,51200};
5
6 void read() {
7 for(int i=0; i<4; i++) {
8 for(int j=0; j<4; j++) {
9 field<<=1;
10 if(getchar()=='b')
11 field|=1;
12 }
13 getchar();
14 }
15 }
16
17 void flip(int i) {
18 field^=state[i];
19 }
20
21 bool check() {
22 return field==0x0000||field==0xFFFF;
23 }
24
25 bool find(int n, int i) {
26 if(n==0) return check();
27 //if(i>=16) return false;
28 for(; i<16; i++) {
29 flip(i);
30 if(find(n-1,i+1))
31 return true;
32 flip(i);
33 }
34 return false;
35 }
36
37 void work() {
38 for(int c=0; c<=16; c++)
39 if(find(c,0)) {
40 printf("%d\n", c);
41 return;
42 }
43 puts("Impossible");
44 }
45
46 int main() {
47 read();
48 work();
49 return 0;
50 }
二、枚举
1、这题应该容易想搜索，当然枚举也是比较简单能想到的。我们还是像前面方法二那样位压缩成一个数，如果不能压成一个int的话这题当然也用不了枚举。需要考虑的是如何实现$C^i_{16}$，也就是$16$个选$i$个$(i\in [0, 16])$，考虑我选哪几个棋子也表示成0/1，选择翻转的棋子我用1表示，比如要选择第1个、第3个、第5个和第6个，那就是11 0101的状态。这样枚举就很方便了，枚举值范围0x0000～0xFFFF。
2、同样像上面方法二那样打个表，对于每个枚举的状态，用位与运算求出哪个位是1（哪个棋子要翻转），然后根据打表的数据对输入的棋盘进行异或运算。过程中对翻转后棋盘全黑或全白的情况求最少翻转数。
3、可以顺手再打 1<<0 ~ 1<<15 的表。
1 #include
2
3 int field;
4 int state[]={19,39,78,140,305,626,1252,2248,4880,10016,20032,35968,12544,29184,58368,51200};
5 int bit[]={1,2,4,8,16,32,64,128,256,512,1024,2048,4096,8192,16384,32768};
6
7 void read() {
8 for(int i=0; i<4; i++) {
9 for(int j=0; j<4; j++) {
10 field<<=1;
11 if(getchar()=='b')
12 field|=1;
13 }
14 getchar();
15 }
16 }
17
18 bool check() {
19 return field==0x0000||field==0xFFFF;
20 }
21
22 int minn=0xFF;
23 void work() {
24 for(int flip=0; flip<=0xFFFF; flip++) {
25 int temp=field, cnt=0;
26 for(int i=0; i<16; i++)
27 if(flip&bit[i]) {// flip&(1<
28 field^=state[i];
29 ++cnt;
30 }
31 if(check()&&minn>cnt) minn=cnt;
32 field=temp;
33 }
34 }
35
36 void print() {
37 if(minn==0xFF) puts("Impossible");
38 else printf("%d\n", minn);
39 }
40
41 int main() {
42 read();
43 work();
44 print();
45 return 0;
46 }
三、高斯消元法
1、基本想法是，令a=棋盘状态矩阵，b=最终各棋子的状态，ax=b解出x=要翻转的棋子，数一下x里面1的数量就是翻转的棋子数了。因为最终状态可以是全黑或全白，因此需要对b取两次值，做两次消元。
2、但是你会发现，这题会经常出现无穷多解的情况，也就是存在自由变元。因此需要枚举or搜索这些自由变元的值。
（代码目前没交，待更新）
——原创by BlackStorm，转载请注明出处。
本文地址：http://www.cnblogs.com/BlackStorm/p/5231470.html