二分类Logistic回归模型

　　Logistic回归属于概率型的非线性回归，分为二分类和多分类的回归模型。这里只讲二分类。

　　对于二分类的Logistic回归，因变量y只有“是、否”两个取值，记为1和0。这种值为0/1的二值品质型变量，我们称其为二分类变量。

　　假设在自变量$x_{1}, x_{2}, \cdots, x_{p}$作用下，y取“是”的概率是p，则取“否”的概率是1-p，研究的是当y取“是”发生的模率p与自变量$x_{1}, x_{2}, \cdots, x_{p}$的关系。

Logistic回归模型

①Logit变换

　　Logit 变换以前用于人口学领域，1970年被Cox引入来解决曲线直线化问题。

　　通常把某种结果出现的概率与不出现的概率之比称为称为事件的优势比odds，即假设在p个独立自变量$x_{1}, x_{2}, \cdots, x_{p}$作用下，记y取1的概率是$p=P(y=1 | X)$，取0概率是$1-p$，取1和取0的概率之比为$\frac{p}{1-p}$。Logit变换即取对数：$$\lambda  = \ln ({\rm{ odds }}) = \ln \frac{p}{{1 - p}}$$

②Logistic函数

　　Logistic中文意思为“逻辑”，但是这里，并不是逻辑的意思，而是通过logit变换来命名的。

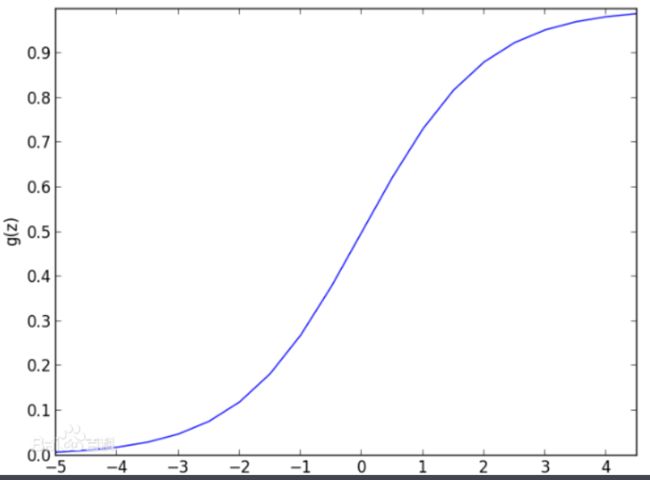
　　二元logistic回归是指因变量为二分类变量的回归分析，目标概率的取值会在0~1之间，但是回归方程的因变量取值却落在实数集当中，这个是不能够接受的，所以，可以先将目标概率做Logit变换，这样它的取值区间变成了整个实数集，采用这种处理方法的回归分析，就是Logistic回归。Logistic函数为：

$$\operatorname{Logit}(p)=\ln \left(\frac{p}{1-p}\right)=Z，p=\frac{1}{1+\mathrm{e}^{-2}}$$

　　

　　Logistic回归模型中的因变量只有1和0（如是和否、发生和不发生）两种取值。对odds取自然对数即得Logistic变换$\operatorname{Logit}(p)=\ln \left(\frac{p}{1-p}\right) A$。

　　当p在(0，1)之间变化时，odds的取值范围是(0，+oo)，则Logistic函数的取值范围是(-oo，+oo)。

③Logistic回归模型

　　Logistic 回归模型是建立$\ln \left(\frac{p}{1-p}\right)$与自然变量的线性回归模型。

　　Logistic 回归模型的公式为：$$\ln \left(\frac{p}{1-p}\right)=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{p} x_{p}+\varepsilon$$

　　因为$\ln \left(\frac{p}{1-p}\right)$的取值范围是(-oo，+oo)，这样，自变量$x_{1}, x_{2}, \cdots, x_{p}$可在任意范围内取值。

　　记$g(x)=\beta_{0}+\beta_{1} x_{1}+\dots+\beta_{p} x_{p}$，得到：$$\begin{array}{c}{p=P(y=1 | X)=\frac{1}{1+e^{-\mathrm{g}(x)}}} \\ {1-p=P(y=0 | X)=1-\frac{1}{1+e^{-\mathrm{g}(x)}}=\frac{1}{1+e^{\mathrm{g}(\mathrm{x})}}}\end{array}$$

　　解释：$$\frac{p}{1-p}=e^{\beta_{0}+\beta_{1}x_{1}+\ldots+\beta_\mathrm{p}x_{p} +\varepsilon}$$

　　其中，$\beta_{0}$为在没有自变量，即$x_{1}, x_{2}, \cdots, x_{p}$全部取0，y=1与y=0发生概率之比的自然对数。

　　$\beta_{i}$为某自变量x变化时，即x=1与x=0相比，y=1优势比的对数值。

 

和列联表、最小二乘法的区别

和列联表区别

　　对于分类资料的分析，当要考察的影响因素较少，且也为分类变量时，分析者常用列联表的形式对这种资料进行整理，并使用卡方检验来进行分析。

　　局限性：

　　①无法描述其作用大小及方向，更不能考察各因素间是否存在交互作用；

　　②该方法对样本含量的要求较大，当控制的分层因素较多时，单元格被划分的越来越细，列联表的格子中频数可能很小，将导致检验结果的不可靠。

　　③卡方检验无法对连续性自变量的影响进行分析，而这将大大限制其应用范围。

和最小二乘法区别

　　①取值区间：上述模型进行预报的范围为整个实数集，而模型左边的取值范围为0≤Ps1，二者并不相符。模型本身不能保证在自变量的各种组合下，因变量的估计值仍限制在0~1内。

　　②曲线关联：根据大量的观察，反应变量P与自变量的关系通常不是直线关系，而是S型曲线关系。显然，线性关联是线性回归中至关重要的一个前提假设，而在上述模型中这一假设是明显无法满足的。

 

建模步骤与MATLAB实现

步骤：

　　①根据挖掘的目的设置指标变量：$y, x_{1}, x_{2}, \cdots, x_{p}$。

　　②列出回归方程：$$\ln \left(\frac{p}{1-p}\right)=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{p} x_{p}+\varepsilon$$

　　③用$\ln \left(\frac{p}{1-p}\right)$和自变量列出线性回归方程，估计回归系数。

　　④模型检验——F检验，应用方差分析表对模型进行F检验。

　　根据输出的方差分析表中的F值和p值来检验该回归方程是否显著，如果p值小于显著性水平a则模型通过检验，可以进行下一步回归系数的检验；否则要重新选择指标变量，重新建立回归方程。

　　⑤回归系数检验——t检验，应用参数估计表对回归系数进行t检验。

　　在多元线性回归中，回归方程显著并不意味着每个自变量对y的影响都显著，为了从回归方程中剔除那些次要的、可有可无的变量，重新建立更为简单有效的回归方程，需要对每个自变量进行显著性检验，检验结果由参数估计表得到，采用逐步回归法，首先剔除掉最不显著的因变量，重新构造回归方程，一直到模型和参与的回归系数都通过检验；

　　⑥预测控制。

　　 

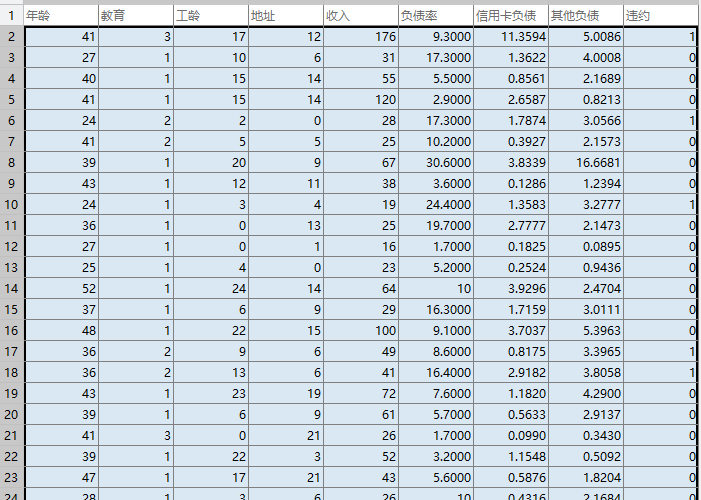
　　利用MATLAB对银行贷款拖欠率数据进行逻辑回归分析，分别采用逐步寻优（逐步剔除掉最不显著的因变量）和使用MATLAB自带的逐步向前、向后回归函数进行建模。

%% 逻辑回归 自动建模
clear;
% 参数初始化
filename = '../data/bankloan.xls' ; 
%% 读取数据
[num,txt] = xlsread(filename);
X = num(:,1:end-1);
Y = num(:,end);
%% 递归建模 
flag =1;
mdl = fitglm(X,Y,'linear','distr','binomial','Link','logit');
while flag ==1
    disp(mdl); % 打印model
    pValue = mdl.Coefficients.pValue;
    pValue_gt05 =pValue>0.05 ;
    if sum(pValue_gt05)==0 % 没有pValue值大于0.05的值
       flag =0;
       break;
    end
    % 移除pValue中大于0.05的变量最大的变量
    fprintf('\n移除变量：');
    [t,index]= max(pValue,[],1);
    fprintf('%s\t',mdl.CoefficientNames{1,index});
    fprintf('\n模型如下：');
    if index-1~=0   
        removeVariance =mdl.CoefficientNames{1,index};
    else
        removeVariance ='1';
    end
        % 从模型中移除变量
    mdl = removeTerms(mdl,removeVariance);
end
%% 自动建模 ，添加变量
disp('添加变量，自动建模中...');
mdl2 = stepwiseglm(X,Y,'constant','Distribution','binomial','Link','logit');
disp('添加变量，自动建模模型如下：')
disp(mdl2);
%% 自动建模 ， 移除变量
disp('移除变量，自动建模中...');
mdl3 =stepwiseglm(X,Y,'linear','Distribution','binomial','Link','logit');
disp('移除变量，自动建模模型如下：')
disp(mdl3);