树是一种很重要的数据结构,二叉树 、 AVL树 、红黑树 、 2-3树 、B-Tree 、B+Tree
==== 二叉 树 ====
定义:
- 若它的左子树不为空,则左子树上所有结点的值均小于等于根结点的值;
- 若它的右子树不为空,则右子树上所有结点的值均大于等于根结点的值;
- 它的左右子树均为二分查找树。
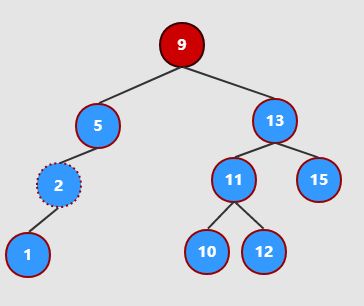
选取一个节点为参照根节点,会发现所有的左侧子节点小于等于参照点,右侧大于等于参照点。
比如根节点9, 9所有的左侧子节点(5、2、7、1、3)都小于等于9.
比如根节点13,13所有的左侧子节点(11、10、12)都大于等于13.
1、查找
查找节点 10:根节点9开始,10>9 右侧,10<13 左侧,10<11 左侧,找到10.
2、插入
插入 子节点 4:4<9 左侧,4<5 左侧,4>2 右侧,4>3 右侧
3、删除
删除节点(因为情况有多种,处理逻辑也是比较麻烦。)
A:删除叶子:好吧就是一个干巴巴的叶子,好办,找到-删除。
删除 7 ,这个7是叶子,那就找到并删除
B:有一个分支的,删除节点,子节点上提。
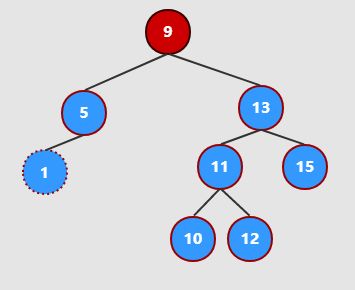
删除 2节点:找到2 ,删除2
再上提子节点 1
C:两个分支,节点删除,右子树最小的数代替被删除节点,
因为右子树最多有一个右叶子,重新指定引用。
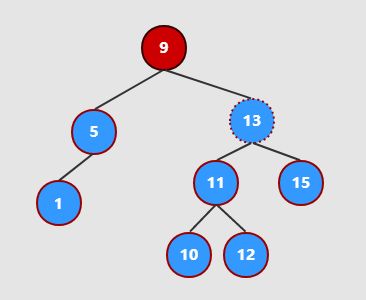
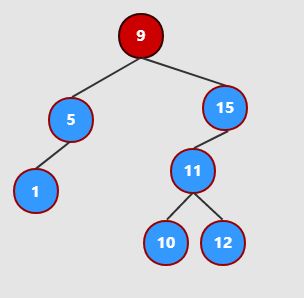
删除 13,13有左右两个分支:
因为 右分支肯定大于左面分支,所以上提右子节点 15
==== AVL 树 ====
自平衡二叉树,任一节点对应的两棵子树的最大高度差为1。也可以称之为 高度平衡树。
插入、查询、删除平均最坏的时间复杂度为O( log n )。
每个节点都有一个平衡因子,即左右子树的高度差 0 ,1,-1 这是满足AVL树的条件的;
也有可能是 -2 或者 2,高度差>1,所以需要自己再平衡,来满足AVL树的条件。
也就是只要高度大于1我就会自己执行执行一下旋转:
有这4种情况:左左 左右 右右 右左
左左:右旋转(单旋转)
左右:左旋转+右旋转(双旋转)
右右:左旋转(单旋转)
右左:左旋转+右旋转(双旋转),达到平衡
以上对应的是插入操作
查找:同二叉树
删除:父节点的平衡因子依然维护在 0 ,1 ,-1 说明没有打破平衡。平衡因子 2或者-2,我们依然使用旋转来达到平衡。