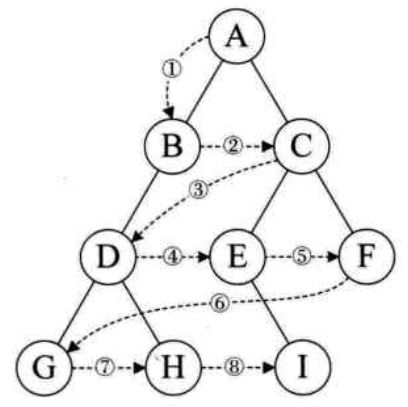
树的遍历,是指依照一定的规律不反复地訪问(或取出节点中的信息,或对节点做其它的处理)树中的每个节点,遍历是将非线性的树状结构按一定规律转化为线性结构。
1. 多叉树遍历
多叉树遍历分为深度优先遍历和广度优先遍历两类。树孩子表示法比较容易遍历。
图形演示:visualgo DFS BFS
1.1 深度优先遍历(DFS:Depth First Search)
深度优先遍历:从根节点开始先沿着树的一个枝遍历到叶子节点,再遍历其他的枝。深度优先遍历又分为先序遍历和后序遍历。
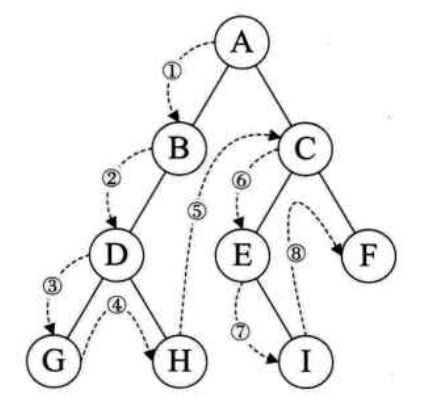
1.1.1 先序遍历
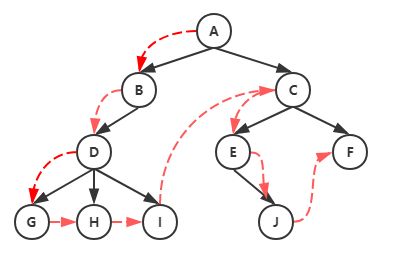
树中父节点先于子节点访问
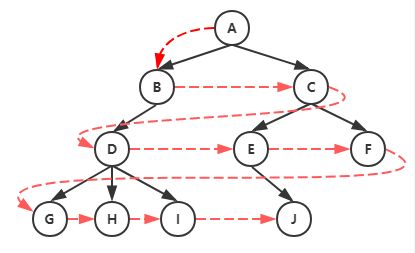
上图树的先序遍历结果:A → B → D → G → H → I → C → E → J → F
通常先序遍历实现分两种方式:递归方式和非递归方式(栈方式)。
参考代码
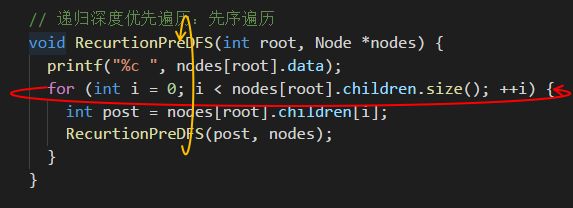
递归深度优先遍历:先序遍历
void RecurtionPreDFS(int root,Node* nodes){
printf("%c ",nodes[root].data);
for(int i= 0;i非递归深度优先遍历:先序遍历
void PreDFS(int root,Node* nodes){
stack s;
s.push(root);
while(!s.empty()){
int now = s.top();
s.pop();
printf("%c ",nodes[now].data);// 出栈访问
for(int i= nodes[now].children.size()-1; i>=0;--i){
int post = nodes[now].children[i];
s.push(post);
}
}
}
迭代是横向思维,递归是纵向思维
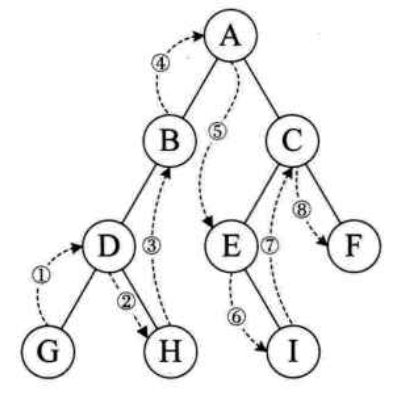
1.1.2 后序遍历
树中子节点先于父节点访问
上图树的后序遍历结果:G → H → I → D → B → J → E → F → C → A
递归深度优先遍历:后序遍历
void RecurtionPostDFS(int root,Node* nodes){
for(int i= 0;i非递归深度优先遍历:后序遍历
void PostDFS(int root,Node* nodes){
stack s;
s.push(root);
int prev= -1;
while(!s.empty()){
int now = s.top();
if(nodes[now].children.size() != 0 // 还有子节点
&& prev != nodes[now].children.back()){ // 回溯,上一个节点是最后一个遍历的子节点
for(int i= nodes[now].children.size()-1; i>=0;--i){
int post = nodes[now].children[i];
s.push(post);
}
} else {
s.pop();
printf("%c ",nodes[now].data);// 出栈访问
}
prev = now;
}
}
1.2 广度优先遍历(Breath First Search)
广度优先遍历:从根节点开始从上到下按照层依次遍历。
上图树的广度优先遍历结果:
A → B → C → D → E → F → G → H → I → J
void BFS(int root,Node* nodes){
queue s;
s.push(root);
printf("%c ",nodes[root].data);// 入队访问
while(!s.empty()){
int now = s.front();
s.pop();
for(int i= 0;i 完整测试程序
#include
using namespace std;
struct Node{// 孩子表示法
char data;
vector children;
};
// 非递归深度优先遍历:先序遍历
void PreDFS(int root,Node* nodes){
stack s;
s.push(root);
while(!s.empty()){
int now = s.top();
s.pop();
printf("%c ",nodes[now].data);// 出栈访问
for(int i= nodes[now].children.size()-1; i>=0;--i){// 逆序遍历
int post = nodes[now].children[i];
s.push(post);
}
}
}
// 递归深度优先遍历:先序遍历
void RecurtionPreDFS(int root,Node* nodes){
printf("%c ",nodes[root].data);
for(int i= 0;i s;
s.push(root);
int prev= -1;
while(!s.empty()){
int now = s.top();
if(nodes[now].children.size() != 0 // 还有子节点
&& prev != nodes[now].children.back()){ // 回溯,上一个节点是最后一个遍历的子节点
for(int i= nodes[now].children.size()-1; i>=0;--i){
int post = nodes[now].children[i];
s.push(post);
}
} else {
s.pop();
printf("%c ",nodes[now].data);// 出栈访问
}
prev = now;
}
}
// 递归深度优先遍历:后序遍历
void RecurtionPostDFS(int root,Node* nodes){
for(int i= 0;i s;
s.push(root);
printf("%c ",nodes[root].data);// 入队访问
while(!s.empty()){
int now = s.front();
s.pop();
for(int i= 0;i 练习
- LeetCode 589. N叉树的前序遍历
- LeetCode 590. N叉树的后序遍历
- LeetCode 429. N叉树的层序遍历
- LeetCode 559. N叉树的最大深度
枪挑一条线、棍扫一大片
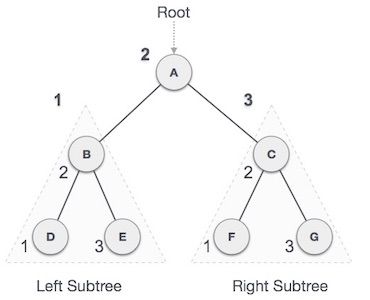
2. 二叉树遍历
二叉树通常使用链式存储。
struct Node{// 孩子表示法
char data;
struct Node* right;
struct Node* left;
};
二叉树的广度优先遍历与多叉树的广度优先遍历是一样的,因为是层次遍历,所以也称为层次遍历。
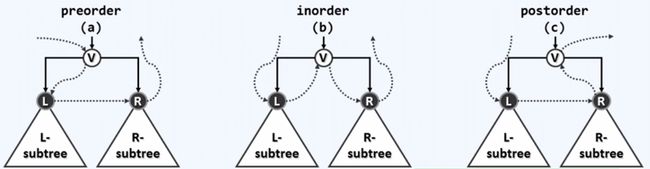
二叉树的深度优先遍历,根据父节点与左右子节点访问顺序的不同,而分为三类:
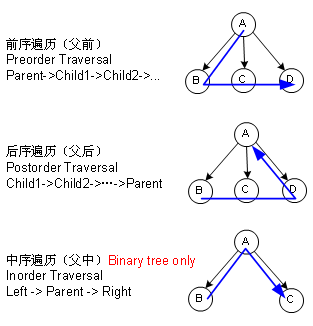
- 前序遍历(Pre-order Traversal)
- 中序遍历(In-order Traversal)
- 后序遍历(Post-order Traversal)
深度优先遍历三种遍历方式各有两种实现方式。
2.1 深度优先遍历
2.1.1 前序遍历(Pre-order Traversal)
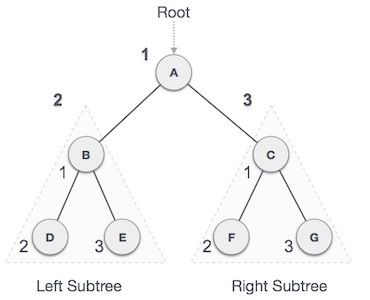
上图前序遍历结果:
A → B → D → E → C → F → G
前序遍历步骤:
- 访问根节点
- 递归遍历左子树
- 递归遍历右子树
直到所有节点都被访问。
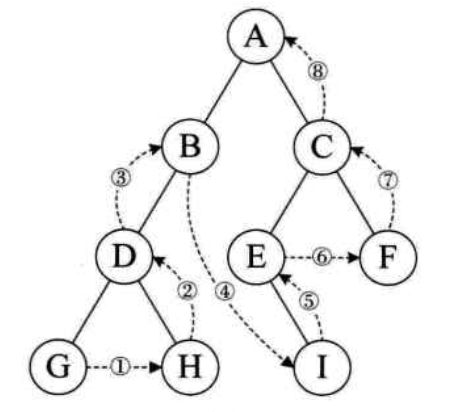
2.1.2 后序遍历(Post-order Traversal)
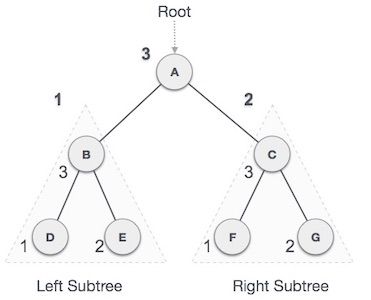
上图后序遍历结果:
D → E → B → F → G → C → A
后序遍历步骤:
- 访问根节点
- 递归遍历右子树
- 递归遍历左子树
直到所有节点都被访问。
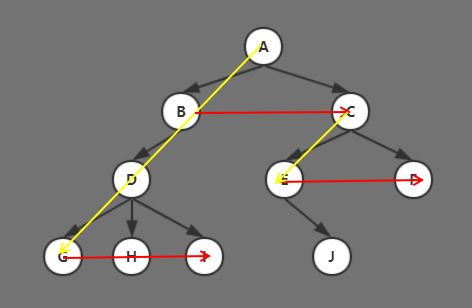
2.1.3 中序遍历(In-order Traversal)
上图中序遍历结果:
D → B → E → A → F → C → G
中序遍历步骤:
- 递归遍历左子树
- 访问根节点
- 递归遍历右子树
直到所有节点都被访问。
2.2 广度优先遍历
上图后序遍历结果:
A → B → C → D → E → F → G
后序遍历步骤:
- 访问根节点
- 按层次从上到下依次遍历
完整测试程序
#include
using namespace std;
struct Node{// 孩子表示法
char data;
struct Node* left;
struct Node* right;
};
// 递归深度优先遍历:先序遍历
void RecurtionPreDFS(Node* nodes){
if(NULL != nodes){
printf("%c ",nodes->data);
RecurtionPreDFS(nodes->left);
RecurtionPreDFS(nodes->right);
}
}
// 递归深度优先遍历:后序遍历
void RecurtionPostDFS(Node* nodes){
if(NULL != nodes){
RecurtionPostDFS(nodes->left);
RecurtionPostDFS(nodes->right);
printf("%c ",nodes->data);
}
}
// 递归深度优先遍历:中序遍历
void RecurtionInDFS(Node* nodes){
if(NULL != nodes){
RecurtionInDFS(nodes->left);
printf("%c ",nodes->data);
RecurtionInDFS(nodes->right);
}
}
// 非递归深度优先遍历:先序遍历
void PreDFS2(Node* nodes){
if(NULL == nodes) return;
stack s;// 保存已访问的节点
s.push(nodes);
while(!s.empty()){
Node* now = s.top();
s.pop();
printf("%c ",now->data);
if(NULL != now->right) s.push(now->right);
if(NULL != now->left) s.push(now->left);
}
}
void PreDFS(Node* nodes){
stack s;
Node* now = nodes;
while(NULL != now||!s.empty()){
if(NULL != now){
printf("%c ",now->data); // 打印节点
s.push(now);
now = now->left; // 左侧有节点
}else{
Node* p = s.top();
s.pop();
now = p->right;
}
}
}
// 非递归深度优先遍历:中序遍历
void InDFS2(Node* nodes){
stack s;
Node* now = nodes;
while(NULL != now||!s.empty()){
if(NULL != now){
s.push(now);
now = now->left; // 左侧有节点
}else{
Node* p = s.top();
s.pop();
printf("%c ",p->data); // 打印节点
now = p->right;
}
}
}
// 中序
void InDFS(Node* nodes){
stack s;
Node *prev = NULL,*now = NULL; // 记录当前节点和上一个节点之间的关系
s.push(nodes);
while(!s.empty()){
now = s.top();
if(NULL == prev // now为根节点
|| prev->left == now || prev->right == now // prev是now的父节点
){
if(NULL != now->left){
s.push(now->left); // 左孩子入栈
}else if(NULL != now->right){
s.push(now->right); // 右孩子入栈
}
}else if(now->left == prev){ // prev是now的左孩子(回溯)
printf("%c ",now->data); // 打印节点
if(NULL != now->right){
s.push(now->right); // 右孩子入栈
}
}else if(now->right == prev){ // prev是now的右孩子(回溯)
s.pop();
}else{
printf("%c ",now->data); // 打印节点
s.pop();
}
prev = now;
}
}
// 非递归深度优先遍历:后序遍历
// 使用双栈,将先序遍历逆序
void PostDFS(Node* nodes){
stack s;
stack t; //1.添加结果栈
Node* now = nodes;
while(NULL != now||!s.empty()){
if(NULL != now){
t.push(now); // 2.将打印数据入栈
s.push(now);
now = now->right; // 3.左右调换
}else{
Node* p = s.top();
s.pop();
now = p->left; // 3.左右调换
}
}
while(!t.empty()){ // 4.打印结果栈
Node* p = t.top();
t.pop();
printf("%c ",p->data); // 打印节点
}
}
void PostDFS2(Node* nodes){
stack s;
Node *prev = NULL,*now = NULL; // 记录当前节点和上一个节点之间的关系
s.push(nodes);
while(!s.empty()){
now = s.top();
if(NULL == prev // now为根节点
|| prev->left == now || prev->right == now // prev是now的父节点
){
if(NULL != now->left){
s.push(now->left); // 左孩子入栈
}else if(NULL != now->right){
s.push(now->right); // 右孩子入栈
}
}else if(now->left == prev){ // prev是now的左孩子(回溯)
if(NULL != now->right){
s.push(now->right); // 右孩子入栈
}
}else{
printf("%c ",now->data); // 打印节点
s.pop();
}
prev = now;
}
}
// 广度优先遍历
void BFS(Node* nodes){
queue s;
s.push(nodes);
printf("%c ",nodes->data);// 入队访问
while(!s.empty()){
Node* now = s.front();
s.pop();
if(NULL != now->left){
s.push(now->left);
printf("%c ",now->left->data);// 入队访问
}
if(NULL != now->right){
s.push(now->right);
printf("%c ",now->right->data);// 入队访问
}
}
}
int Depth(Node* nodes){
if(NULL == nodes) return 0;
return max(Depth(nodes->right),Depth(nodes->right))+1;
}
// 递归广度优先遍历
void RecurtionBFS(Node* nodes,int level){
if(NULL == nodes || 0 == level) return;
if(1 == level){
printf("%c ",nodes->data);
}
RecurtionBFS(nodes->left,level-1);
RecurtionBFS(nodes->right,level-1);
}
void RecurtionBFS(Node* nodes){
if(NULL == nodes) return;
int dep = Depth(nodes);
for(int i=1;i<=dep;++i){
RecurtionBFS(nodes,i);
}
}
int main() {
// 叶子节点
Node d = {'D',NULL,NULL};
Node e = {'E',NULL,NULL};
Node f = {'F',NULL,NULL};
Node g = {'G',NULL,NULL};
// 分支节点
Node b = {'B',&d,&e};
Node c = {'C',&f,&g};
// 根节点
Node a = {'A',&b,&c};
Node* root = &a;
printf("\n递归深度优先遍历:先序遍历\n");
RecurtionPreDFS(root);
printf("\n递归深度优先遍历:后序遍历\n");
RecurtionPostDFS(root);
printf("\n递归深度优先遍历:中序遍历\n");
RecurtionInDFS(root);
printf("\n非递归深度优先遍历:先序遍历\n");
PreDFS(root);
printf("\n");
PreDFS2(root);
printf("\n非递归深度优先遍历:后序遍历\n");
PostDFS(root);
printf("\n");
PostDFS2(root);
printf("\n非递归深度优先遍历:中序遍历\n");
InDFS(root);
printf("\n");
InDFS2(root);
printf("\n广度优先遍历\n");
BFS(root);
printf("\n递归广度优先遍历\n");
RecurtionBFS(root);
printf("\n");
printf("树的深度:%d\n",Depth(root));
}
3.练习
练习
- LeetCode 100. 相同的树
- LeetCode 144. 二叉树的前序遍历
- LeetCode 94. 二叉树的中序遍历
- LeetCode 145. 二叉树的后序遍历
- LeetCode 102. 二叉树的层次遍历
- LeetCode 104. 二叉树的最大深度
- LeetCode 111. 二叉树的最小深度