week2，有监督学习（的线性机器学习模型）

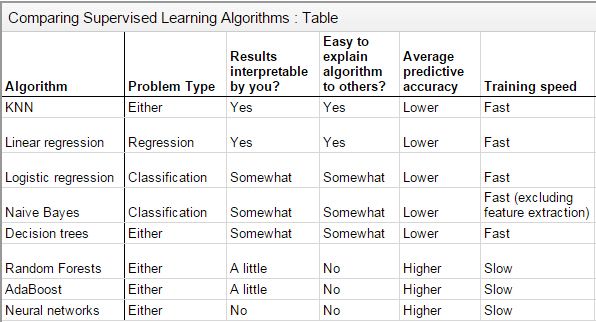
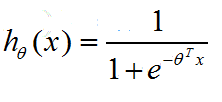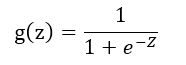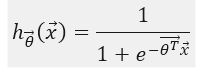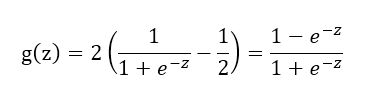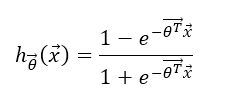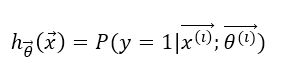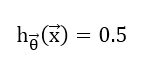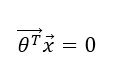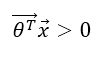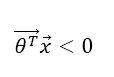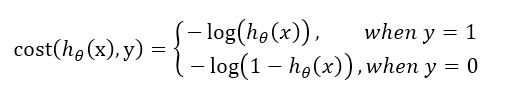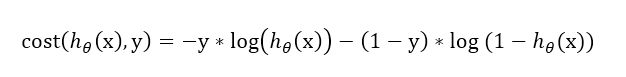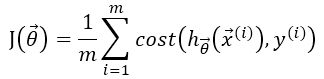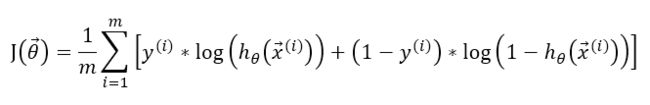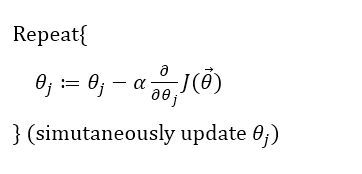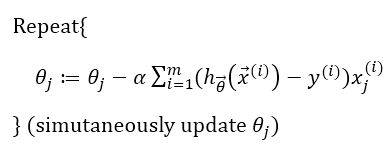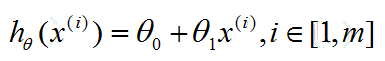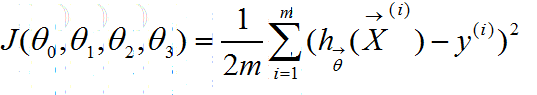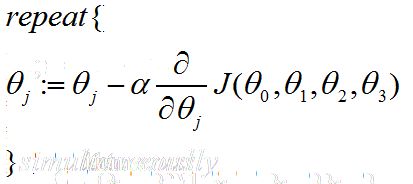2.1 有监督学习的描述：

有监督学习 是比较经典的一个机器学习场景。有监督学习可以被这样描述:

(1)Supervised learning is the machine learning task of inferring a function from labeled training data.[1] -监督学习完成“从labeled training data中推断出函数”的任务。
(2)labeled training data是由一对(input object, expected output)组成的数据。
(3)从labeled training data中学习到的函数可以将unseen instance的输入映射到输出(举个例子: 对于inferred function来说，我们再给它一个 input object 它就能够输出一个新的 expected output)。这种暗含在函数中的映射逻辑被称作inductive bias。(最简单的inductive bias就是occam's razor - Occam's razor, assuming that the simplest consistent hypothesis about the target function is actually the best. Here consistent means that the hypothesis of the learner yields correct outputs for all of the examples that have been given to the algorithm.)

最常用到的inductive bias：
Maximum conditional independence: if the hypothesis can be cast in a Bayesian framework, try to maximize conditional independence. This is the bias used in the Naive Bayes classifier.
Minimum cross-validation error: when trying to choose among hypotheses, select the hypothesis with the lowest cross-validation error. Although cross-validation may seem to be free of bias, the "no free lunch" theorems show that cross-validation must be biased.
Maximum margin: when drawing a boundary between two classes, attempt to maximize the width of the boundary. This is the bias used in support vector machines. The assumption is that distinct classes tend to be separated by wide boundaries.
Minimum description length: when forming a hypothesis, attempt to minimize the length of the description of the hypothesis. The assumption is that simpler hypotheses are more likely to be true. See Occam's razor.
Minimum features: unless there is good evidence that a feature is useful, it should be deleted. This is the assumption behind feature selection algorithms.
Nearest neighbors: assume that most of the cases in a small neighborhood in feature space belong to the same class. Given a case for which the class is unknown, guess that it belongs to the same class as the majority in its immediate neighborhood. This is the bias used in the k-nearest neighbors algorithm. The assumption is that cases that are near each other tend to belong to the same class.

2.2 有监督学习（supervised learning）的主要步骤：

(1)任务导向部分：
确定监督学习任务

• 分类(二分类，多分类)，多分类比二分类复杂在哪里？
• 回归(预测问题)

确定训练集的数据类型(图像，数字，音频？)

(2)数据工程部分:
收集训练集，数据预处理

(3)特征工程部分:
从数据集中选择有可能有用的特征，特征预处理， curse of dimensionality;

(4)模型工程部分:
根据任务特点选择有监督学习算法(不同的监督学习算法定义了不同的函数式，这里又叫hypothesis) ，如何合理地选择模型，衡量不同模型的优缺点参考：No free lunch theorem

(5)模型训练工程:
训练模型，计算cost function,计算optimization function，可视化训练结果，把握好underfitting和overfitting，调整模型参数，继续训练模型

(6)模型评估工程：
评估模型，交叉验证，模型泛化能力 cross-validation.

这些步骤里面， “训练，计算cost function，使用optimization function” 这三步是需要迭代多次才能得到优秀结果的。
此外

• 在有监督学习下面 使用的 cost function 和 optimization function的种类有很多.。
• 而且对于同一种cost function 或 optimization function 在不同的有监督学习算法下面也有些许的不同之处，主要还是因为模型不一样，然后cost function 和 optimization function 对于不同模型 也改变了格式。(主要是要掌握每种cost function和optimization function的核心思想)

2.2.1 任务导向

2.1.1 分类任务

(1) 分类任务有两种:

分类任务有两种，其一是二分类任务，其二是多分类任务。
通常在实际应用中，都是多分类任务。

2.2.2 数据工程

2.2.3 特征工程

2.2.4 模型工程部分

2.2.4.1 分类模型

(1) 分类模型有两种:

分类任务有两种，其一是二分类任务，其二是多分类任务。
有监督学习里面可以的分类器，有适合做二分类的分类器(logistic regression, basic SVM)和天生就适合做多分类的分类器(K近邻，神经网络，朴素贝叶斯，决策树，拓展SVM)。

• 分类常用模型
• Linear classifiers
• Logistic regression
• Naive Bayes classifier
• Support vector machines
  • SVM with no kernel(又可以称作: SVM with linear kernel) 也是线性分类器
  • SVM with Gaussian kernel 作为非线性分类器
• k-nearest neighbor
• Decision trees
  • Random forests
• Neural networks

2.2.4.2使用分类模型执行分类任务

(1) 执行二分类任务:

二分类任务是最直接的分类任务，同时也是多分类任务的基础。
二分类任务主要步骤:

• 选择分类模型(如:logistic regression, support vector mahine)
• 设定类别(比如：我们有第0类和第1类)
• 设定二分类输出阈值(比如：设定logistic function的阈值为0.5)
• 设定二分类规则(比如:输出小于阈值则分为第0类，输出大于阈值则分为第1类)。

举个例子:
<1> 选择分类模型:
假设使用logistic regression作二分类问题
logistic regression的hypothesis(即模型的函数表达式)是：

(theta 和 x都是 N维向量，N代表输入特征个数)

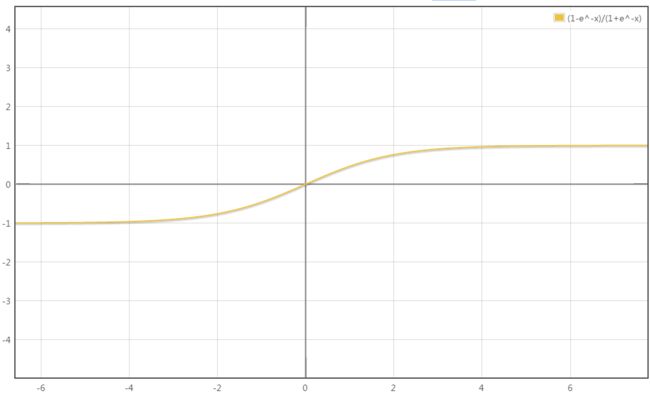
其hypothesis的函数图像是:

(纵轴是h_theta(x),横轴是 -theta*x)

<2> 设定有第0类和第1类:

<3> 我们设定阈值为: h_theta(x)=0.5。 分类规则为：小于0.5算作第0类， 大于0.5算作第1类。则此时可知：

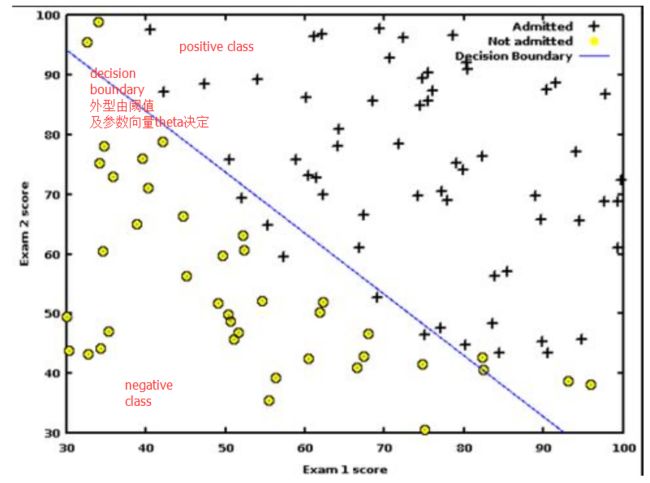
• 一次函数thetaX=0是当前二分类问题的decision boundary。该函数图像的特征由具体从训练中学习到的theta参数值决定。
• 当thetaX < 0时: 当前训练样本X(i)被分作第0类

• 当thetaX > 0时: 当前训练样本X(i)被分作第1类。
  此时我们可以画出关于theta*X=0的函数，并称该函数为decision boundary，可以发现，decision boundary将其左右两边分作了不同类，完成了分类任务，至于分类效果，就涉及了如何调参等问题。(以theta, X二维为例)：

  
  
  

  二分类decision boundary图像

(2) 执行多分类任务

多分类任务的重点在于‘进行多分类的手段’，常见应用于解决多分类问题的方法有三种：

The existing multi-class classification techniques can be categorized into (i) Transformation to binary (ii) Extension from binary and (iii) Hierarchical classification.[1] -三种解决多分类问题的方法：
1.将多分类问题拆分成多个二分类问题(常见的手段有：one-vs-all/又叫one-vs-rest, 和 one-vs-one又叫all-vs-all)
2.将二分类技术拓展成多分类技术(如:拓展SVM，神经网络)
3.进行层次分类

<1> 将多分类问题拆成多个二分类问题:

one-vs-all(one-vs-rest)

one-vs-all的主要思想就是:

• 对于一个N分类问题，为N个类别都构建一个二分类器(所以one-vs-all一共产生N个分类器)，使得每个分类器将当前类别分作一类、其余类别统一算作另一类。
• 对一个new instance进行分类时，需要将该instance带入N个分类器中进行计算，然后选取分类器输出最大的那个类作为分类结果。(值得注意的是:进行one-vs-all分类时，分类器必须输出real-valued confidence score而不仅仅是class label，因为，对于一个new instance来说，N个分类器的分类结果多多少少会有不精确、重叠的地方，假设让one-vs-all中的分类器都以Label的形式进行输出的话，最后可能同一个instance会有几个分类器都输出1，此时就不好判断new instance到底属于哪个类别)

one-vs-one(all-vs-all)

one-vs-one的主要思想就是:

• 对于一个N分类问题，我们需要以排列组合的方式，为N个类中每2个类构造一个分类器，one-vs-one的分类器输出的是class label,并不需要real-valued confidence score(所以one-vs-one分类器一共产生N(n-1)/2个分类器)。
• 对一个new instance进行分类时，需要将该instance带入N(N-1)/2个分类器中分别计算。显然，N(N-1)/2个分类器会针对该new instance到底属于N个类中的哪个类别进行投票，我们选择票数最高的类别作为当前instance的类型。

<2> 二分类模型拓展成多分类模型:
以下分类器可以直接进行多分类：

• Neural networks
• Extreme learning machines
• k-nearest neighbours
• Naive Bayes
• Decision trees
• Support vector machines

<3> 进行层次分类:

Hierarchical classification tackles the multi-class classification problem by dividing the output space i.e. into a tree. Each parent node is divided into multiple child nodes and the process is continued until each child node represents only one class. Several methods have been proposed based on hierarchical classification.
--层次分类法首先将所有类别分成两个子类，再将子类进一步划分成两个次级子类，如此循环，直到得到一个单独的类别为止。对层次支持向量机的详细说明可以参考论文《支持向量机在多类分类问题中的推广》

2.2.4.3 分类模型详解

(1) Logistic Regression（逻辑回归）
Logistic Regression是由一种基于概率解释的线性分类模型，可以解决：
<1> 二分类问题(使用sigmoid function将函数值映射到(0,1)概率区间内)
<2> 多分类问题(需要用到one-vs-all或者one-vs-one)。
Logistic Regression的模型(hypothesis)可以说是用 sigmoid function套上Linear Regression的hypothesis得来的。

• Logistic Regression的hypothesis:

• 假设Linear Regression的hypothesis为：

  
  
  

  theta和x为N维向量，代表训练样本有N维特征

• Sigmoid Function(又叫Logistic Function)为:

  
  
  

• 将Linear Regression的hypothesis作为z带入Sigmoid Function中即得到Logistic Regression的hypothesis:
  

  
  
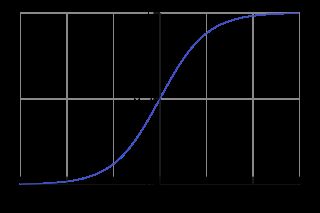
  其hypothesis的函数图像是:
  
  

  (纵轴是h_theta(x),横轴是 theta*x)
  
  ps: Logistic Regression的sigmoid function值域不是固定的而是可变化的,这样Logistic Regression的hypothesis的值域也是可以调整的，调整过函数外型的hypothesis，可以让Logistic Regression的分类功能更定制化，比如：用1表示positive class 而用 -1表示negative class(而且这里值得注意的是，当hypothesis改变时，cost function的表达式同样也要重新推理过，optimization function表达式也要重新推理过)。
  举个例子：
  <1>使用这样一个sigmoid function作为Logistic Regression hypothesis的外框架：该sigmoid function以[-1,1]为值域，使用-1表示negative class,使用1表示positive class。
  
  
  
  
  
  
  <2>此时Logistic Regression的hypothesis表达式则变化成:
  
  
  
  <3>此时cost function应该是:(这里是暂时猜测，还没验证对不对)
  
  

• Logistic Regression基于概率解释二分类问题
  对于一个训练样本的特征向量X(i), Logistic Regression hypothesis current的参数向量是theta(i)，那么hypothesis的计算结果可以表示为：
  

  
  
  hthetax的值就是使用当前模型Logistic Regression和参数theta估计的，样本i属于y=1(第一类)类的概率值P。

• Logistic Regression hypothesis的阈值与分类，Decision Boundary
  <1>阈值与分类
  二分类问题对训练样本进行分类的决策逻辑在于‘怎样判别样本i是属于1类(positive class)还是0类(negative class)’。Logistic Regression是基于概率解释的分类模型，显然地，可以通过设定阈值p，当样本i关于hypothesis的结果值（概率值）大于p时，我们说样本i被分作1类。当结果值小于p时，我们说样本i被分作0类。
  <2>阈值与Decision Boundary
  前面说过，Logistic Regression hypothesis的阈值大小决定了二分类时的决策逻辑，也就是说通过确定样本i的hypothesis结果值确定了样本i该属于哪一类。同样的，阈值和当前训练参数的值共通以Decision Boundary的形式，将分类结果体现在了图像上面。
  举个例子：
  使用Logistic Regression进行二分类问题，定义阈值为:
  

  

  阈值
  
  当htheta大于0.5时，样本i属于第1类(positive class), 当htheta小于0.5时，样本i属于第0类(negative class)。
  我们已知Logistic Regression hypothesis的函数图像是:
  
  

  (纵轴是h_theta(x),横轴是 theta*x)
  
  因此，我们可以知道关于函数thetaX的阈值是:
  
  
  
  对于训练样本i，如果:
  
  
  
  则训练样本i的ththeta大于0.5，训练样本i为第1类(positive class)。
  而如果:
  
  
  
  则训练样本i的ththeta小于0.5，训练样本i为第0类(negative class)。
  此外，因为当前训练好的参数值theta是已知的，所以我们可以直接将关于thetaX=0的函数画出来:
  
  
  
  那么显然，在thetaX=0函数右侧的都是带入thetaX大于0的训练样本i,因此会被分为positive class。在thetaX=0函数左侧的都是带入thetaX小于0的训练样本i,因此会被分为negative class。
  综上，Decision Boundary是由hypothesis的阈值以及当前训练好的关于hypothesis的参数共通决定。同时，Decision Boundary也从函数图像一侧体现了当前Logistic Regression的配置下(阈值和参数已定)的分类结果。

• Logistic Regression的cost function
  cost function作为机器学习算法中的optimization objective(优化函数进行优化的目标)是必须有的，并且cost function的优劣直接影响了机器学习的结果。
  对于Logistic Regression来说，通常使用-log表达它的cost function。对于单个训练样本，有cost function方程组：
  

  
  
  根据数学上的技巧，可以写出上述方程组的等价表达式：
  
  
  
  因此，假设训练集有m个训练样本，那么，Logistic Regression的cost function可以表示为：
  
  
  
  
  
  
  要理解为什么用log函数表达Logistic Regression的cost function，就要联系hypothesis的图像与log图像的关系：
  我们已知Logistic Regression hypothesis的函数图像是:
  
  

  (纵轴是h_theta(x),横轴是 theta*x)
  
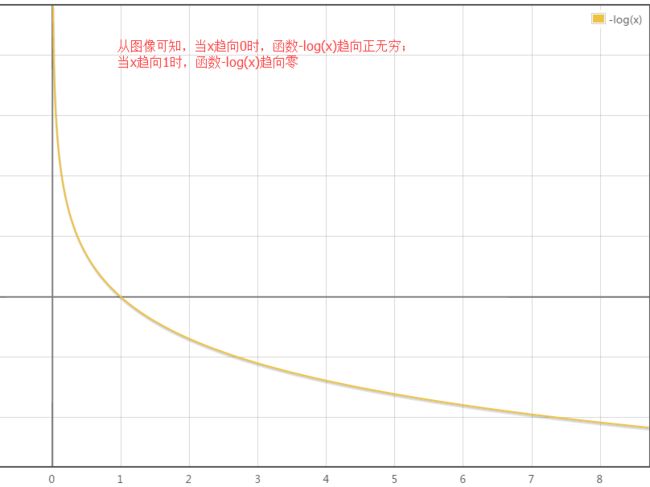
  -log(x)函数的图像是:
  
  
  
  因此:
  <1>当excepted output: y = 1时，hypothesis函数值越接近1，Logistic Regression 的 cost function值越小；hypothesis函数值越接近0，Logistic Regression的cost function值接近无穷大。
  <2>当excepted output: y = 0时，hypothesis函数值越接近0，则1-hypothesis的值越接近1，此时Logistic Regression的cost function值越小；hypothesis函数值越接近1, 则1-hypothesis的值越接近0，此时Logistic Regression的cost function值接近无穷。
  这样一来，cost function的值正好表示了当前Logistic Regression分类效果的好与坏。

• Logistic Regression的optimization function
  优化Logistic Regression的cost function,可以使用经典的Gradient descent方法。
  对于cost function:
  

  
  
  我们想要：
  
  
  
  则要：
  
  

  alpha是learning rate
  
  偏导解出来是:
  
  

• 关于Logistic Regression的优化函数：

• Gradient Descent

• Conjugate Gradient

• BFGS

• L-BFGS
  conjugate gradient, BFGS和L-BFGS的优点都是不需要自己选取learning rate alpha

(2) Support Vector Machine（支持向量机）
支持向量机作为同时支持线性和非线性分类的分类模型，也支持二分类和多分类问题。SVM的算法模型

2.2.4.4 回归任务（经常用于预测） ！！！！这里涉及大量统计学，还需要学习后补全知识点

回归的定义：回归是一种估计自变量(independent variable)和因变量(dependent variable)之间的对应关系的统计学方法。- 以统计学的角度说，回归就是：regression analysis estimates the conditional expectation of the dependent variable given the independent variables。

• 回归函数：通过回归的方法得到的：“由自变量估计因变量的函数”就叫做Regression function。
• 概率散布：如果将Regression function和训练样本点画出来，那么训练样本的dependent variable值在Regression function周围的散布叫做probability distribution。
• 用于预测：由于回归的特性(估计函数自变量和因变量之间的变化关系)，所以回归主要被用来做预测任务。

2.2.5 模型训练工程

监督学习的cost function（还需完善）

In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. supervised learning tasks such as regression or classification can be formulated as the minimization of a loss function over a training set. Hence,The loss function quantifies the amount by which the prediction deviates from the actual values. --在统计学中，loss function被用在参数估计中。而监督学习的方法，从参数估计的角度来说可以被定义为：“监督学习就是那些通过不断修改自身模型(函数)的参数从而达到满意效果的regression 或者 classification任务”。 因此，监督学习天然地需要借用cost function作为参数估计的手段，使用cost function去估量：当前的监督学习模型的参数估计的结果和真实参数的差距。

常见的Loss function：
包括log对数损失函数，平方损失函数，指数损失函数，Hinge损失函数

常见的optimization function（还需完善）

我目前知道的包括 梯度下降， normal equation， conjugate gradient, BFGS, L-BFGS

常见的有监督学习算法:

hypothesis

hypothesis在这里被用在有监督学习的线性学习方法的函数表示上。
比如: linear regression 的 hypothesis 就可以是:

这是一个具有一维特征的linear regression hypothesis。
其中， theta代表hypothesis中的参数，x uppercase i代表第i个样本的输入特征值。

损失函数详解

• 目前所知道的，损失函数对于 有监督学习(包括回归，分类和深度学习)来说是重要的，而对于其他机器学习场景，暂时不清楚是不是需要用到损失函数（比如：无监督学习貌似是不需要用到损失函数的）。
• 损失函数的作用： 有监督学习通过计算“训练过程中得到的真实输出(the practical output)” 和 训练样本的标签值(期望输出值expected output) 之间的距离（差距），将得到的距离（差距）作为调整整个模型的参照。对于优化函数(optimization function)来说，损失函数计算的值就是它们的输入值，不管是哪种优化函数，其核心的优化思想就是：“根据损失值，合理地、更好地调整整个模型的表现P”。
• 损失函数是关于参数theta的函数，hypothesis是关于样本输入特征x的函数。

线性有监督机器学习后三步的细节

• 首先，确认有监督机器学习的hypothesis，比如,以m个具有三个特征的样本的训练集和linear
  regression算法为例：

我们后面为了cost function 和 optimization function方便，需要假设x0 = 1.
所以我们有:

• 然后，根据hypothesis，和需要使用哪种cost function类型以及将会结合的optimization function，确认当前cost function的式子。比如，我们这里使用squared error function作为cost function，后面使用gradient descent作为optimization function，则我们有:

其中，y uppercase i值得是对应于第i个输入训练样本的期望输出expected output。
这里设置1/2m而不是1/m的原因是我们后面会使用gradient descent作为optimization function,而gradient descent其中有求导数的步骤，那么指数2和分数1/2就会抵消掉，这样就简化了计算。

• 现在，我们确认optimization function的格式，由于我们用的是gradient descent，所以有：

注意，对于所有的theta 我们需要同时进行更新。

• 最后根据之前的cost function 和 optimization function，同时计算出了最新的theta参数。
  然后再次重复以上步骤，计算cost function 和 optimization function，更新theta参数，直到cost function 计算出的loss 小于我们预先设定的阈值

image.png