Floyd(弗洛伊德)算法(C语言)

转载：https://blog.csdn.net/qq_35644234/article/details/60875818

 

Floyd算法的介绍

算法的特点

弗洛伊德算法是解决任意两点间的最短路径的一种算法，可以正确处理有向图或有向图或负权（但不可存在负权回路)的最短路径问题，同时也被用于计算有向图的传递闭包。

算法的思路

通过Floyd计算图G=(V,E)中各个顶点的最短路径时，需要引入两个矩阵，矩阵S中的元素a[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。矩阵P中的元素b[i][j]，表示顶点i到顶点j经过了b[i][j]记录的值所表示的顶点。

假设图G中顶点个数为N，则需要对矩阵D和矩阵P进行N次更新。初始时，矩阵D中顶点a[i][j]的距离为顶点i到顶点j的权值；如果i和j不相邻，则a[i][j]=∞，矩阵P的值为顶点b[i][j]的j的值。 接下来开始，对矩阵D进行N次更新。第1次更新时，如果”a[i][j]的距离” > “a[i][0]+a[0][j]”(a[i][0]+a[0][j]表示”i与j之间经过第1个顶点的距离”)，则更新a[i][j]为”a[i][0]+a[0][j]”,更新b[i][j]=b[i][0]。 同理，第k次更新时，如果”a[i][j]的距离” > “a[i][k-1]+a[k-1][j]”，则更新a[i][j]为”a[i][k-1]+a[k-1][j]”,b[i][j]=b[i][k-1]。更新N次之后，操作完成！

 

补充：以下面图为例子，b[i][j]中存储的是Vi~Vj之间的中介点，b[i][j]初始值为j，比如V0~V3最短路径是V0-->V2-->V1-->v3，在计算最短路径时转换为V0-->V2的距离加上V2-->V3的最短距离，接下来类似于递归，V2-->V3的最短路径就是以V1为中介点，V2-->V1的距离加上V1-->V3的距离。因此，b[0][3]=2

 

实例说明

 

 

 

将整体分为两个步骤

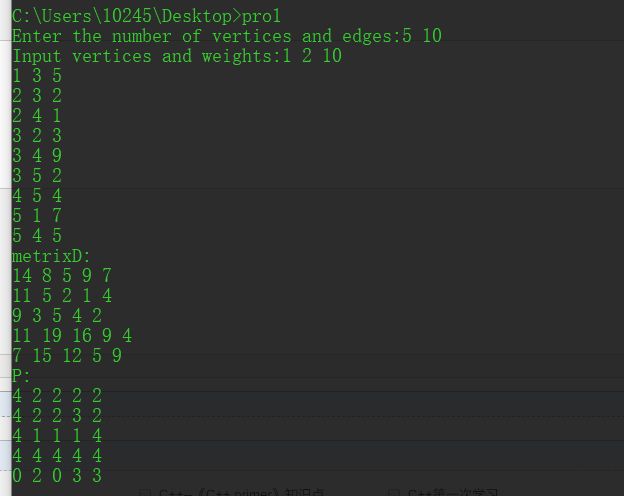
1.计算metrixD矩阵(两顶点之间的最短距离)和P矩阵(两顶点的中介点)

#include 
#include 

void Create_metrixD_P(int** metrixD, int **P ,int VerNum, int EdgNum)
{
    int x, y, Weight, edg_count = 0;
    int i, j, k;

    for (i = 0; i < VerNum; ++i) {
        for (j = 0; j < VerNum; ++j) {
            metrixD[i][j] = INT_MAX;
            P[i][j] = j;
        }
    }

    while (edg_count < EdgNum) {
        scanf("%d%d%d", &x, &y, &Weight);
        metrixD[x - 1][y - 1] = Weight;
        edg_count++;
    }
}

//Floyd algorithm
void Floyd(int **metirxD, int **P, int VerNum) {
    int n, x, y, temp = 0;
    //The triple loop looks for shortest paths and weights
    for (n = 0; n < VerNum; ++n) {
        for (x = 0; x < VerNum; ++x) {
            for (y = 0; y < VerNum; ++y) {
                //The distance between two vertices is compared to the distance through a vertex
                temp = (metirxD[x][n] == INT_MAX || metirxD[n][y] == INT_MAX) ? INT_MAX : (metirxD[x][n] + metirxD[n][y]);
                if (temp < metirxD[x][y]) {
                    //Update matrix information
                    metirxD[x][y] = temp;
                    P[x][y] = n;
                }
            }
        }
    }
}

void Show_metrixD_P(int** metrixD, int **P, int VerNum)
{
    int x, y;
    printf("metrixD:\n");
    for (x = 0; x < VerNum; ++x) {
        for (y = 0; y < VerNum; ++y) {
            if (metrixD[x][y] == INT_MAX) {
                printf("∞ ");
            }
            else {
                printf("%d ", metrixD[x][y]);
            }
        }
        printf("\n");
    }
    printf("P:\n");
    for (x = 0; x < VerNum; ++x) {
        for (y = 0; y < VerNum; ++y) {
            printf("%d ", P[x][y]);
        }
        printf("\n");
    }
}

int main(void)
{
    int VerNum, EdgNum, i;
    int** metrixD, ** P;

    printf("Enter the number of vertices and edges:");
    scanf("%d%d", &VerNum, &EdgNum);

    metrixD = (int**)malloc(VerNum * sizeof(int));
    P = (int**)malloc(VerNum * sizeof(int));

    for (i = 0; i < VerNum; ++i) {
        metrixD[i] = (int*)malloc(VerNum * sizeof(int));
        P[i] = (int*)malloc(VerNum * sizeof(int));
    }

    printf("Input vertices and weights:");
    Create_metrixD_P(metrixD, P, VerNum, EdgNum);
    Floyd(metrixD, P, VerNum);
    Show_metrixD_P(metrixD, P, VerNum);

    for (i = 0; i < VerNum; ++i) {
        free(metrixD[i]);
        free(P[i]);
    }
    free(metrixD);
    free(P);

    return 0;
}

 

2.输出顶点之间的最短距离与路径

#include 
#include 

#define VEXNUM 5

//Adjacency matrix: shows the distance between vertices
int metirxD[VEXNUM][VEXNUM] = {
INT_MAX,10,        5,        INT_MAX,INT_MAX,
INT_MAX,INT_MAX,2,        1,        INT_MAX,
INT_MAX,3,        INT_MAX,9,        2,
INT_MAX,INT_MAX,INT_MAX,INT_MAX,4,
7,        INT_MAX,INT_MAX,5,        INT_MAX
};

//Path: passing vertex between two vertices
int P[VEXNUM][VEXNUM] = {
0,1,2,3,4,
0,1,2,3,4,
0,1,2,3,4,
0,1,2,3,4,
0,1,2,3,4
};

//Floyd algorithm
void Floyd() {
    int n, x, y, temp = 0;
    //The triple loop looks for shortest paths and weights
    for (n = 0; n < VEXNUM; ++n) {
        for (x = 0; x < VEXNUM; ++x) {
            for (y = 0; y < VEXNUM; ++y) {
                //The distance between two vertices is compared to the distance through a vertex
                temp = (metirxD[x][n] == INT_MAX || metirxD[n][y] == INT_MAX) ? INT_MAX : (metirxD[x][n] + metirxD[n][y]);
                if (temp < metirxD[x][y]) {
                    //Update matrix information
                    metirxD[x][y] = temp;
                    P[x][y] = n;
                }
            }
        }
    }
}

void Show_Path() {
    int x, y, temp = 0;
    //Output the shortest path between two vertices
    for (x = 0; x < VEXNUM - 1; ++x) {
        for (y = x + 1; y < VEXNUM; ++y) {
            printf("V%d-->V%d  weight:%d  path:V%d", x, y, metirxD[x][y], x);
            temp = P[x][y];
            while (temp != y) {
                printf("-->V%d", temp);
                temp = P[temp][y];
            }
            printf("-->V%d", y);
            printf("\n");
        }
    }
}

int main(void)
{
    Floyd();
    Show_Path();

    return 0;
}

 

完整代码

#include 
#include 

void Create_metrixD_P(int** metrixD, int **P ,int VerNum, int EdgNum)
{
    int x, y, Weight, edg_count = 0;
    int i, j, k;

    for (i = 0; i < VerNum; ++i) {
        for (j = 0; j < VerNum; ++j) {
            metrixD[i][j] = INT_MAX;
            P[i][j] = j;
        }
    }

    while (edg_count < EdgNum) {
        scanf("%d%d%d", &x, &y, &Weight);
        metrixD[x - 1][y - 1] = Weight;
        edg_count++;
    }
}

//Floyd algorithm
void Floyd(int **metirxD, int **P, int VerNum) {
    int n, x, y, temp = 0;
    //The triple loop looks for shortest paths and weights
    for (n = 0; n < VerNum; ++n) {
        for (x = 0; x < VerNum; ++x) {
            for (y = 0; y < VerNum; ++y) {
                //The distance between two vertices is compared to the distance through a vertex
                temp = (metirxD[x][n] == INT_MAX || metirxD[n][y] == INT_MAX) ? INT_MAX : (metirxD[x][n] + metirxD[n][y]);
                if (temp < metirxD[x][y]) {
                    //Update matrix information
                    metirxD[x][y] = temp;
                    P[x][y] = n;
                }
            }
        }
    }
}

void Show_metrixD_P(int** metrixD, int **P, int VerNum)
{
    int x, y;
    printf("metrixD:\n");
    for (x = 0; x < VerNum; ++x) {
        for (y = 0; y < VerNum; ++y) {
            if (metrixD[x][y] == INT_MAX) {
                printf("∞ ");
            }
            else {
                printf("%d ", metrixD[x][y]);
            }
        }
        printf("\n");
    }
    printf("P:\n");
    for (x = 0; x < VerNum; ++x) {
        for (y = 0; y < VerNum; ++y) {
            printf("%d ", P[x][y]);
        }
        printf("\n");
    }
}

void Show_Path(int **metirxD, int **P, int VerNum) {
    int x, y, temp = 0;
    //Output the shortest path between two vertices
    for (x = 0; x < VerNum - 1; ++x) {
        for (y = x + 1; y < VerNum; ++y) {
            printf("V%d-->V%d  weight:%d  path:V%d", x, y, metirxD[x][y], x);
            temp = P[x][y];
            while (temp != y) {
                printf("-->V%d", temp);
                temp = P[temp][y];
            }
            printf("-->V%d", y);
            printf("\n");
        }
    }
}

int main(void)
{
    int VerNum, EdgNum, i;
    int** metrixD, ** P;

    printf("Enter the number of vertices and edges:");
    scanf("%d%d", &VerNum, &EdgNum);

    metrixD = (int**)malloc(VerNum * sizeof(int));
    P = (int**)malloc(VerNum * sizeof(int));

    for (i = 0; i < VerNum; ++i) {
        metrixD[i] = (int*)malloc(VerNum * sizeof(int));
        P[i] = (int*)malloc(VerNum * sizeof(int));
    }

    printf("Input vertices and weights:");
    Create_metrixD_P(metrixD, P, VerNum, EdgNum);
    Floyd(metrixD, P, VerNum);
    Show_metrixD_P(metrixD, P, VerNum);
    Show_Path(metrixD, P, VerNum);

    for (i = 0; i < VerNum; ++i) {
        free(metrixD[i]);
        free(P[i]);
    }
    free(metrixD);
    free(P);

    return 0;
}