题目描述
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2:
输入: "cbbd"
输出: "bb"
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/longest-palindromic-substring
题解
我的题解
我的思路(暴力法):查找所有的回文找出最长回文子串
我的做法:s的长度为0,不是回文,为1时,回文就是s本身,当s中的回文长度大于1时,回文的起始位置必定等于回文的结束位置,所以从s的起始位置开始依次查找是否存在相同的字符,如果存在,截取字符串判断是否为回文,是回文则判断是否为目前最长的回文,如果是目前最长的回文则记录,再依次查找下一个回文
public String longestPalindrome(String s) {
if (s.length() <= 1){
return s;
}
// 最大回文长度
int length = 0;
// 回文起始位置
int start = 0;
//回文结束位置(比实际大1,截取的时候包含头不包含尾)
int end = 0;
for (int i = 0; i length){
length=str.length();
start = i;
end = j+1;
}
}
}
}
return end>start?s.substring(start,end):s.substring(0,1);
}
/**
* 判断是否为回文
* @param s
* @return
*/
private static boolean huiwen(String s){
for (int i = 0; i 小插曲:代码写完了自测了一下通过了,那叫一个高兴啊,又解决一题,赶紧去提交代码,一提,不通过,啥?还有bug?,我再瞅瞅,嗯?超出时间限制了,有这么慢吗?再提一下,通过了,但是要1477ms,不过这种方法的确不好,时间复杂度为O(n^3),增长很快,来看一看官方题解是怎么做的吧!
官方题解
官方题解给了多种解题思路,其中暴力法也囊括其中(这大概是最容易想到的吧),下面只讲两种方法
1.动态规划法
public String longestPalindrome1(String s) {
int n = s.length();
String res = "";
boolean[] P = new boolean[n];
for (int i = n - 1; i >= 0; i--) {
for (int j = n - 1; j >= i; j--) {
P[j] = s.charAt(i) == s.charAt(j) && (j - i < 3 || P[j - 1]);
if (P[j] && j - i + 1 > res.length()) {
res = s.substring(i, j + 1);
}
}
}
return res;
}复杂度:
时间复杂度: O(n²)。
空间复杂度: O(n ) 。
官方并没有给代码,代码从精选题解中找出来的,并且进行了优化空间复杂度,不是很能看懂的建议自己去看,题目描述里面有链接
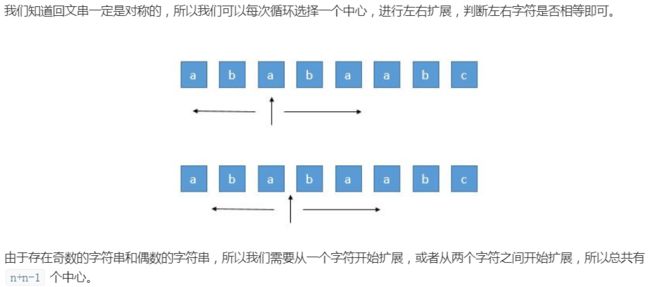
2.扩展中心法
public String longestPalindrome(String s) {
if (s == null || s.length() < 1) return "";
int start = 0, end = 0;
for (int i = 0; i < s.length(); i++) {
int len1 = expandAroundCenter(s, i, i);
int len2 = expandAroundCenter(s, i, i + 1);
int len = Math.max(len1, len2);
if (len > end - start) {
start = i - (len - 1) / 2;
end = i + len / 2;
}
}
return s.substring(start, end + 1);
}
private int expandAroundCenter(String s, int left, int right) {
int L = left, R = right;
while (L >= 0 && R < s.length() && s.charAt(L) == s.charAt(R)) {
L--;
R++;
}
return R - L - 1;
}复杂度:
时间复杂度:O(n²)
空间复杂度:O(1)