Problem
Description
Lavender、Caryophyllus、Jasmine、Dianthus现在在玩一款名叫“赛艇”的游戏。
这个游戏的规则是这样的:
- 玩家自由组成两队,一个人当赛艇的艇长,另一个人当侦察兵;
- 每次游戏开始时,双方均拥有由系统生成的某张地图,该地图以01矩阵的形式表示,
1表示有障碍物,无法通行,0表示水域空旷,可以通行; - 第一回合,双方的赛艇艇长都要在地图上指定一个出发点,该出发点不能是障碍物,也就是只能为
0; - 在每个回合中,艇长可以指挥自己的赛艇向上/下/左/右四个方向的某一方向的空旷水域移动一个单位的距离,也就是说只能移向四个方向上的某个
0上(当然,不能移动出地图之外);在该操作完成之后,必须向对方说出自己在该回合移动的方向; - 双方的侦察兵负责记录每一回合对方赛艇的移动方向,并负责推断此时对方赛艇可能的位置;如果某方的侦察兵推测出对方赛艇此时的精确位置,那么可以向其发射导弹,该侦察兵所在的一方胜利;
现在,Jasmine记录了一些对方赛艇的路径,她想确定一下此时对方所有可能的位置共有几种。由于她不是很擅长计算,所以这个任务就交给你了。
Input Format
输入第一行包含三个正整数 \(n\),\(m\),\(k\),分别表示地图为 \(n\) 行 \(m\) 列,当前游戏已经进行了 \(k\) 轮。
输入第二行到第 \(n+1\) 行为一个 \(n\) 行 \(m\) 列的 01 矩阵,无任何分隔符号,表示地图的具体信息,具体含义如上所示。
输入的最后一行为一个长度为 \(k\) 的字符串 \(s\),仅由字母 w、a、s、d 构成,从前往后第 \(i\) 个字符 \(s_i\) 表示对方在第 \(i\) 轮中,对方赛艇向上/左/下/右移动一个单位距离。
Output Format
输出一行一个正整数,表示在第 \(k\) 轮游戏回合的时候,对方赛艇可能的位置的种数。对于所有输入数据,保证有合法解。
Sample
Input
5 6 5
000000
001001
000100
001000
000001
dwdaaOutput
4Explanation
Explanation for Input
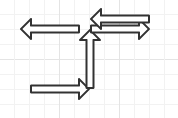
上图显示了路径序列可视化之后的结果,下图用蓝色标出了此时对方赛艇可能的位置。
Range
\(2\le n,m \le 1500, 1\le k\le 5\times 10^6\)
Algorithm
\(FFT\)
Mentality
套路题。
我们将走过的路径可视化,表示为一个矩阵。矩阵中为 \(1\) 的位置表示走到过,反之走不到。
那么这道题就相当于我们能够找到多少个点,满足将矩阵的左上角与这个点对齐后,矩阵中的 \(1\) 与原图中的 \(1\) 不重合。
考虑将矩阵的列数补齐至 \(m\) 列,然后将原图和矩阵分别拆成一维的数组 \(f,g\),即第一行后面接上第二行,第二行后面接上第三行这样的。
然后将矩阵拆出的 \(g\) 数组翻转得到 \(g'\),和 \(f\) 进行卷积得到 \(F\) 。
若 \(f\) 的长度为 \(a\),\(g\) 的长度为 \(b\),不难发现,对于一个满足要求的,原图中可以对齐矩阵左上角而合法的点 \((x,y)\) ,若其在 \(f\) 中对应第 \(i\) 个位置,矩阵的 \((0,0)\) 在 \(g\) 中对应 \(0\),在 \(g'\) 中对应 \(b-1\) ,那么以 \((x,y)\) 为左上角和矩阵相叠的结果将存在于 \(F\) 的第 \(i+b-1\) 中。
我们只需要对那些合法的,有足够空间去作为左上角叠下这个矩阵的点,统计它们在 \(F\) 中对应结果即可。
答案即为这些结果中 \(0\) 的个数。
Code
#include
#include
#include
using namespace std;
#define LL long long
#define go(x, i, v) for (int i = hd[x], v = to[i]; i; v = to[i = nx[i]])
#define inline __inline__ __attribute__((always_inline))
LL read() {
long long x = 0, w = 1;
char ch = getchar();
while (!isdigit(ch)) w = ch == '-' ? -1 : 1, ch = getchar();
while (isdigit(ch)) {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar();
}
return x * w;
}
const int Max_n = 1505, Max_l = 5e6 + 5, mod = 998244353, G = 3;
int n, m, K, ans, dx[5] = {0, -1, 1, 0, 0}, dy[5] = {0, 0, 0, -1, 1};
int lim, bit, rev[Max_l], f[Max_l], g[Max_l];
int s[Max_l], a[Max_n][Max_n];
char S[Max_l];
int ksm(int a, int b) {
int res = 1;
for (; b; b >>= 1, a = 1ll * a * a % mod)
if (b & 1) res = 1ll * res * a % mod;
return res;
}
namespace NTT {
void dft(int *f, bool t) {
for (int i = 0; i < lim; i++)
if (rev[i] > i) swap(f[i], f[rev[i]]);
for (int len = 1; len < lim; len <<= 1) {
int Wn = ksm(G, (mod - 1) / (len << 1));
if (!t) Wn = ksm(Wn, mod - 2);
for (int i = 0; i < lim; i += len << 1) {
int Wnk = 1;
for (int k = i; k < i + len; k++, Wnk = 1ll * Wnk * Wn % mod) {
int x = f[k], y = 1ll * Wnk * f[k + len] % mod;
f[k] = (x + y) % mod, f[k + len] = (x - y + mod) % mod;
}
}
}
}
} // namespace NTT
void ntt(int *f, int *g) {
NTT::dft(f, 0), NTT::dft(g, 0);
for (int i = 0; i < lim; i++) f[i] = 1ll * f[i] * g[i] % mod;
NTT::dft(f, 1);
int Inv = ksm(lim, mod - 2);
for (int i = 0; i < lim; i++) f[i] = 1ll * f[i] * Inv % mod;
}
int main() {
#ifndef ONLINE_JUDGE
freopen("5447.in", "r", stdin);
freopen("5447.out", "w", stdout);
#endif
n = read(), m = read(), K = read();
for (int i = 0; i < n; i++) {
scanf("%s", S);
for (int j = 0; j < m; j++) f[i * m + j] = S[j] == '1';
}
scanf("%s", S + 1);
for (int i = 1; i <= K; i++) {
if (S[i] == 'w') s[i] = 1;
if (S[i] == 's') s[i] = 2;
if (S[i] == 'a') s[i] = 3;
if (S[i] == 'd') s[i] = 4;
}
int sx = 0, sy = 0, l = 0, r = 0, u = 0, d = 0;
for (int i = 1; i <= K; i++) {
sx += dx[s[i]], sy += dy[s[i]];
l = min(l, sy), r = max(r, sy), u = min(u, sx), d = max(d, sx);
}
r -= l, sy = -l, l = 0, d -= u, sx = -u, u = 0;
a[sx][sy] = 1;
for (int i = 1; i <= K; i++) a[sx += dx[s[i]]][sy += dy[s[i]]] = 1;
for (int i = 0; i <= d; i++)
for (int j = 0; j < m; j++) g[i * m + j] = a[i][j] == 1;
for (int i = 0; i < (d + 1) * m / 2; i++) swap(g[i], g[(d + 1) * m - i - 1]);
bit = log2(n * m + (d + 1) * m) + 1, lim = 1 << bit;
for (int i = 0; i < lim; i++)
rev[i] = rev[i >> 1] >> 1 | ((i & 1) << (bit - 1));
ntt(f, g);
for (int i = 0; i < n - d; i++)
for (int j = 0; j < m - r; j++) ans += !f[(d + i + 1) * m + j - 1];
cout << ans;
}