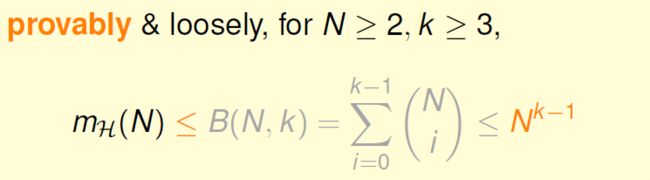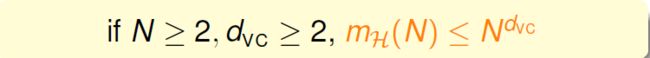Lec 7:The VC Dimension
tips:符号含义主要参照lec 1,部分需要参照其他lec
上一节介绍了机器学习可行性的重要理论保障VC Bound,基于此,这节将介绍VC Dimension.
1、Definition of VC Dimension
上一节讲到上限函数B(N,k)的最高次项是k的N - 1次方。
这里将B(N,k)与k的N-1次方做部分比较:
可以看出N的k-1次方已经比B(N,k)大了,实际上我们可以用N的k-1次方bound住B(N,k),可以简化bound:
所以bad data的概率上限现在可以更加简化,不过,要加上上面的条件N≥2 && k≥3:
小summary: H存在k并且N足够大时,可以保证Eout ≈ Ein,所以这时候当A选择一个Ein小的h作为g就probably learned(当然也是需要一点luck的)!
下面进入本节的重点,先给出VC Dimension 的定义。很简单,VC Dimension就是最大的那个非break-point。
稍正式点的定义:表示为dvc(H),为 largest N for which mH(N)= 2的N次方
vc dimension 是H的一个性质,还可以从下面两点看待,一是dvc就是H可以shatter的最大inputs数量;二是dvc = min(k) - 1.
结合上面的内容,成长函数的上限又可以表示为:
所以dvc有限就可以说H是good!有限的dvc就可以保障 Eout(g)≈ Ein(g).
2、Perceptrons Revisited
已知2D的Perceptrons的dvc=3,当N足够大时,learning可行!那当更一般化的、更高维的PLA会怎样呢?
回顾一下,1D的PLA的dvc = 2;2D的PLA的dvc = 3. 猜测:dvc = d + 1???恩,猜对了,哈哈哈,这里先给出结论再给出证明。
证明这个结论可以从两方面证明:一方面dvc ≥ d + 1;一方面 dvc ≤ d + 1
1)dvc ≥ d + 1
这一条代表什么?就是可以找出能够被shatter的d + 1 个inputs .
这里用一组特别的input,用矩阵表示,此矩阵存在反矩阵;y也用矩阵表示,y表示任意的二元组合。能够shatter就表示对于任意的y都能得到sign(Xw)= y .显然可以,所以成立。
2)dvc ≤ d + 1
这一条代表对于“任意”d+2维的inputs都不能shatter.
先看简单的例子 2D PLA. x4 可以被x1 x2 x3的线性组合表示,所以x1 x2 x3的正负确定后,x4的正负也就确定了!下图中x4 必然是正的。这里基本可以得出一个结论:线性依赖(linear dependence)关系限制了dichotomy的最大kind数量!
更一般的情况,X矩阵有d+2个rows、d+1个columns.row>col,所以会有线性依赖。前d+1个确定则d+2个自然就确定了,所以自然不能shatter!所以结论成立。
所以 dvc = d + 1.线性依赖限制了dichotomy的kind数量~
3、Degree of Freedom
dvc = d + 1,d是perceptron的维度,每个w对应一个h,w =(w0,w2,w3,...,wd),dvc代表的是有效的binary分类的自由度(就像调节按钮的调节范围)。自由度也代表了H的powerfulness(就是H能够做多少事情)。
在实际中,通常dvc ≈ 可以调节的参数的个数(but not always)
回想一下关于M的trade off,现在同样dvc有一样的问题(这是自然的,因为我们千辛万苦用N的dvc次方取代了M):
所以,使用合适大小的dvc是很重要的。
这一节的fun time有点意思,这里提一下:
答案是2.这里林老师的目的并不是让我们去证明,而是这样理解:w0已经固定,则可以调节的自由度就少了1个,则dvc是d +1-1.
4、进一步了解dvc的意义
回顾一下vc bound
vc bound限制了发生bad data 的概率,则good 的概率是 1 - δ。good即|Ein(g)- Eout(g)|≤ ε.经过下面的计算可以得到ε的表达式。
见下图,所以,Eout和Ein的差异的大小与dvc是有关的。gen是generalization的缩写。我们通常只需要关注右侧的bound就好了,左侧灰色在此可忽略。dvc大自由度高,但是需要付出更大的代价 ε. 右侧用Ω(N,H,δ) 表示,称为model complexity( 模型复杂度),这里的model可以理解为H.
根据上图中Eout和Ein的关系,我们要给出一个非常非常重要的图!!!
dvc ↑:Ein ↓(有更多机会找到好的g);但是Ω ↑ ;
dvc ↓:Ω ↓ ,但是 Ein ↑
通常最好的dvc在中间位置。
从这张图可以看出H并不是越powerful越好的!(太powerful就会overfiting,后面章节介绍)
之前我们只是想着把Ein变小,其实我们还要考虑需要付出的代价!
一直说需要足够多的data,那N是多少合适呢?根据vc bound 式子以及需求大致可以计算出需要的N的大小。理论上,我们需要 N = 10000 * dvc,太多了太难找到这么多data了。实际中 10 * dvc的data often enough !
why?
因为vc bound 很宽松(looseness),宽松的来源是什么?四点:
1)霍夫丁对任意分布的data以及f都适用;
2)mH(N)成长函数是采样出的any data 对应的dichotomy的最大值;
3)用N的dvc次方是成长函数的上限的上限的上限,我们只用一个值dvc去计算上限,可以忽略H的细节;
4)union bound是考虑了最坏的情况;
其实一路推导都很宽松,所以理论和实际差了很多。
讲了这么多,其实最重要的并不是它的理论部分,而是明白vc bound里面的“哲学”(都在最后一张图里了)。