序言
对于IT行业者来说,刚参加工作,还能找点借口,说自己不擅长算法。可是工作三年以上的IT开发者,还说自己不会算法,不会设计模式就说不过去了。所以最近开始撸算法和设计模式,重新开一个集记录算法的学习之路。算法在用户量比较少,或者计算量比较小的时候,影响确实不大,但是到达一定数量级的时候,算法的优劣就会极大的影响程序的顺畅程度。优秀的算法甚至能给人amazing的感觉。
今天记录《数据结构与算法分析——C语言描述》中的一个求最大子序列的问题。
问题
给定整书A1,A2,……,AN(可能有负数),设整数k取值i到j(i<=j),求Ai到Aj的和的最大值(所有整数均为负数,则最大子序列和为0)。
例:
输入-2,11,-4,13,-5,-2时,答案为20(从A2到A4)。
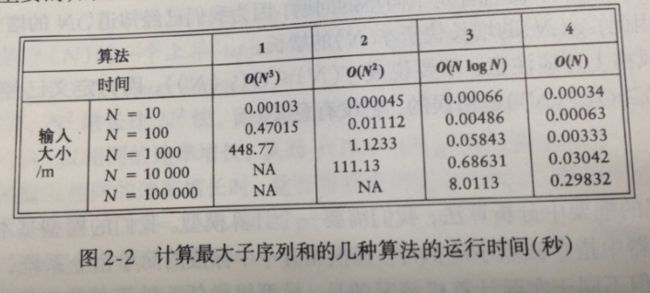
这个问题比较有代表性,原因是因为求解该问题有多种算法,但是这些算法的性能又差异非常大。后面将记录求解该问题的四种算法。这四种算法在书上的运行时间如下:
当然随着计算机设备的更新换代,现在的计算机运行速度肯定没这么慢。后面会给出实际的运行时间,还是先分析和记录算法吧。
算法1
算法1是穷举式的尝试所有的可能,用三重嵌套for循环来求解最大子序列,但是运行的时间非常慢,时间复杂度是O(N*N*N),即N的立方。
- (int)maxSubsequenceSumFirst:(NSArray *)array
{
int subSum, maxSum, i, j, k;
NSInteger count = array.count;
maxSum = 0;
for (i = 0; i < count; i++) {
for (j = i; j < count; j++) {
subSum = 0;
for (k = i; k <= j; k++) {
subSum += [array[k] intValue];
}
if (subSum > maxSum) {
maxSum = subSum;
}
}
}
return maxSum;
}
稍后一点经验的开发者,都可以看出最内层的for循环,其实有点多余,是可以省略的。因此就有了算法2。
算法2
算法2是在算法1的基础上做了一些优化,也比较简单,因此就不做介绍了。
- (int)maxSubsequenceSumSecond:(NSArray *)array
{
int subSum, maxSum, i, j;
NSInteger count = array.count;
maxSum = 0;
for (i = 0; i < count; i++) {
subSum = 0;
for (j = i; j < count; j++) {
subSum += [array[j] intValue];
if (subSum > maxSum) {
maxSum = subSum;
}
}
}
return maxSum;
}
算法3
算法3采用一种分治策略。分治策略就是把问题分成两个大致相等的子问题,然后递归地对它们求解,这是分的部分。治阶段就是将两个子问题的解合并到一起并可能再做少量工作,最后得到整个问题的解。
该算法需要有一些分析:
在例子中,最大子序列和可能出现在三处。数据的左半部分,数据的右半部分,或者跨越数据的中部,左右两半部分各占一些。前两种情况可以用递归求解。第三种情况,需要加入一些计算,可以通过求出前半部分包含最后一个元素的最大和,后半部分包含第一个元素的最大和,然后将这两个和加在一起。
- (int)maxSubsequenceSumThird:(NSArray *)array{
int right = (int)array.count - 1;
return [self maxSubSum:array left:0 right:right];
}
- (int)maxSubSum:(NSArray *)array left:(int)left right:(int)right
{
int maxLeftSum, maxRightSum;
int maxLeftBorderSum, maxRightBorderSum;
int leftBorderSum, rightBorderSum;
int center, i;
if (left == right) { //基本情况,左右相同,说明只有一个元素 if (array[left] > 0) {
return [array[left] intValue];
} else {
return 0;
}
}
center = (left + right ) / 2;
maxLeftSum = [self maxSubSum:array left:left right:center];
maxRightSum = [self maxSubSum:array left:center + 1 right:right];
maxLeftBorderSum = 0;
leftBorderSum = 0;
for (i = center; i >= left; i--) {
leftBorderSum += [array[i] intValue];
if (leftBorderSum > maxLeftBorderSum) {
maxLeftBorderSum = leftBorderSum;
}
}
maxRightBorderSum = 0;
rightBorderSum = 0;
for (i = center + 1; i <= right; i++) {
rightBorderSum += [array[i] intValue];
if (rightBorderSum > maxRightBorderSum) {
maxRightBorderSum = rightBorderSum;
}
}
int max = MAX(maxLeftSum, maxRightSum);
return MAX(maxLeftBorderSum + maxRightBorderSum, max);
}
算法4
算法4也比较简短,但是算法4必须要大量思考。
分析:该算法首先定义两个变量,maxSum用来记录当前求出的最大子序列和,subSum用来记录遍历的元素中非零和。如果subSum小于0,就将subSum重置为0,因为后面即使是正数,也比不加上这个负数和要大。当出现subSum比之前记录的maxSum大时,就将其赋值给maxSum。一直遍历到最后一个元素为止。
- (int)maxSubsequenceSumFourth:(NSArray *)array{
int subSum, maxSum, j;
subSum = maxSum = 0;
for(j = 0; j < array.count ; j++) {
subSum += [array[j] intValue];
if (subSum > maxSum) {
maxSum = subSum;
} else if (subSum < 0) {
subSum = 0;
}
}
return maxSum;
}
总结
优秀的算法,往往需要我们自己的思考和分析也更多。分析可以去掉一些不必要的计算,来减小运算时间。
算法4只对数据进行一次扫描,一旦Ai被读入并被处理,它就不再需要被记忆。
因此,如果数组在磁盘或磁带上,它就可以被顺序的读入,在主存中不必存储数组的任何部分。不仅如此,在任意时刻,算法都能对它已经读入的数据给出子序列问题的正确答案。就有这种特性的算法叫做联机算法。
仅需要常量空间并以线性时间运行的联机算法几乎是完美的算法。
实际运行时间
当数组中元素的个数为10的时候:
2016-06-24 16:35:29.510 PractiseProject[4195:185619] 数组中元素的个数:10
2016-06-24 16:35:29.510 PractiseProject[4195:185619] 算法一运行时间:1.7808e-05 秒,计算结果:23
2016-06-24 16:35:29.510 PractiseProject[4195:185619] 算法二运行时间:5.098e-06 秒,计算结果:23
2016-06-24 16:35:29.511 PractiseProject[4195:185619] 算法三运行时间:8.092e-06 秒,计算结果:23
2016-06-24 16:35:29.511 PractiseProject[4195:185619] 算法四运行时间:2.909e-06秒,计算结果:23
当数组中元素的个数为28的时候(从上图中,可以看到算法2和算法3在30左右时会出现拐点):
2016-06-24 16:36:20.751 PractiseProject[4217:186946] 数组中元素的个数:28
2016-06-24 16:36:20.751 PractiseProject[4217:186946] 算法一运行时间:0.000150832 秒,计算结果:114
2016-06-24 16:36:20.751 PractiseProject[4217:186946] 算法二运行时间:1.8889e-05 秒,计算结果:114
2016-06-24 16:36:20.751 PractiseProject[4217:186946] 算法三运行时间:1.808e-05 秒,计算结果:114
2016-06-24 16:36:20.752 PractiseProject[4217:186946] 算法四运行时间:3.782e-06 秒,计算结果:114
当数组中元素的个数为100的时候:
2016-06-24 16:37:21.658 PractiseProject[4234:187666] 数组中元素的个数:100
2016-06-24 16:37:21.663 PractiseProject[4234:187666] 算法一运行时间:0.00419705 秒,计算结果:1204
2016-06-24 16:37:21.663 PractiseProject[4234:187666] 算法二运行时间:0.000202042 秒,计算结果:1204
2016-06-24 16:37:21.663 PractiseProject[4234:187666] 算法三运行时间:6.589e-05 秒,计算结果:1204
2016-06-24 16:37:21.664 PractiseProject[4234:187666] 算法四运行时间:7.354e-06 秒,计算结果:1204
当数组中元素的个数为1000的时候:
2016-06-24 16:38:00.642 PractiseProject[4249:188454] 数组中元素的个数:1000
2016-06-24 16:38:04.816 PractiseProject[4249:188454] 算法一运行时间:4.1736 秒,计算结果:32133
2016-06-24 16:38:04.829 PractiseProject[4249:188454] 算法二运行时间:0.0124339 秒,计算结果:32133
2016-06-24 16:38:04.829 PractiseProject[4249:188454] 算法三运行时间:0.00054806 秒,计算结果:32133
2016-06-24 16:38:04.829 PractiseProject[4249:188454] 算法四运行时间:3.9842e-05 秒,计算结果:32133
当数组中元素的个数为10000的时候(吃饭30分钟回来后,算法1还未计算出结果):
2016-06-24 16:39:03.479 PractiseProject[4265:189178] 数组中元素的个数:10000
2016-06-24 16:38:04.816 PractiseProject[4249:188454] 算法一运行时间:NA,计算结果:未知
2016-06-24 16:39:04.714 PractiseProject[4265:189178] 算法二运行时间:1.23446 秒,计算结果:852859
2016-06-24 16:39:04.719 PractiseProject[4265:189178] 算法三运行时间:0.00523675 秒,计算结果:852859
2016-06-24 16:39:04.720 PractiseProject[4265:189178] 算法四运行时间:0.000379842 秒,计算结果:852859
当数组中元素的个数为100000的时候:
2016-06-24 16:40:36.132 PractiseProject[4284:190117] 数组中元素的个数:100000
2016-06-24 16:38:04.816 PractiseProject[4249:188454] 算法一运行时间:NA,计算结果:未知
2016-06-24 16:42:40.983 PractiseProject[4284:190117] 算法二运行时间:124.846 秒,计算结果:14896405
2016-06-24 16:42:41.046 PractiseProject[4284:190117] 算法三运行时间:0.0624209 秒,计算结果:14896405
2016-06-24 16:42:41.049 PractiseProject[4284:190117] 算法四运行时间:0.00294211 秒,计算结果:14896405
补充
生成随机整数数组的方法:
/** * 生成一个有count个元素的数组 * * @paramcount 个数 * * @return数组 */- (NSArray *)arrayWithCount:(NSInteger)count
{
NSMutableArray *array = [NSMutableArray arrayWithCapacity:count];
if (count <= 0) {
return array;
}
for (int i = 0; i < count; i++) {
int number = arc4random() % count;
int random = arc4random() % 2;
if (random == 0) {
number *= -1;
}
[array addObject:[NSNumber numberWithInt:number]];
}
return array;
}
统计运行时间的过程:
int n = 100;
NSArray *randomArray = [self arrayWithCount:n];
NSLog(@"数组中元素的个数:%d",n);
CFTimeInterval startTime = CACurrentMediaTime();
int one = [self maxSubsequenceSumFirst:randomArray];
CFTimeInterval endTime = CACurrentMediaTime();
NSLog(@"算法一运行时间:%g 秒,计算结果:%d", endTime - startTime, one);
startTime = CACurrentMediaTime();
int two = [self maxSubsequenceSumSecond:randomArray];
endTime = CACurrentMediaTime();
NSLog(@"算法二运行时间:%g 秒,计算结果:%d", endTime - startTime, two);
startTime = CACurrentMediaTime();
int three = [self maxSubsequenceSumThird:randomArray];
endTime = CACurrentMediaTime();
NSLog(@"算法三运行时间:%g 秒,计算结果:%d", endTime - startTime, three);
startTime = CACurrentMediaTime();
int four = [self maxSubsequenceSumFourth:randomArray];
endTime = CACurrentMediaTime();
NSLog(@"算法四运行时间:%g 秒,计算结果:%d", endTime - startTime, four);