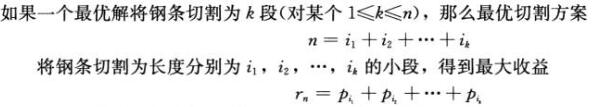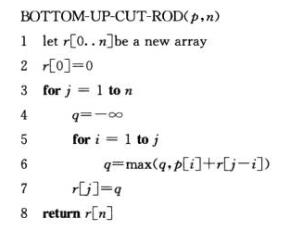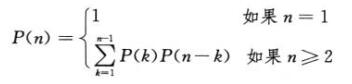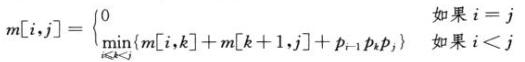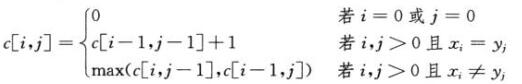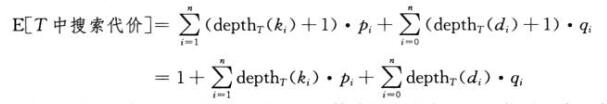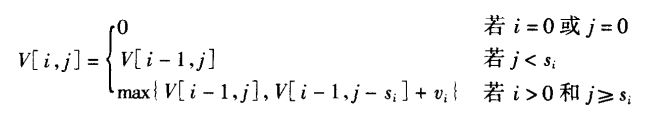动态规划

目录

• 1. 动态规划与分治法
• 2.动态规划求解的最优化问题应该具备的两个要素
  2.1 最优子结构
  2.2 子问题重叠
• 3. 动态规范的四个步骤
• 4. 实例
     4.1 钢条切割
     4.2 矩阵链乘法
     4.3 最长公共子序列
     4.4 最优二叉搜索树
     4.5 0-1背包问题
     参见0/1背包问题——动态规划、回溯、分支限界法对比
     4.6 旅行商问题
     参见旅行商(TSP)问题专题——多种方法对比
     4.7 所有结点对的最短路径问题
     参见最短路径专题

1. 动态规划与分治法

分治法将问题划分为互不相交的子问题，递归地求解子问题，再将它们组合起来，求出原问题的解。

动态规划应用于子问题重叠的情况，即不同的子问题具有公共的子子问题。动态规划对每个子子问题只求解一次，将其解保存在一个表格中。

2.动态规划求解的最优化问题应该具备的两个要素

2.1 最优子结构

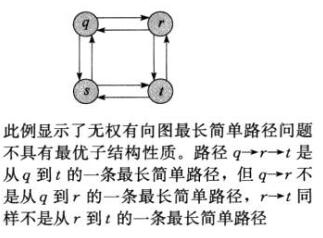
一个问题的最优解包含其子问题的最优解。（无权最长路径就不满足）
使用动态规划方法时，我们用子问题的最优解来构造原问题的最优解。

1.通用模式
发掘最优子结构的通用模式：
step1.证明问题的最优解的第一个组成部分是做出一个选择，例如，选择钢条第一次切割位置，选择矩阵链的划分位置等。做出选择会产生一个或多个待解决的子问题。
step2.对于一个给定的问题，在其可能的第一步选择中，你假定已经知道哪种才会得到最优解。
step3.给定可获得最优解的选择后，你确定这次选择会产生哪些子问题，以及如何最好地刻画子问题空间
step4.利用cut-and-paste技术证明：作为构成原问题最优解的组成部分，每个子问题的解就是它本身的最优解。

反证法：
假定子问题的解不是其自身的最优解，那么我们就可以从原问题的解中cut这些非最优解，将最优解paste进去，从而得到原问题的一个更优的解，这月最初的解是原问题的最优解的前提矛盾。

2.最优子结构的两个方面以及运行时间的估算
对于不同问题领域，最优子结构的不同体现在两个方面：
a.原问题的最优解设计多少个子问题
b.在确定最优解使用哪些子问题时，我们需要考察多少种选择

可以使用子问题的总数和每个子问题需要考虑多少种选择这两个因素的乘积来粗略分析动态规划的运行时间。

3.不具备最优子结构的例子
无权最短路径：找到一条从u到v的边数最少的路径（具有最优子结构性质）
无权最长路径：找到一条从u到v的边数最多的简单路径（不具备）

最长路径问题和最短路径问题的解都用到了两个子问题，但两个最长简单路径子问题是相关的，而两个最短路径字问题是无关的。
根本原因是：最短路径子问题间是不共享资源的。但是最长路径问题求解一个子问题用到了某些资源，导致这些资源在求解其他子问题时不可用。

2.2 子问题重叠

递归算法反复求解相同的子问题

3. 动态规范的四个步骤

step1. 刻画一个最优解的结构特征
step2. 递归地定义最优解的值
step3. 计算最优解的值，通常采用自底向上的方法
step4. 利用计算出的信息构造一个最优解
自顶向下的备忘方法优势在于：子问题空间中某些子问题完全不必求解，因为此种方法只会求解哪些绝对必要的子问题
自底向上的方法：没有递归调用的开销，表的维护开销也更小。

4. 实例

4.1 钢条切割

1）最优子结构与递归定义最优解的值
长度为n英寸的钢条总共有2的n-1次方种切割方案，因为每英寸的地方总可以选择切割或者不切割。

钢条切割问题满足最优子结构：问题的最优解由相关子问题的最优解组合而成，而这些子问题可以独立求解。（在所有可能的两段切割方案中选取组合效益最大者，构成原问题的最优解）

另一种更为简单的递归求解方法：将钢条从左边切割下长度为i的一段，只对右边剩下的长度为n-i的一段继续进行切割（递归求解），对左边一段则不再进行切割。

证明1.为什么第二种递归式也成立？

证明：r(i) + r(n - i)是重复的
a. r(1) + r(n - 1) 等于 p(1) + r(n - 1)
b. r(2) + r(n - 2) 可以分解为两个部分：
    p(2) + r(n - 2)以及 p(1) + p(1) + r(n -2)
    其中p(1) + p(1) + r(n - 2) 包含在a中
c.r(3) + r(n - 3)可以分解为：
   p(3) + r(n - 3)
   p(2) + r(1) + r(n-3) 包含在b
   p(1) + r(2) + r(n-3) 包含在a
...

简要说明如下：
对于左半边的分割在之前的遍历当中已经考虑到了，并不需要再考虑。
比如，如果从距离钢条左边2英寸处分割成两半然后只考虑右边的n-2英寸的钢条的分割的话，不需要考虑将左边2英寸的钢条再分为两个1英寸的情况；
因为在计算将左边分为一个1英寸这种情况的时，另外的n-1部分其中有一种情况就是将其分为一个1寸和n-2寸的情况，这样就考虑了之前所说的那种情况

2）自底向上计算最优解的值

3）利用计算出来的信息构造一个最优解
下面给出的是BOTTOM-UP-CUT-ROD的扩展版本，它对长队为j的钢条不仅计算最大收益指rj，还保存最优解对应的第一段钢条的切割长度sj：

构造最优解：

证明2：为什么构造最优解是正确的？

证明：
长度为j的最优切割为s[j] = i，那么这个i是不用切割的，只用去切割剩下的j - i
因此一直打印s[j]，然后再去切割j - s[j]

4.2 矩阵链乘法

完全括号化方案的数量：
当n = 1，由于只有一个矩阵，因此只有一种完全括号化方案
当n>=2，完全括号化的矩阵乘积可描述为两个完全括号化的部分积相乘的形式：

1）最优括号化方案的结构特征

2）一个递归求解方案
令m[i, j]表示计算矩阵Ai..j所需的标量乘法次数的最小值

3）计算最优代价

4）构造最优解

证明：构造最优解的方法是正确的

证明：
a.当i == j时，只有一个举证，直接打印
b.当i != j时，最外围打印( print1  print2)
    print1打印的是(s, i, k)
    pirnt2打印的是(s, k + 1, j)
    因为s[i, j] = k表示矩阵链从k处分为两个部分
因此是完全正确的

4.3 最长公共子序列

子序列的定义：一个给定的子序列，就是将给定序列中零个或多个元素去掉之后得到的结果。

1）LCS的最优子结构

2）一个递归解
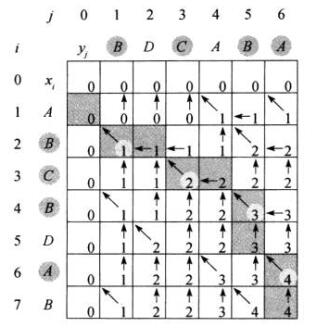
定义c[i, j]表示Xi和Yj的LCS的长度。

3）计算LCS的长度

4）构造LCS

正确性证明：
完全根据2）中公式进行，分为三种情况：

4.4 最优二叉搜索树

在给定单词出现频率的前提下，我们应该如何组织一颗二叉搜索树，使得所有搜索操作访问的结点总数最少。

1）最优子结构

g

2）一个递归算法

3）计算最优解

4.5 0-1背包问题

参见0/1背包问题——动态规划、回溯、分支限界法对比
1）问题的定义

2）最优子结构

g

3）递归算法

4）计算最优解

4.6 旅行商问题

参见旅行商(TSP)问题专题——多种方法对比

• 一个售货员必须访问n个城市，恰好访问每个城市一次，并最终回到出发城市。
  售货员从城市i到城市j的旅行费用是一个整数，旅行所需的全部费用是他旅行经过的的各边费用之和，而售货员希望使整个旅行费用最低。
• （等价于求图的最短哈密尔顿回路问题）令G=(V, E)是一个带权重的有向图，顶点集V=(v0, v1, ..., vn-1)。从图中任一顶点vi出发，经图中所有其他顶点一次且只有一次，最后回到同一顶点vi的最短路径。

4.6.1 刻画一个最优解的结构特征（最优子结构）

• 假设s₀s₁s₂...s_n，其中s₀=s_n，是一条从s₀出发的最短简单回路。
  那么有s_is_i+1...s_n也是从s_i出发，回到起点s_n的一条最短回路。（cut-and-paste证明）

4.6.2 递归地定义最优解的值（重叠子问题）

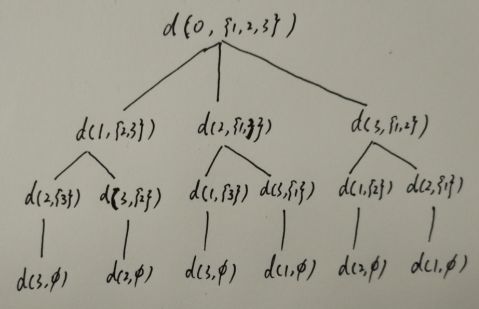
• 设TSP顶点编号为0,1,2,...,n-1.
  假设从顶点0出发
• d(i, V')定义为从顶点i出发经过V'中各顶点有且仅有一次，最后回到顶点0的最短路径长度
• c_ij定义为顶点i到顶点j的距离
  
  

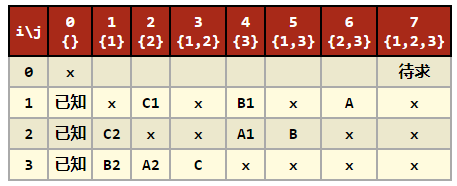
一个示例：

费用矩阵

递归求解子问题（重叠子问题）

4.6.3 计算最优解的值，通常采用自底向上的方法

• 假设顶点总数为n
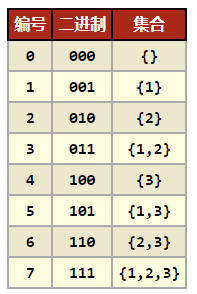
  则6.2中表的i范围是0 ≤ i ≤ n-1，j的范围是0 ≤ j ≤ 2^n-1 - 1

• 一个特别的规律：k表示第k-1位上是否为1，如下图所示

  
  
  

因此将一个集合转变成了一个数与之对应，数中对应的为位1，表示该数包含在集合中，否则，该数不在集合中。

按程序计算的表格

4.6.4 利用计算出的信息构造一个最优解

第一个打印0

4.7 所有结点对的最短路径问题

参见最短路径专题

• 所有结点对最短路径问题
  对于每对结点u和v，找到从结点u到结点v的最短路径。

• 基本方法和重复平方法——Θ(n⁴)和Θ(n³lgn)
  1）动态规划
  2）基本方法去掉一个不确定的边，需要遍历找到是哪个边
  3）重复平方法与基本方法的区别在于：基本方法到最终解，每次增加一条边；重复平方法每次增加一倍。

• Floyd-Warshall——Θ(n³)
  1）动态规划
  2）Floyd-Warshall去掉中间一个确定的点，不用遍历求最小