Python numpy中矩阵的用法总结

　　关于Python Numpy库基础知识请参考博文：https://www.cnblogs.com/wj-1314/p/9722794.html

Python矩阵的基本用法

　　mat（）函数将目标数据的类型转化成矩阵（matrix）

1，mat()函数和array()函数的区别

　　Numpy函数库中存在两种不同的数据类型（矩阵matrix和数组array），都可以用于处理行列表示的数字元素，虽然他们看起来很相似，但是在这两个数据类型上执行相同的数学运算可能得到不同的结果，其中Numpy函数库中的matrix与MATLAB中matrices等价。

　　直接看一个例子：

import numpy as np

a = np.mat('1 3;5 7')
b = np.mat([[1,2],[3,4]])
print(a)
print(b)
print(type(a))
print(type(b))
c = np.array([[1,3],[4,5]])
print(c)
print(type(c))

　　结果：

[[1 3]
 [5 7]]
[[1 2]
 [3 4]]


[[1 3]
 [4 5]]

　　首先，mat() 函数与array()函数生成矩阵所需的数据格式有区别，mat()函数中数据可以为字符串以分号（;）分割或者为列表形式以逗号（，）分割，而array()函数中数据只能为后者形式。

　　其次，两者的类型不同，用mat函数转换为矩阵后才能进行一些线性代数的操作。

from numpy import *

# 构建一个4*4的随机数组
array_1 = random.rand(4,4)
print(array_1)
print(type(array_1))
'''
[[0.12681561 0.26644355 0.03582107 0.71475804]
 [0.01380711 0.85308305 0.37838406 0.83663897]
 [0.20034209 0.5736587  0.56692541 0.64008518]
 [0.97780979 0.129229   0.37688616 0.55341492]]
 
 
 '''
# 使用mat函数将数组转化为矩阵
matrix_1 = mat(array_1)
print(matrix_1)
print(type(matrix_1))
'''
[[0.32538457 0.60674013 0.68625186 0.58957989]
 [0.26465813 0.93378939 0.12944934 0.95064032]
 [0.65683256 0.01352025 0.11932895 0.9361348 ]
 [0.11667241 0.16077876 0.50904118 0.44128675]]
 

'''

　　

 2，mat()函数创建常见的矩阵

import numpy as np

# 创建一个3*3的零矩阵，矩阵这里zeros函数的参数是一个tuple类型（3,3）
data1 = np.mat(np.zeros((3,3)))
print(data1)
'''
[[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]

'''
# 创建一个2*4的1矩阵，默认是浮点型的数据，如果需要时int，可以使用dtype=int
data2 = np.mat(np.ones((2,4)))
print(data2)
'''
[[1. 1. 1. 1.]
 [1. 1. 1. 1.]]
'''

# 这里使用numpy的random模块
# random.rand(2,2)创建的是一个二维数组，但是需要将其转化为matrix
data3 = np.mat(np.random.rand(2,2))
print(data3)
'''
[[0.62002668 0.55292404]
 [0.53018371 0.1548954 ]]
'''

# 生成一个3*3的0-10之间的随机整数矩阵，如果需要指定下界可以多加一个参数
data4  = np.mat(np.random.randint(10,size=(3,3)))
print(data4)
'''
[[0 4 1]
 [7 9 9]
 [9 0 4]]
'''

# 产生一个2-8之间的随机整数矩阵
data5 = np.mat(np.random.randint(2,8,size=(2,5)))
print(data5)
'''
[[4 6 3 3 4]
 [4 3 3 3 6]]
'''

# 产生一个2*2的对角矩阵
data6 = np.mat(np.eye(2,2,dtype=int))
print(data6)
'''
[[1 0]
 [0 1]]
'''
# 生成一个对角线为1,2,3的对角矩阵
a1 = [1,2,3]
a2 = np.mat(np.diag(a1))
print(a2)
'''
[[1 0 0]
 [0 2 0]
 [0 0 3]]
'''

　　

2.1，zeros

　　zeros函数是生成指定维数的全0数组

>>myMat=np.zeros(3)    ###生成一个一维的全0数组
>>print(myMat)
>>array([0.,0.,0.])


>>myMat1=np.zeros((3,2))  ####生成一个3*2的全0数组
>>print(myMat)
>>array([[0.,0.],
        [0.,0.]
        [0.,0.]])

　　

2.2，ones

　　ones函数是用于生成一个全1的数组

>>onesMat=np.ones(3)   ###1*3的全1数组
>>print(onesMat)
>>array([1.,1.,1.])



>>onesMat1=np.ones((2,3))   ###2*3的全1数组
>>print(onesMat1)
>>array([[1.,1.,1.],[1.,1.,1.]])

　　

2.3，eye

　　eye函数用户生成指定行数的单位矩阵

>>eyeMat=np.eye(4)  
>>print(eyeMat)
>>array([[1.,0.,0.,0.],
        [0.,1.,0.,0.],
        [0.,0.,1.,0.,],
        [0.,0.,0.,1.]])

　　

2.4，full

　　numpy.full(shape,fill_value=num)用于创建一个自定义形状的数组,可以自己指定一个值,用它填满整个数组。

　　fill_value 用来填充的值，可以是数字，也可以是字符串

nd_test = np.full(shape=(2,3,4),fill_value='ai')
print(nd_test)

array([[['ai', 'ai', 'ai', 'ai'],
        ['ai', 'ai', 'ai', 'ai'],
        ['ai', 'ai', 'ai', 'ai']],

       [['ai', 'ai', 'ai', 'ai'],
        ['ai', 'ai', 'ai', 'ai'],
        ['ai', 'ai', 'ai', 'ai']]], dtype=' 
 

　　

2.5 nonzero()

　　nonzero函数是numpy中用于得到数组array中非零元素的位置（数组索引）函数。它的返回值是一个长度为a.ndim（数组a的轴数）的元组，元组的每个元素都是一个整数数组，其值为非零元素的下标在对应轴上的值。

　　只有a中非零元素才会有索引值，那些零值元素没有索引值，通过a[nonzero(a)]得到所有a中的非零值。

import numpy as np

SS = [0,0,0,0]  
re = np.array(SS)
print(SS)
print(np.nonzero(re))
'''
[0, 0, 0, 0]
(array([], dtype=int64),)
'''

　　a是一维数组（索引1和索引2的位置上元素的值非零）

>>> import numpy as np
>>> a = [0,2,3]
>>> b = np.nonzero(a)
>>> b
(array([1, 2], dtype=int64),)
>>> np.array(b).ndim
2

　　a是多维数组

from numpy import *

b = array([[1,1,1,0,1,1],[1,1,1,0,1,0],[1,1,1,0,1,1]])
print(b)
c = nonzero(b)
print(c)
'''
[[1 1 1 0 1 1]
 [1 1 1 0 1 0]
 [1 1 1 0 1 1]]
(array([0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 2], dtype=int64), 
array([0, 1, 2, 4, 5, 0, 1, 2, 4, 0, 1, 2, 4, 5], dtype=int64))
'''

　　解释一下：矩阵 b中，b[0,0] b[0,1],b[0,2],b[0,4],b[0,5]，b[1,0],b[1,1],b[1,2],b[1,4],b[2,0],b[2,1],b[2,2],b[2,4],b[2,5]元素的值非零。

　　当使用布尔数组直接作为下标对象护着元组下标对象中有布尔数组时，都相当于用nonzero()将布尔数组转换成一组整数数组，然后使用整数数组进行下标计算。

　　nonzero(a)返回数组a中值不为零的元素的下标，它的返回值是一个长度为a.ndim（数组a的轴数）的元组，元组的每个元素都是一个整数数组，其值为非零元素的下标在对应轴上的值。例如对于1维布尔数组b1，nonzero(b1)所得到的是一个长度为1的元组，它表示b1[0]和b1[2]的值不为0（FALSE）。

import numpy as np

b1 = np.array([True,False,True,False])
res1 = np.nonzero(b1)
print(res1)
# (array([0, 2], dtype=int64),)

　　对于二维数组b2，nonzero（b2）所得到的是一个长度为2的元组，它的第0个元素是数组a中值不为0的元素的第0个轴的下标，第一个元素则是第1轴的下标，因此从下面得到的结果可知b2[0,0] , n2[0,2]和b2[1,0]的值不为0：

b2 = np.array([[True,False,True],[True,False,False]])
res2 = np.nonzero(b2)
print(res2)
# (array([0, 0, 1], dtype=int64), array([0, 2, 0], dtype=int64))

　　当布尔数组直接做维下标时，相当于使用由nonzero()转换之后的元组作为下标对象：

b3 = np.arange(3*4*5).reshape(3,4,5)
res3 = b3[np.nonzero(b2)]
print(res3)
'''
[[ 0  1  2  3  4]
 [10 11 12 13 14]
 [20 21 22 23 24]]
'''

 

3，常见的矩阵运算

3.1，矩阵相乘（*）

　　就是矩阵的乘法操作，要求左边矩阵的列和右边矩阵的行数要一致

from numpy import  *
''' 1*2 的矩阵乘以2*1 的矩阵  得到1*1 的矩阵'''

a1 = mat([1,2])
print(a1)
a2 = mat([[1],[2]])
print(a2)
a3 = a1*a2
print(a3)
'''
[[1 2]]
[[1]
 [2]]
[[5]]
'''

　　

3.2，矩阵点乘（multiply）

　　矩阵点乘则要求矩阵必须维数相等，即M*N维矩阵乘以M*N维矩阵

from numpy import  *
''' 矩阵点乘为对应矩阵元素相乘'''

a1 = mat([1,1])
print(a1)
a2 = mat([2,2])
print(a2)
a3 = multiply(a1,a2)
print(a3)
'''
[[1 1]]
[[2 2]]
[[2 2]]
'''


a1 = mat([2,2])
a2 = a1*2
print(a2)
# [[4 4]]

3.3，矩阵求逆变换（.I）

from numpy import *
''' 矩阵求逆变换:求矩阵matrix([[0.5,0],[0,0.5]])的逆矩阵'''

a1 = mat(eye(2,2)*0.5)
print(a1)
a2 = a1.I
print(a2)
'''
[[0.5 0. ]
 [0.  0.5]]
[[2. 0.]
 [0. 2.]]
'''

　　

3.4，矩阵求转置（.T）

from numpy import *
'''矩阵的转置'''

a1 = mat([[1,1],[0,0]])
print(a1)
a2 = a1.T
print(a2)
'''
[[1 1]
 [0 0]]
[[1 0]
 [1 0]]
 '''

　　

3.5，求矩阵对应列行的最大值，最小值，和。

　　计算每一列，行的和

from numpy import *
'''计算每一列，行的和'''

a1 = mat([[1,1],[2,3],[4,5]])
print(a1)
#  列和，这里得到的是1*2的矩阵
a2=a1.sum(axis=0)
print(a2)
'''
[[7 9]]
'''
#  行和，这里得到的是3*1的矩阵
a3=a1.sum(axis=1)
print(a3)
'''
[[2]
 [5]
 [9]]
 '''
#  计算第一行所有列的和，这里得到的是一个数值
a4=sum(a1[1,:])
print(a4)
'''
5
'''

　　计算最大，最小值和索引

from numpy import *
'''计算每一列，行的和'''

a1 = mat([[1,1],[2,3],[4,5]])
print(a1)
'''
[[1 1]
 [2 3]
 [4 5]]
'''
#  计算a1矩阵中所有元素的最大值,这里得到的结果是一个数值
maxa = a1.max()
print(maxa)   #5
#  计算第二列的最大值，这里得到的是一个1*1的矩阵
a2=max(a1[:,1])
print(a2)   #[[5]]
#  计算第二行的最大值，这里得到的是一个一个数值
maxt = a1[1,:].max()
print(maxt)   #3
#   计算所有列的最大值，这里使用的是numpy中的max函数
maxrow = np.max(a1,0)
print(maxrow)   #[[4 5]]
# ;//计算所有行的最大值，这里得到是一个矩阵
maxcolumn = np.max(a1,1)
print(maxcolumn)
'''
[[1]
 [3]
 [5]]
'''
#  计算所有列的最大值对应在该列中的索引
maxindex = np.argmax(a1,0)
print(maxindex)   #[[2 2]]
#  计算第二行中最大值对应在改行的索引
tmaxindex = np.argmax(a1[1,:])
print(tmaxindex)  # 1

　

3.6，矩阵的分隔和合并　（vstack  hstack）

　　矩阵的分割，同列表和数组的分割一致

from numpy import *
''' 矩阵的分隔，同列表和数组的分隔一致'''

a = mat(ones((3,3)))
print(a)
# 分隔出第二行以后的行和第二列以后的列的所有元素
b = a[1:,1:]
print(b)
'''
[[1. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]
[[1. 1.]
 [1. 1.]]
'''

　　矩阵的合并

from numpy import *

a = mat(ones((2,2)))
print(a)
b = mat(eye(2))
print(b)
# 按照列和并，即增加行数
c = vstack((a,b))
print(c)
# 按照行合并，即行数不变，扩展列数
d = hstack((a,b))
print(d)
'''
[[1. 1.]
 [1. 1.]]
 
[[1. 0.]
 [0. 1.]]
 
[[1. 1.]
 [1. 1.]
 [1. 0.]
 [0. 1.]]
 
[[1. 1. 1. 0.]
 [1. 1. 0. 1.]]
'''

　　

3.7 数组叠加合并

• 列合并/扩展：np.column_stack()
• 行合并/扩展：np.row_stack()

a = np.array((1,2,3,4))
b = np.array((11,22,33,44))
res1 = np.column_stack((a,b))
res2 = np.row_stack((a,b))
print(a)
print(b)
print(res1)
print(res2)
'''
[1 2 3 4]
[11 22 33 44]
[[ 1 11]
 [ 2 22]
 [ 3 33]
 [ 4 44]]
[[ 1  2  3  4]
 [11 22 33 44]]
 '''

　　

3.8 数组均分（np.array.split()）

　　直接看例子：

x = np.arange(10)
res1 = np.array_split(x,2)
res2 = np.array_split(x,3)
print(res1)
print(res2)

'''
[array([0, 1, 2, 3, 4]), array([5, 6, 7, 8, 9])]
[array([0, 1, 2, 3]), array([4, 5, 6]), array([7, 8, 9])]
'''

　　

 

3.9，矩阵，列表，数组的转换

　　列表可以修改，并且列表中元素可以使不同类型的数据，如下：

li =[[1],'hello',3]

　　numpy中数组，同一个数组中所有元素必须为同一个类型，有几个常见的属性：

from numpy import *

a=array([[2],[1]])
print(a )
dimension=a.ndim
m,n=a.shape
# 元素总个数
number=a.size
print(number)
# 2
#  元素的类型
str=a.dtype
print(str)
# int32

　　numpy中的矩阵也有与数组常见的几个属性，他们之间的转换如下：

from numpy import *

# 列表
a1 = [[1,2],[3,2],[5,2]]
# 将列表转化为二维数组
a2 = array(a1)
# 将列表转化成矩阵
a3 = mat(a1)
# 将矩阵转化成数组
a4 = array(a3)
# 将矩阵转换成列表
a5=a3.tolist()
# 将数组转换成列表
a6=a2.tolist()
print(type(a1))
print(type(a2))
print(type(a3))
print(type(a4))
print(type(a5))
print(type(a6))
'''






'''

　　注意：当列表为一维的时候，将他们转换成数组和矩阵后，再通过tolist()转换成列表是不相同的，这里需要做一些小小的修改，如下：

from numpy import *

a1=[1,2,3]
print(a1)
print(type(a1))
a2=array(a1)
print(a2)
print(type(a2))
a3=mat(a1)
print(a3)
print(type(a3))
'''
[1, 2, 3]

[1 2 3]

[[1 2 3]]


'''
a4=a2.tolist()
print(a4)
print(type(a4))
a5=a3.tolist()
print(a5)
print(type(a5))
'''
[1, 2, 3]

[[1, 2, 3]]

'''

a6=(a4 == a5)
print(a6)
print(type(a6))
a7=(a4 is a5[0])
print(a7)
print(type(a7))
'''
False

False

'''

　　矩阵转换成数值，存在以下一种情况：

from numpy import *

dataMat=mat([1])
print(dataMat)
print(type(dataMat))
'''
[[1]]

'''

# 这个时候获取的就是矩阵的元素的数值，而不再是矩阵的类型
val=dataMat[0,0]
print(val)
print(type(val))
'''
1

'''

 

4,　matrix.getA()

　　getA()是numpy的一个函数，作用是将矩阵转成一个ndarray，getA()函数和mat()函数的功能相反，是将一个矩阵转化为数组。

　　如果不转，矩阵的每个元素将无法取出，会造成越界的问题，其具体解释如下：

matrix.getA()
 　　Return self  as an ndarray object.
　　Equivalent to np.asarray(self)
Parameters:  None
Returns:    __ret_: ndarray
           self  as an  ndarray

　　举例如下：

>>> x = np.matrix(np.arange(12).reshape((3,4))); x
matrix([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]])
>>> x.getA()
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

　　那么为什么需要转换呢？

　　因为在画出数据集合的函数中，代码如下（取自机器学习实战Logistic回归最佳拟合直线的函数）

def plotBestFit(weights):
    weights = weights.getA()
    ...
    for i in range(n):
        #分类
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i, 1])
            ycord1.append(dataArr[i, 2])
        else:
            xcord2.append(dataArr[i, 1])
            ycord2.append(dataArr[i, 2])

　　在这个代码，我们需要取出其中每一行每一列的值

如果是矩阵的话，我们测试一下：

>>> b
matrix([[1, 2, 3, 4],
        [1, 2, 3, 4],
        [1, 2, 3, 4],
        [1, 2, 3, 4]])
>>> b[1][1]
Traceback (most recent call last):
  File "", line 1, in 
  File "D:\Python\lib\site-packages\numpy\matrixlib\defmatrix.py", line 284, in __getitem__
    out = N.ndarray.__getitem__(self, index)
IndexError: index 1 is out of bounds for axis 0 with size 1
>>>
>>> len(b[1])
1
>>> len(b[1][0])
1

　　可以发现我们取出矩阵的一行大小只有1，如果你使用b[1][1]，b[1][2]之类的就会越界

　　当我们转为np.array类型时

>>> c
array([[1, 2, 3, 4],
       [1, 2, 3, 4],
       [1, 2, 3, 4],
       [1, 2, 3, 4]])
>>> len(c[1])
4
>>> c[1][1]
2
>>>

　　可以看出，我们可以取出任何一个值。

 

Python矩阵的切片

1，行操作

li = [[1,1],[1,3],[2,3],[4,4],[2,4]]
from numpy import *

a = [[1,2],[3,4],[5,6]]
a = mat(a)
# 打印整个矩阵
print(a[0:])
'''
[[1 2]
 [3 4]
 [5 6]]
 '''

# 打印矩阵E从1行开始到末尾行的内容
print(a[1:])
'''
[[3 4]
 [5 6]]  
'''

# 表示打印矩阵E 从1行到3行的内容
print(a[1:3])
'''
[[3 4]
 [5 6]]
 '''

　　

2，列操作

li = [[1,1],[1,3],[2,3],[4,4],[2,4]]
from numpy import *
mat = mat(li)
# 在整个矩阵的基础下，打印1列（指的是序列为1的列
print(mat[:,0])
'''
[[1]
 [1]
 [2]
 [4]
 [2]]
'''
# 在矩阵的1行到2行（[1,3)） 的前提下打印两列
# 2 列不是指两列，而是序号为2的列
print(mat[1:3,1])
'''
[[3]
 [3]]
 '''

　　

Python numpy库其他函数用法

Numpy 的tile函数用法

　　tile函数位于Python模块numpy.lib.shape_base中，他的功能是重复某个数组，比如 tile(A,reps)，功能是将数组A重复reps次，构成一个新的数组。

1，函数的定义与说明

　　函数格式为   tile(A,reps)

　　A和reps 都是array_like

　　A的类型众多，几乎所有类型都可以：array  list  tuple  dict  matrix 以及基本数据类型Int string  float 以及bool类型。

　　reps 的类型也很多，可以是tuple  list  dict  array int  bool  但不可以是float   string  matrix类型。

2，示例

  >>> a = np.array([0, 1, 2])
    >>> np.tile(a, 2)
    array([0, 1, 2, 0, 1, 2])
    >>> np.tile(a, (2, 2))
    array([[0, 1, 2, 0, 1, 2],
           [0, 1, 2, 0, 1, 2]])
    >>> np.tile(a, (2, 1, 2))
    array([[[0, 1, 2, 0, 1, 2]],
           [[0, 1, 2, 0, 1, 2]]])

    >>> b = np.array([[1, 2], [3, 4]])
    >>> np.tile(b, 2)
    array([[1, 2, 1, 2],
           [3, 4, 3, 4]])
    >>> np.tile(b, (2, 1))
    array([[1, 2],
           [3, 4],
           [1, 2],
           [3, 4]])

    >>> c = np.array([1,2,3,4])
    >>> np.tile(c,(4,1))
    array([[1, 2, 3, 4],
           [1, 2, 3, 4],
           [1, 2, 3, 4],
           [1, 2, 3, 4]])

　　

from  numpy import *

code1 = tile(1,2)
print(code1)
# [1 1]

code2 = tile((1,2,3),3)
print(code2)
# [1 2 3 1 2 3 1 2 3]

a = [1,3,4]
code3 = tile(a,[2,3])
print(code3)
'''
[[1 3 4 1 3 4 1 3 4]
 [1 3 4 1 3 4 1 3 4]]
 '''

　

Numpy数据类型转换astype dtype

1，查看数据类型

In [11]: arr = np.array([1,2,3,4,5])

In [12]: arr
Out[12]: array([1, 2, 3, 4, 5])

// 该命令查看数据类型
In [13]: arr.dtype
Out[13]: dtype('int64')

In [14]: float_arr = arr.astype(np.float64)

// 该命令查看数据类型
In [15]: float_arr.dtype
Out[15]: dtype('float64')

　　

2，转换数据类型

// 如果将浮点数转换为整数，则小数部分会被截断
In [7]: arr2 = np.array([1.1, 2.2, 3.3, 4.4, 5.3221])

In [8]: arr2
Out[8]: array([ 1.1   ,  2.2   ,  3.3   ,  4.4   ,  5.3221])

// 查看当前数据类型
In [9]: arr2.dtype
Out[9]: dtype('float64')

// 转换数据类型  float -> int
In [10]: arr2.astype(np.int32)
Out[10]: array([1, 2, 3, 4, 5], dtype=int32)

　　

3，字符串数组转换为数值型

In [4]: numeric_strings = np.array(['1.2','2.3','3.2141'], dtype=np.string_)

In [5]: numeric_strings
Out[5]: array(['1.2', '2.3', '3.2141'], dtype='|S6')

// 此处写的是float 而不是np.float64, Numpy很聪明，会将python类型映射到等价的dtype上
In [6]: numeric_strings.astype(float)
Out[6]: array([ 1.2, 2.3, 3.2141])

　　

Numpy  范数的用法

　　顾名思义，linalg = linear + algebralinalg = linear + algebra , norm则表示范数，首先需要注意的是范数是对向量（或者矩阵）的度量，是一个标量（scalar）：

　　np.linalg.norm(求范数):linalg=linear（线性）+algebra（代数）

　　首先：help(np.linalg.norm) 查看其文档：

norm(x, ord=None, axis=None, keepdims=False)

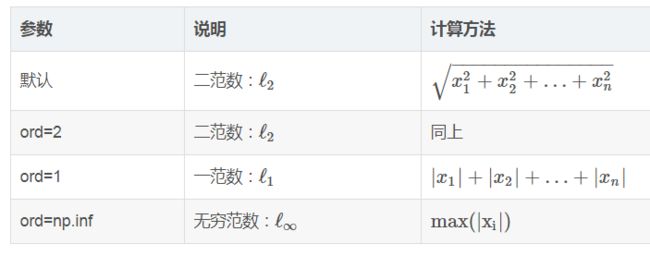
　　这里我们只对常用设置进行说明，x表示要度量的向量，ord表示范数的种类，axis表示向量的计算方向，keepdims表示设置是否保持维度不变。

用法：

import numpy as np

a=np.array([[complex(1,-1),3],[2,complex(1,1)]])  
print(a)


print(np.linalg.norm(a,ord=2) )   #计算矩阵2的范数


print(np.linalg.norm(a,ord=1) )   #计算矩阵1的范数


print(np.linalg.norm(a,ord=np.inf) )   #计算矩阵无穷的范数

　　

示例：

import numpy as np
x = np.array([5,7])
np.linalg.norm(x)
8.602325267042627
np.linalg.norm(x,ord=2)
8.602325267042627
np.linalg.norm(x,ord=1)
12.0
np.linalg.norm(x,ord=np.inf)
7.0

　　范数理论告诉我们，一范数 >=  二范数  >=  无穷范数

 

参考文献：https://blog.csdn.net/taxueguilai1992/article/details/46581861

https://blog.csdn.net/lanchunhui/article/details/51004387