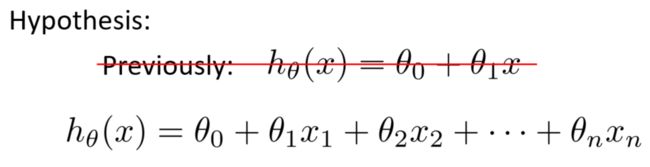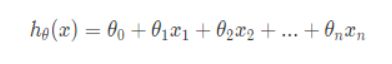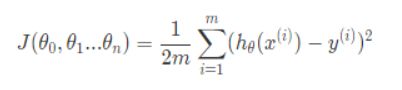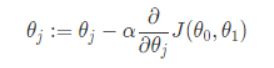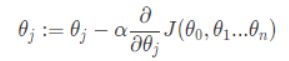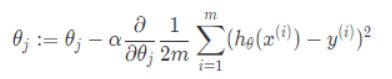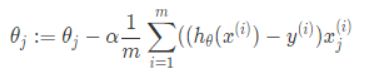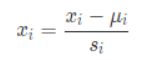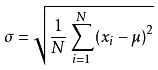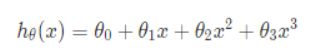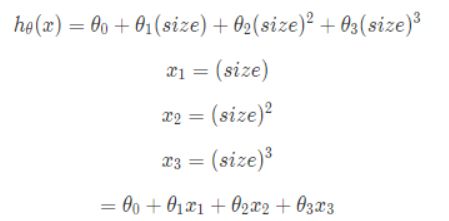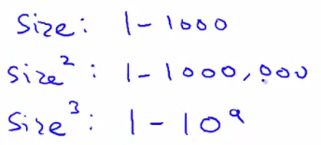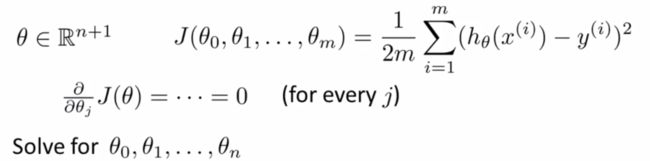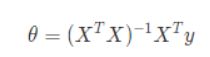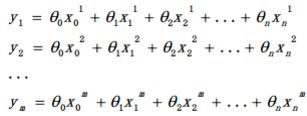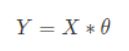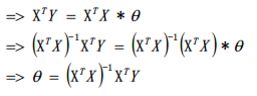1. 多变量线性回归(Linear Regression with Multiple Variables)
也称为多元线性回归,一元就是一个变量,多元就是多个变量,在这里也可以叫做多个特征
1.1 多维特征(Multiple Features)
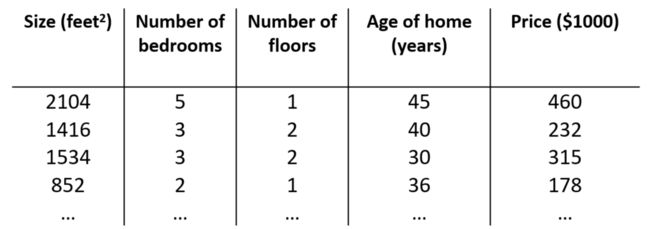
之前,我们讨论过单变量/特征的回归模型,但是单变量并不足以精确地预测房价,因此,我们需要对房价模型增加更多的特征,例如房间数楼层等,构成一个含有多个变量的模型。
现在需要引入新的注释来建立和解释新的模型↓
| 符号 | 意义 |
|---|---|
| i | 特征矩阵中的第 i 行 |
| j | 特征矩阵中第 i 行的第 j 个特征 |
| m | 训练样本的数量 |
| n | 特征的数量 |
在我们引入了新的特征之后,原来的那一条公式失去了作用,取而代之的是一条新的公式
多变量线性回归方程:
2. 多变量梯度下降(Gradient Descent for Multiple Variables)
2.1 代价函数
2.2 批量梯度下降算法
原公式:
经过修改,得到现在的公式:
代入多变量回归公式,得:
求导后得到批量梯度下降算法:
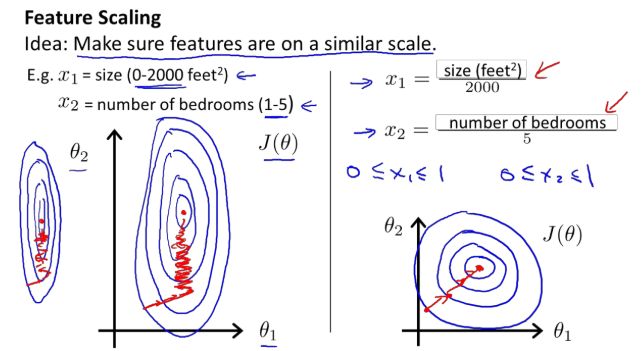
2.3 梯度下降法实践 1-特征缩放(Feature Scaling)
在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。
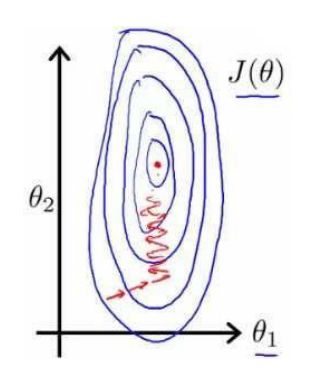
在以下图像中,我们就可以发现,图片非常地椭圆,这种椭圆使得我们在梯度下降的时候需要非常多次的迭代才能收敛。
因此我们需要特征缩放去解决这个问题,它将所有的特征尺度都尽量==缩放到-1到1之间==,太大或者太小都不好,如下图
2.3.1 特征均值标准化(mean normalization):
| 符号 | 含义 | 计算方法 | python(matlab)函数 | 参数解释 |
|---|---|---|---|---|
| x_i | 特征 | |||
| μ_i | 平均值 | 同一个x_n相加求再除以同一个x_n的数量 | python:mean(x,axis=0) matlab:mean(x) | x:数据集,axit:轴,为0计算每一列,为1计算每一行 |
| s_i | 标准差 | ,也可以简单的使用最大值减去最小值 | std(x) | 方法同上 |
2.4 梯度下降法实践 2-设置梯度下降法迭代次数(Debugging)
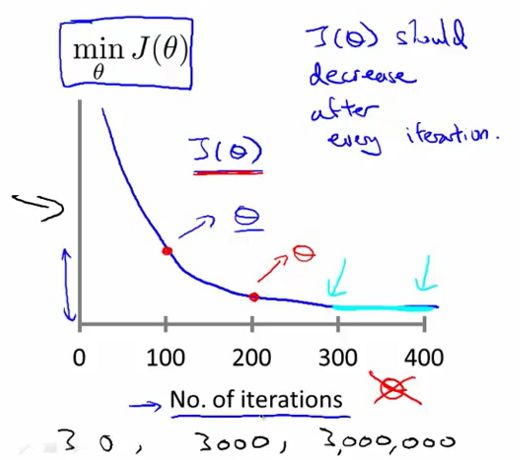
代价函数会随着迭代次数的下降而收敛,不同的迭代算法需要不同的迭代次数,有的可能需要30次,而有的可能则需要300万次
我们要判断代价函数是否收敛有两个方法
- 看代价函数的曲线变化
- 自动收敛测试
当下降幅度少于一个θ值的时候(θ值自己取),则可以看作代价函数收敛
但是一般而言,θ值是比较难确定的,最好还是自己通过图像去判断是否达到了收敛的程度
2.5 梯度下降法实践 3-学习率(Learning Rate)
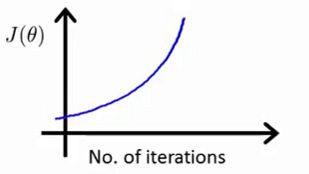
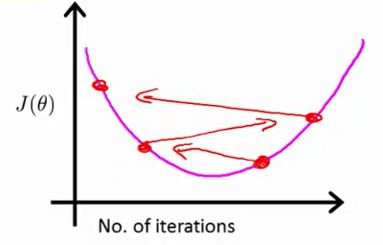
2.5.1 学习率α过大
通常,随着迭代次数的增加,代价函数应该是逐步下降的,但是当你看到代价函数的值增加的时候,很可能学习率过大所导致的,学习率过大使得函数错过了最低点
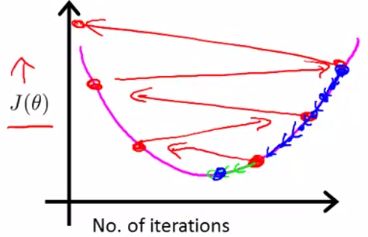
2.5.2 学习率α过小
学习率过大会有问题,那么过小了,也会造成问题,如下图的蓝色画笔所画,当学习率过小,学习速度就会很慢,需要更多的迭代次数才能迭代到最低点
2.5.3 如何选取学习率
在选取学习率的时候,我们通常都需要设置多个学习率进行测试,学习率之间的倍数通常是3倍和10倍,通过测试,我们就可以找到最好的那一个学习率
3. 特征与多项式回归(Features and Polynomial Regression)
首先我们来举一个例子:房价预测
| 符号 | 含义 |
|---|---|
| x1 | frontage(临街宽度) |
| x2 | depth(纵向宽度) |
| x | area(面积) |
由此,我们可以建立一个初步的模型
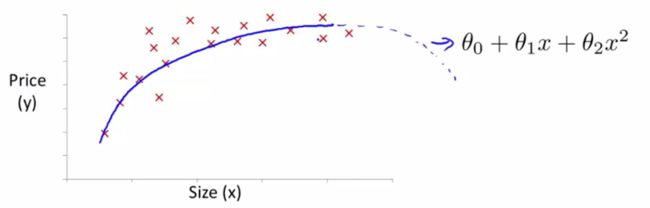
但是这个线性回归并不能很好的拟合我们的数据,因此我们需要一些改变(曲线)更好地拟合数据,比如一个二次方模型
如下图
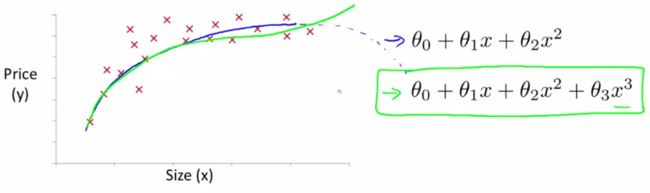
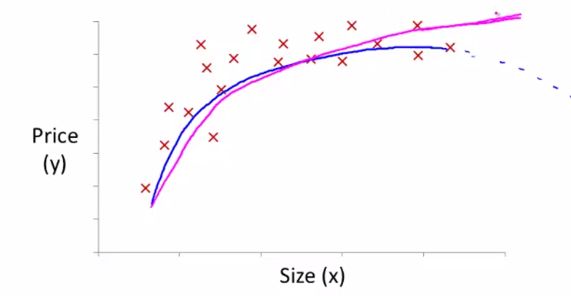
但是我们发现,二次方模型依然不能很好地拟合数据,因为它会随着Size的增加而下降,房价可不会因为房子面积的增加而下降,因此,我们需要一个三次方模型:
这样子,就可以比较好地拟合我们的数据
接下来,我们通过以下方法,将多项式回归转变为多元线性回归方程
这样子,就可以得到我们的多元线性回归方程
由此我们就可以得到3个特征,在读者看来,这可能是更好地标记特征,size和size的平方不是同一样东西
接下来还没完,我们发现特征与特征之间相差非常大
这就可能出现之前说过的迭代问题,因此,我们需要对特征进行缩放,从而使得方程能得到更好更快地迭代
当然,条条大路通罗马,除了三次方模型外,我们还可以采用其他模型使得曲线更加拟合数据,比如平方根模型(紫色线)
因此,我们需要深入了解数据和数据的本质,从而才能找到更好的模型去拟合数据
4. 正规方程(Normal Equation)
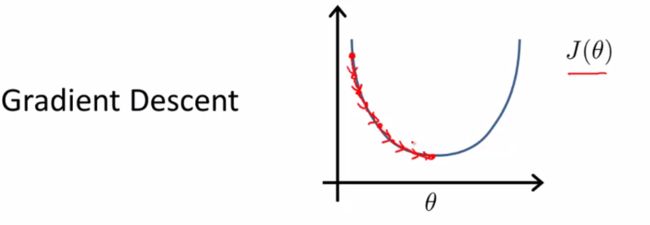
到目前为止,我们都在使用梯度下降算法求解最小值
但在某些问题上,用正规方程可以更快求解出最优值,通过正规方程可以一次性求到这一个值,那么什么是正规方程呢?
就拿上图的J(θ)函数来说,要求最优解,根据我们学过的微积分知识,对它进行一个直接求导就可以
回到之前说的平方代价函数,对于这么一个函数,我们需要对它每一个变量都进行求偏导,得出每一个θ的值
因此,我们选择使用线性代数的方法进行批量求导,使用以下正规方程就能解出向量θ
完整推导过程:
http://blog.xiangjiang.live/derivations-of-the-normal-equation/
https://zhuanlan.zhihu.com/p/22757336
先来理解一下这个方程
首先,假设样本数为m,每个样本的期望值与实际值y相等
转化成向量表达的形式
注:*符号是矩阵叉乘的意思
由于X不一定是方阵,所以X乘上X的逆不一定等于E(单位矩阵,就是对角线是1,其他为0的矩阵,单位矩阵肯定是一个方阵),因此X需要先乘上X的转置,使它变成一个方阵,由于一个方阵的逆乘一个方阵等于I(单位矩阵),所以就消去了,最后得到结果:
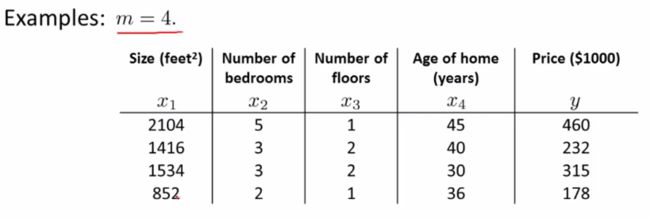
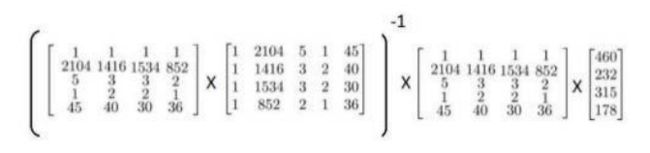
下面用数据来举一个例子
得到以下两个矩阵
运用正规方程方法求解,得
梯度下降与正规方程的比较:
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 α | 不需要 |
| 需要多次迭代 | 不需要迭代 |
| 当特征数量 n 大时也能较好适用 | 如果特征数量 n 较大则运算代价大,因为矩阵逆的计算时间复杂度为 O(n3),通常 来说当 n 小于 10000 时还是可以接受的 |
| 适用于各种类型的模型 | 只适用于线性模型,不适合逻辑回归模型等其他模型 |
总结一下,只要特征变量的数目并不大,正规方程是一个很好的计算参数 θ 的替代方法。具体地说,只要特征变量数量小于一万,我们通常使用标准方程法,而不使用梯度下降法。随着我们要讲的学习算法越来越复杂,例如,当我们讲到分类算法,像逻辑回归算法,我们会看到,实际上对于那些算法,并不能使用正规方程方法。
4.1 设计矩阵(design matrix)
统计学和机器学习中,设计矩阵是一组观测结果中的所有解释变量的值构成的矩阵,常用X表示。设计矩阵常用于一些统计模型,如一般线性模型,方差分析中。
4.2 矩阵X'X是奇异矩阵
原因有两个:
- 有两个成一定比例的特征值,使得矩阵不可逆
- 当训练样本比参数少很多的时候,可能会导致矩阵结果不可逆
解决方案:
- 查看特征里面是否有些重复或者多余的特征,比如呈线性相关的特征,删除重复两个重复特征中的其中一个
- 看特征值中是否有多余的特征,直到删到不再多余为止,如果实在太多,需要考虑使用正则化方法
如果矩阵 X' X是不可逆的,(通常来说,不会出现这种情况),如果在 Octave 里,可以用伪逆函数pinv()来实现。这种使用不同的线性代数库的方法被称为伪逆。即使X'X的结果是不可逆的,但算法执行的流程是正确的。总之,出现不可逆矩阵的情况极少发生,所以 在大多数实现线性回归中,出现不可逆的问题不应该过的关注 X' X 是不可逆的。