此文基于周莫烦大神@莫烦的视频,文章以及自己的一些心得。
1.3.1 性能衡量 Evaluation
Training/Validation/Test data
为了检验,评价神经网络, 避免和改善这些问题, 我们通常会把收集到的数据分为训练数据和测试数据,有时候还会分为训练数据,验证数据以及测试数据。 一般用于训练的数据可以是所有数据的70%, 剩下的30%可以拿来测试学习结果.如果你想问为什么要分开成两批, 那就想想我们读书时的日子, 考试题和作业题大部分都是不一样的吧. 这也是同一个道理.验证数据的作用就是你做完平常的作业题还不够,有时候老师还会给你加一些小测,你只有在小测的时候也能做的很好你才能参加最后的期末考试,也就是测试数据。
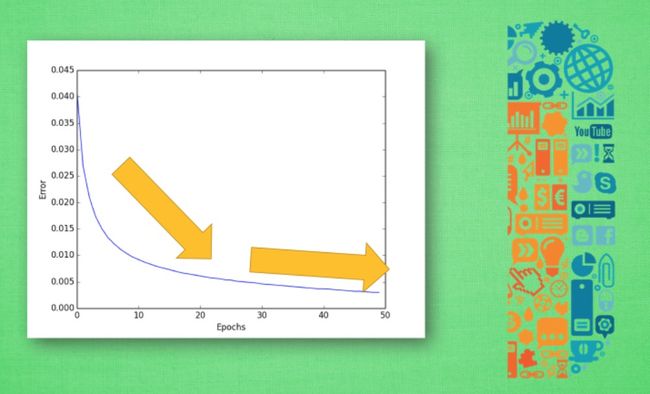
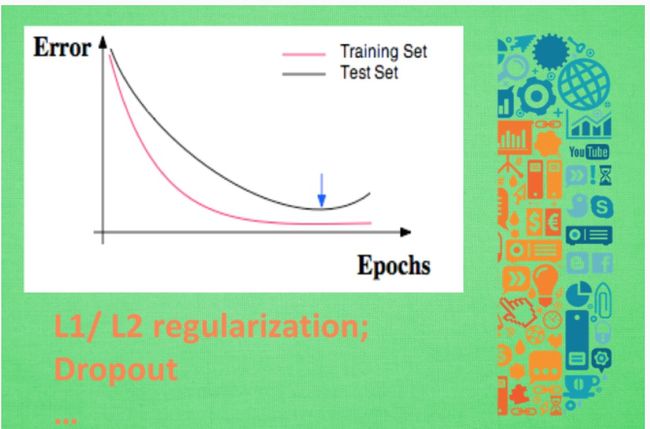
误差曲线
接着, 对于神经网络的评价基本上是基于这30%的测试数据. 想想期末考试虽然花的时间少, 但是占得总成绩肯定要比你平时作业的分多吧. 所以说这30%虽然少, 但是很重要. 然后, 我们就可以开始画图啦! 评价机器学习可以从误差这个值开始, 随着训练时间的变长, 优秀的神经网络能预测到更为精准的答案, 预测误差也会越少 . 到最后能够提升的空间变小, 曲线也趋于水平 . 班上的差生, 从不及格到80分已经不容易啦, 再往上冲刺100分, 就变成了更难的事了. 机器学习也一样. 所以, 如果你的机器学习的误差曲线是这样一条曲线, 那就已经是很不错的学习成果啦.
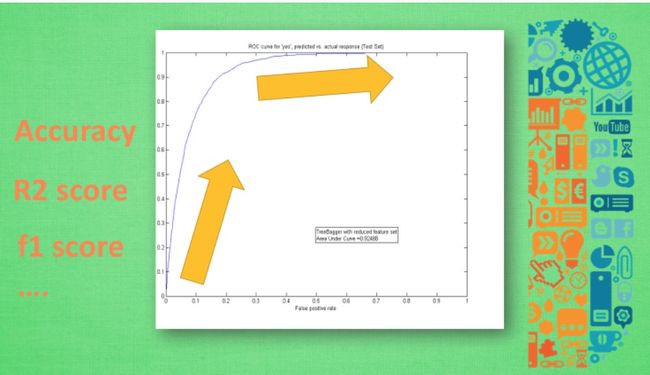
准确度曲线
同样, 除了误差曲线, 我们可以看他的精确度曲线. 最好的精度是趋向于100%精确. 比如在神经网络的分类问题中, 100个样本中, 我有90张样本分类正确, 那就是说我的预测精确度是90%. 不过, 不知道大家有没有想过对于回归的问题呢? 怎样看预测值是连续数字的精确度? 这时, 我们可以引用 R2 分数在测量回归问题的精度 . R2给出的最大精度也是100%, 所以分类和回归就都有的统一的精度标准. 除了这些评分标准, 我们还有很多其他的标准, 比如 F1 分数 , 用于测量不均衡数据的精度.
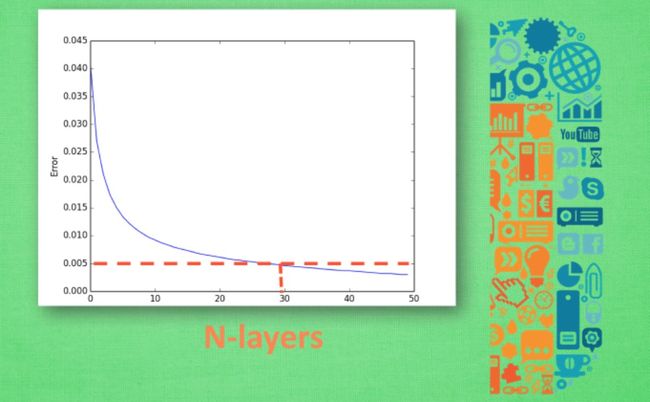
交叉验证 Cross-Validation
神经网络也有很多参数, 我们怎么确定哪样的参数能够更有效的解决现有的问题呢? 这时, 交叉验证 就是最好的途径了. 交叉验证不仅仅可以用于神经网络的调参, 还能用于其他机器学习方法的调参. 同样是选择你想观看的误差值或者是精确度, 不过横坐标不再是学习时间, 而是你要测试的某一参数 (比如说神经网络层数) . 我们逐渐增加神经层, 然后对于每一个不同层结构的神经网络求出最终的误差或精度, 画在图中. 我们知道, 神经层越多, 计算机所需要消耗的时间和资源就越多, 所以我们只需要找到那个能满足误差要求, 有节约资源的层结构. 比如说误差在0.005一下都能接受 , 那我们就可以采用30层的神经网络结构 .
1.3.2 过拟合 Overfitting
Overfitting是什么
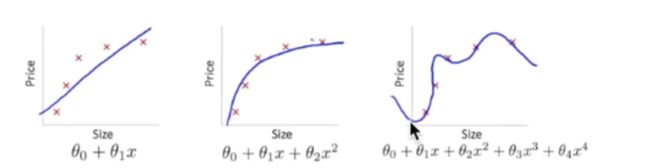
上面第三个图就是 overfitting,就是过度准确地拟合了历史数据,而对新数据预测时就会有很大误差。换句话来说,就是把训练集的数据学的太透彻了,以至于你在测试集上表现的很差。有时候, 意外是猝不及防的, 比如有时候我们明明每一道作业习题都会做, 可是考试分数为什么总是比作业分数低许多? 原来, 我们只复习了作业题,并没有深入, 拓展研究作业反映出来的知识. 这件事情发生在机器学习中, 我们就叫做过拟合. 我们在回到误差曲线, 不过这时我们也把训练误差画出来. 红色的是训练误差, 黑色的是测试误差. 训练时的误差比测试的误差小, 神经网络虽然学习到了知识, 但是对于平时作业太过依赖, 到了考试的时候, 却不能随机应变, 没有成功的把作业的知识扩展开来。
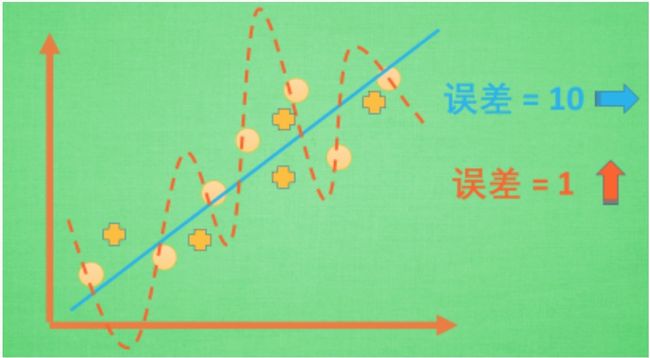
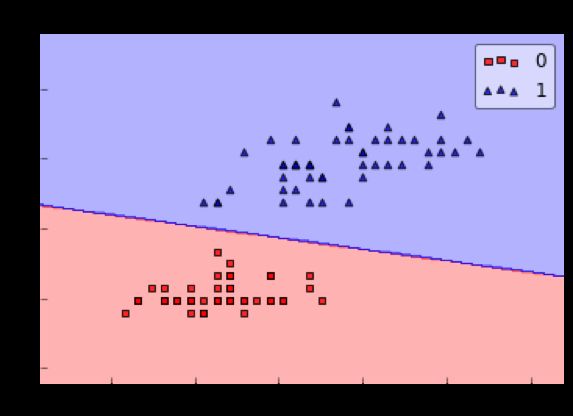
(1)过拟合在回归问题中的体现。这里是一些数据. 如果要你画一条线来描述这些数据, 大多数人都会这么画. 对, 这条线也是我们希望机器也能学出来的一条用来总结这些数据的线. 这时蓝线与数据的总误差可能是10. 可是有时候, 机器过于纠结这误差值, 他想把误差减到更小, 来完成他对这一批数据的学习使命. 所以, 他学到的可能会变成这样 . 它几乎经过了每一个数据点, 这样, 误差值会更小 . 可是误差越小就真的好吗? 看来我们的模型还是太天真了. 当我拿这个模型运用在现实中的时候, 他的自负就体现出来. 小二, 来一打现实数据 . 这时, 之前误差大的蓝线误差基本保持不变 .误差小的 红线误差值突然飙高 , 自负的红线再也骄傲不起来, 因为他不能成功的表达除了训练数据以外的其他数据. 这就叫做过拟合. Overfitting.
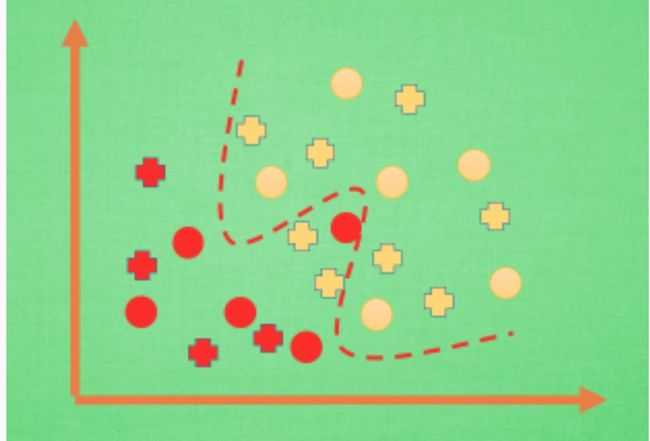
(2)过拟合在分类问题中的体现。在分类问题当中 . 过拟合的分割线可能是这样 , 小二, 再上一打数据 . 我们明显看出, 有两个黄色的数据并没有被很好的分隔开来. 这也是过拟合在作怪。
解决Overfitting的方法
1.增加数据量
大部分过拟合产生的原因是因为数据量太少了. 如果我们有成千上万的数据, 红线也会慢慢被拉直, 变得没那么扭曲。
2.L1&L2正则化(Regularisation)
运用正规化. L1, l2 regularization等等, 这些方法适用于大多数的机器学习, 包括神经网络. 他们的做法大同小异, 我们简化机器学习的关键公式为 y=Wx . W为机器需要学习到的各种参数. 在过拟合中, W 往往变化率比较大. 为了不让W一次性变化太大, 我们在计算误差上做些手脚. 原始的 cost 误差是这样计算 , cost = 预测值-真实值的平方. 如果 W 变得太大, 我们就让 cost 也跟着变大, 变成一种惩罚机制. 所以我们把 W 自己考虑进来 . 这里 abs 是绝对值. 这一种形式的 正规化, 叫做 l1 正规化. L2 正规化和l1 类似, , 只是绝对值换成了平方. 其他的l3.l4 也都是换成了立方和4次方等等. 形式类似. 用这些方法,我们就能保证让学出来的线条不会过于扭曲.
3. Dropout
还有一种专门用在神经网络的正规化的方法, 叫作 dropout. 在训练的时候, 我们随机忽略掉一些神经元和神经联结 , 是这个神经网络变得”不完整”. 用一个不完整的神经网络训练一次.到第二次再随机忽略另一些 , 变成另一个不完整的神经网络. 有了这些随机 drop 掉的规则, 我们可以想象其实每次训练的时候, 我们都让每一次预测结果都不会依赖于其中某部分特定的神经元. 像l1, l2正规化一样, 过度依赖的 W , 也就是训练参数的数值会很大, L1, L2会惩罚这些大的参数。Dropout 的做法是从根本上让神经网络没机会过度依赖。
1.3.3 特征标准化 (Feature Normalization)
什么是特征标准化
在说特征标准化之前, 我们先来说说现实生活中, 我们的数据是什么样的. 它们很可能来自不同的地方, 被不同的人采集, 有着不同的规格. 用最经典的房价预测例子来和大家说说. 我们用机器学习从房屋的各个层面来预测房价, 房屋的特征可能包括, 离市中心的距离, 房屋楼层, 房屋面积, 所在城市, 几室几厅等等. 这些数据的取值范围往往差距悬殊, 比如楼层一般在2-30层以内, 面积可能上百, 离市中心距离可以以千来记.
回到机器学习中, 如果我们以一个简单的线性回归方程来预测房屋的价格, 那方程可能会是这样 . 价格= a* 离市中心 + b * 楼层 + c * 面积. 其中的 a b c 就是机器学习需要努力努力再努力 来优化的参数.我们说的在具体一点, 用 abc 算出来的价格是预测价格 . 机器学习需要计算预测值和实际值的差别, 然后对这个误差进行一些数学上的处理, 使之变成进步的阶梯, 然后反向地传递回参数 a b c 来提升下次的预测准确度.
为了好理解, 我们把 b 先排除掉. 再把房价问题也简化一下, 留下两个特征. 因为面积的跨度一般可以从0 到 2-300, 而离市中心的距离跨度一般在10以内. 所以在这个公式中, c 只要稍稍变化一点, 他乘以面积的变化就会很大, 因为面积的值可以很大, 但是当a也变化那一点点时, 他对预测价格的影响力不会像 c 那样巨大. 这样的差别就会影响最终的工作效率. 所以, 我们要提高效率, 特征的标准化就可以帮上忙. 我们在机器学习训练之前, 先对数据预先处理一下, 取值跨度大的特征数据, 我们浓缩一下, 跨度小的括展一下, 使得他们的跨度尽量统一.
特征标准化的方法
通常用于特征标准化的途径有两种, 一种叫做 min max normalization, 他会将所有特征数据按比例缩放到0-1的这个取值区间. 有时也可以是-1到1的区间. 还有一种叫做 standard deviation normalization, 他会将所有特征数据缩放成 平均值为0, 方差为1. 使用这些标准化手段. 我们不仅可以快速推进机器学习的学习速度, 还可以避免机器学习学得特扭曲.
1.3.4 特征选取(Feature Selection)
为什么要进行特征选取
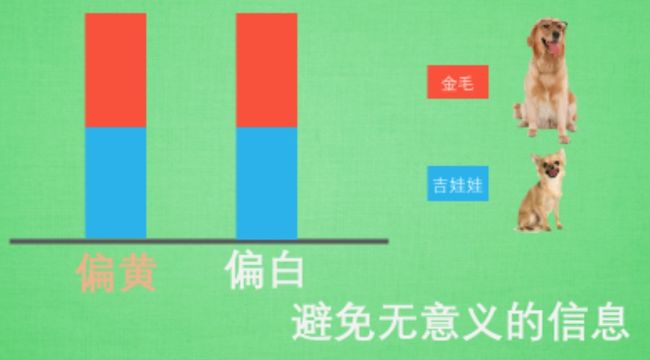
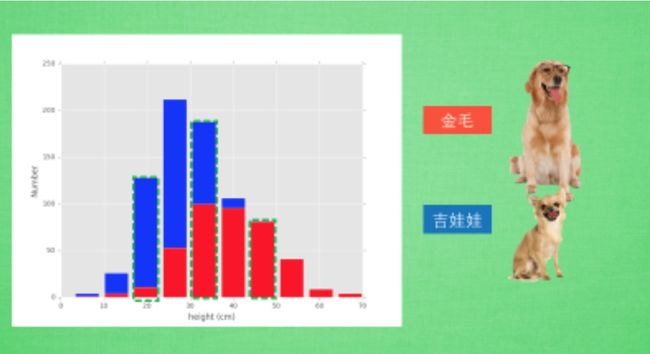
我们假设世界上的金毛和吉娃娃只有两种颜色, 偏黄, 偏白 . 然后我们用蓝色和红色分别代表吉娃娃和金毛所占的比例 . 如果在偏黄这边, 比例是这样 ,就可以说明, 在偏黄的方面, 吉娃娃和金毛所占的比例基本相同, 同样 , 如果偏白色的吉娃娃和金毛数量也基本相同. 这组数据就说明, 如果给你一个毛色是偏黄色的特征, 你是没有办法大概判断这只狗是吉娃娃还是金毛的. 这意味着. 通过毛色来观察这两种品种, 是不恰当的, 这个特征在区分品种上没有起到作用 . 那我们再换一个特征看看, 吉娃娃和金毛能不能用身高来分类呢?
我们拿这张图具体说说, 图里面有很多数据, 我们先举一这条来说明 , 可以看出, 在这组数据中, 如果给出高度50cm, 基本上我们就能够判定这只狗是金毛啦, 同样, 大于50cm 的, 都将是金毛. 当我们看到这一条数据 , 我们也可以有相当大的信心说, 在这个高度范围的, 很可能是只吉娃娃, 不过, 当我们再切换到这组数据 , 我们还能不能那么肯定地说这是那种狗呢? 这个高度范围, 因为两种狗都存在, 而且每种狗的数量都差不多, 所以在这个高度区间的狗狗我们就没办法判断. 所以高度是一个很有用的特征, 但是并不完美, 这就是我们为什么需要整合更多的特征来处理机器学习中的问题.
如何进行特征选取
避免无意义的信息
避免重复性的信息
避免复杂的信息
1.3.5 激励函数
为什么需要激励函数
激活函数的作用就是转换你的输入到不同的域使得其线性可分。
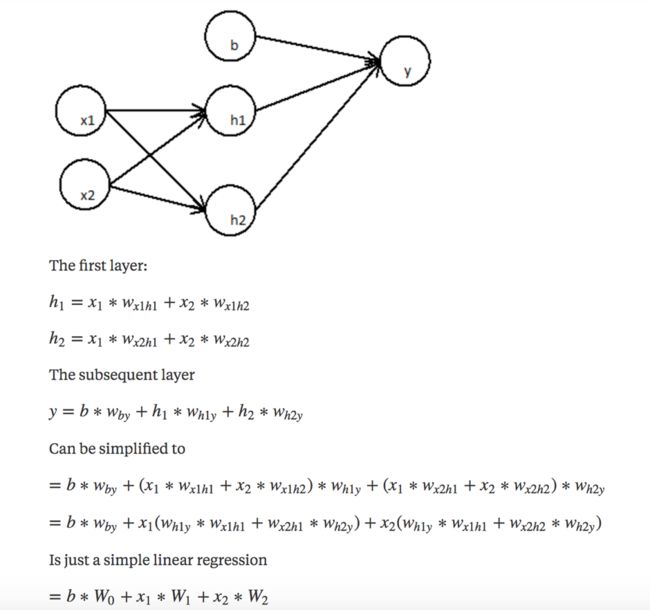
假设训练一个没有激活函数的多层神经网络,如下图:
由式子可以看出,如果没有使用激活函数,那么多层神经网络只是单纯的线性组合而已。
另外一个角度,尽管看起来似乎会太过琐碎,但我还是想先从「最初的地方」开始:线性回归(Linear regression)。
(常规的最小二乘法)线性回归的目的是找到最优权重——与输入线性组合——可得出一个能够最小化目标与解释变量之间垂直偏移的模型,但是在此我们并不会讨论模型拟合,因为这是另一个话题。
因此,在线性回归中,我们会计算权重与输入的线性组合(让我们把这个函数称为「净输入函数(net input function)」)。
net(x)=b+x1w1+x2w2+...xnwn= z
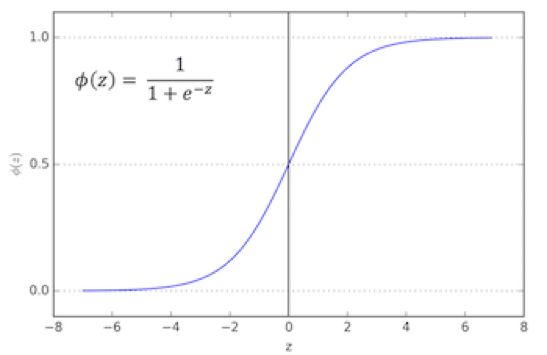
接下来,我们来讲逻辑回归(logistic regression)。我们让净输入量z通过一个非线性「激活函数(activation function)」——即逻辑S型函数(logistic sigmoid function)。
把它想象成线性的净输入量被「挤压」入一个拥有良好特性的非线性方程,可以返回条件概率P(y=1 | x)(即样本x隶属于类别1的概率)。现在,如果我们添加一个阶跃函数,例如:
如果S型函数输出大于或等于0.5预测为类别1,反之为类别0;
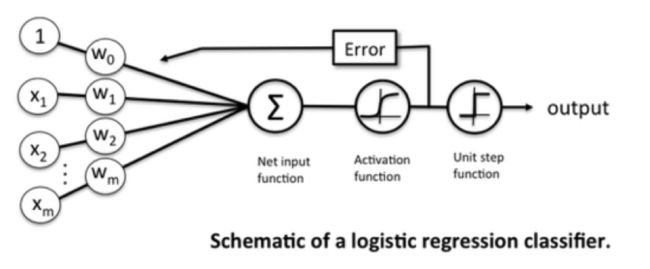
这样就可以得到如图所示的逻辑回归分类器:
但逻辑回归(一种泛化的线性模型)其决策面(decision surface)是线性的,从这个层面上来看它仍然是一种线性分类器:
如果数据类别可以线性划分,逻辑回归分类器对此可以工作的很好,但我们考虑一个棘手的例子
数据类别非线性可分。对于此处这个例子,一个非线性的分类器可能会是更好的选择,如一个多层神经网络。接下来,我训练了一个简单的多层感知器,其有一个包含200个这种逻辑S型激活函数的隐藏层。让我们从下图看一下现在决策面看起来是怎样的:
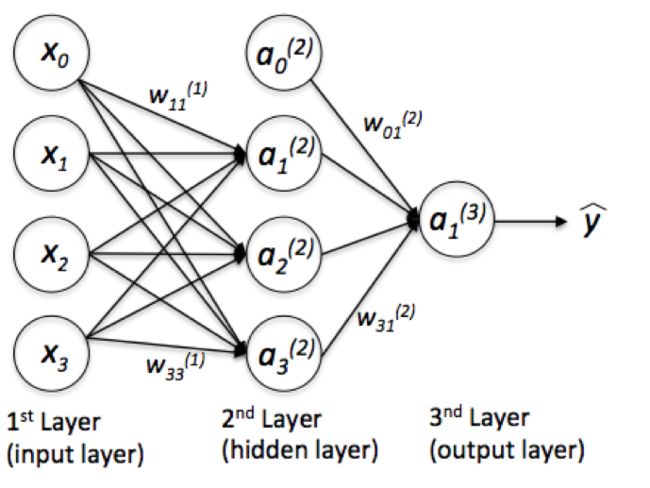
全连接的前馈神经网络,看起来基本如下图这样:
在这个特例中,我们的输入层只有3个单元(分别为x0= 1作为偏置单元,x1和x2作为两个特征);隐藏层有200个这样的S型激活函数(am),而输出层有一个S型函数。其之后被送入一个单位阶跃函数(图中没有展示)产生预测的输出类别标签y^。
总结一下,逻辑回归分类器有一个非线性激活函数,但是该模型的权重系数本质上是一个线性组合,也因此逻辑回归是一个泛化的线性模型。现在可以得到,激活函数在神经网络中的功能即通过对加权的输入进行非线性组合产生非线性决策边界(non-linear decision boundary)。
激活函数
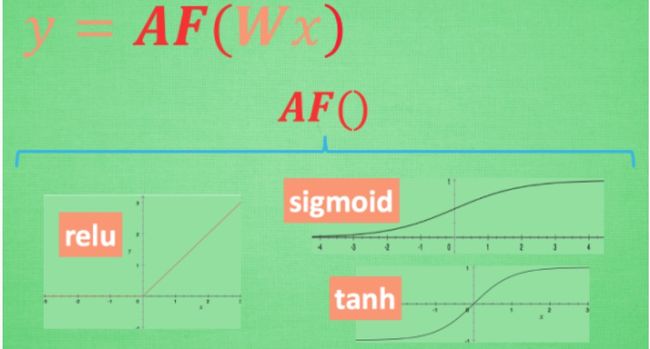
这里的 AF 就是指的激励函数. 激励函数拿出自己最擅长的”掰弯利器”, 套在了原函数上 用力一扭, 原来的 Wx 结果就被扭弯了.
其实这个 AF, 掰弯利器, 也不是什么触不可及的东西. 它其实就是另外一个非线性函数. 比如说relu, sigmoid, tanh. 将这些掰弯利器嵌套在原有的结果之上, 强行把原有的线性结果给扭曲了. 使得输出结果 y 也有了非线性的特征. 举个例子, 比如我使用了 relu 这个掰弯利器, 如果此时 Wx 的结果是1, y 还将是1, 不过 Wx 为-1的时候, y 不再是-1, 而会是0.
你甚至可以创造自己的激励函数来处理自己的问题, 不过要确保的是这些激励函数必须是可以微分的, 因为在 backpropagation 误差反向传递的时候, 只有这些可微分的激励函数才能把误差传递回去.
常用选择
想要恰当使用这些激励函数, 还是有窍门的. 比如当你的神经网络层只有两三层, 不是很多的时候, 对于隐藏层, 使用任意的激励函数, 随便掰弯是可以的, 不会有特别大的影响. 不过, 当你使用特别多层的神经网络, 在掰弯的时候, 玩玩不得随意选择利器. 因为这会涉及到梯度爆炸, 梯度消失的问题.
最后我们说说, 在具体的例子中, 我们默认首选的激励函数是哪些. 在少量层结构中, 我们可以尝试很多种不同的激励函数. 在卷积神经网络 Convolutional neural networks 的卷积层中, 推荐的激励函数是 relu. 在循环神经网络中 recurrent neural networks, 推荐的是 tanh 或者是 relu。
1.3.6 加速神经网络训练 (Speed Up Training)
Stochastic Gradient Descent
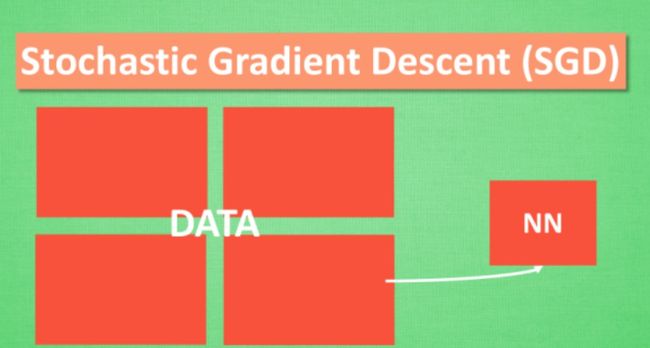
所以, 最基础的方法就是 SGD 啦, 想像红色方块是我们要训练的 data, 如果用普通的训练方法, 就需要重复不断的把整套数据放入神经网络 NN训练, 这样消耗的计算资源会很大.
我们换一种思路, 如果把这些数据拆分成小批小批的, 然后再分批不断放入 NN 中计算, 这就是我们常说的 SGD 的正确打开方式了. 每次使用批数据, 虽然不能反映整体数据的情况, 不过却很大程度上加速了 NN 的训练过程, 而且也不会丢失太多准确率.
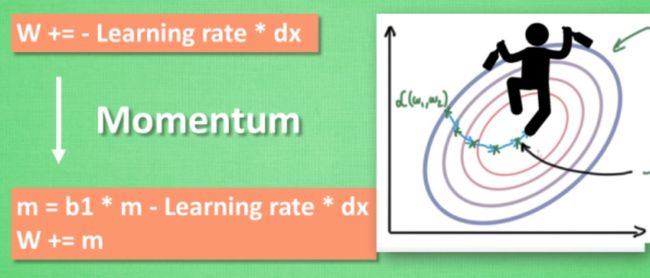
Momentum
大多数其他途径是在更新神经网络参数那一步上动动手脚. 传统的参数 W 的更新是把原始的 W 累加上一个负的学习率(learning rate) 乘以校正值 (dx). 这种方法可能会让学习过程曲折无比, 看起来像 喝醉的人回家时, 摇摇晃晃走了很多弯路.所以我们把这个人从平地上放到了一个斜坡上, 只要他往下坡的方向走一点点, 由于向下的惯性, 他不自觉地就一直往下走, 走的弯路也变少了. 这就是 Momentum 参数更新.
AdaGrad
这种方法是在学习率上面动手脚, 使得每一个参数更新都会有自己与众不同的学习率, 他的作用和 momentum 类似, 不过不是给喝醉酒的人安排另一个下坡, 而是给他一双不好走路的鞋子, 使得他一摇晃着走路就脚疼, 鞋子成为了走弯路的阻力, 逼着他往前直着走. 他的数学形式是这样的.
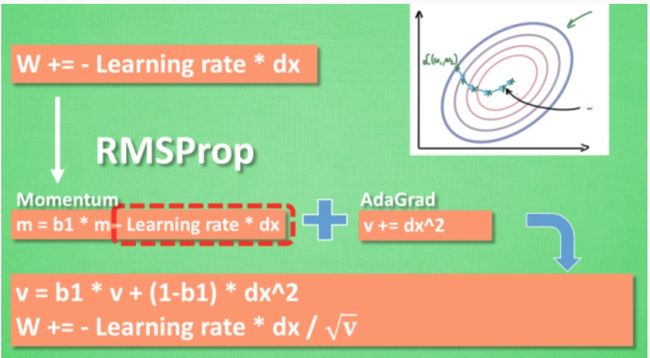
RMSProp
如果把下坡和不好走路的鞋子合并起来, 是不是更好呢?没错,这就是RMSProp.有了 momentum 的惯性原则 , 加上 adagrad 的对错误方向的阻力, 我们就能合并成这样. 让 RMSProp同时具备他们两种方法的优势. 不过细心的同学们肯定看出来了, 似乎在 RMSProp 中少了些什么. 原来是我们还没把 Momentum合并完全, RMSProp 还缺少了 momentum 中的 这一部分. 所以, 我们在 Adam 方法中补上了这种想法.
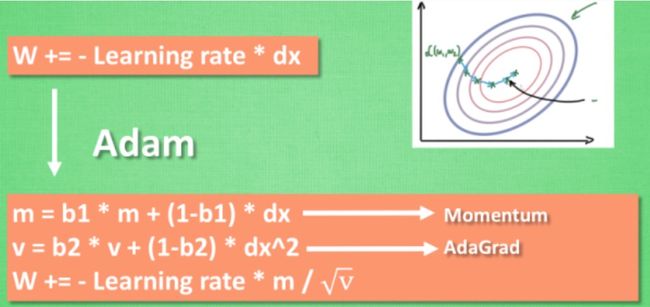
Adam
计算m 时有 momentum 下坡的属性, 计算 v 时有 adagrad 阻力的属性, 然后再更新参数时 把 m 和 V 都考虑进去. 实验证明, 大多数时候, 使用 adam 都能又快又好的达到目标, 迅速收敛. 所以说, 在加速神经网络训练的时候, 一个下坡, 一双破鞋子, 功不可没.
1.3.7 不均衡数据(Imbalanced data)
为什么不均衡数据会影响结果
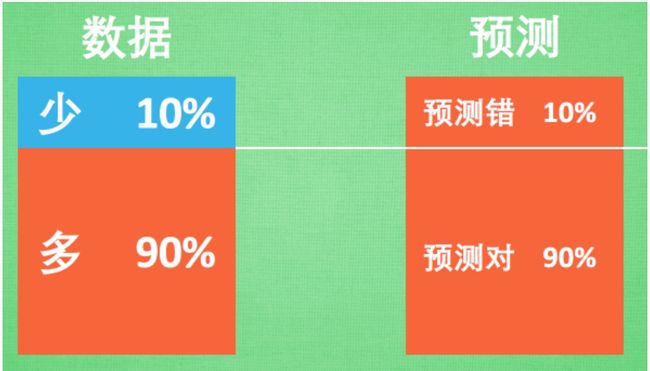
不均衡数据的形式很简单. 这里有1个苹果和9个梨, 当你发现你手中的数据对你说, 几乎全世界的人都只吃梨, 如果随便抓一个路人甲, 让你猜他吃苹果还是梨, 正常人都会猜测梨.
不均衡的数据预测起来很简单. 永远都猜多的那一方面准没错. 特别是红色多的那一方占了90%. 只需要每一次预测的时候都猜红色, 预测准确率就已经达到了相当高的90%了. 没错, 机器也懂这个小伎俩. 所以机器学到最后, 学乖了, 每次都预测多数派.
解决不均衡数据的方法
1.获取更多数据
首先, 我们要想想, 自己还能不能获取到更多的数据. 有时候只是因为前段时期的数据多半呈现的是一种趋势, 等到后半时期趋势又不一样了. 如果没有获取后半时期的数据, 整体的预测可能就没有那么准确了.
2.更换评判方式
通常, 我们会用到 准确率 accuracy, 或者误差 cost来判断机器学习的成果. 可是这些评判方法在不均衡数据面前, 高的准确率和低的误差变得没那么重要. 所以我们得换一种方式评判. 通过 confusion matrix 来计算 precision 和 recall, 然后通过 precision 和 recall 再计算f1 分数.这种方式能成功地区分不均衡数据, 给出更好的评判分数.
3.重组数据
第三种方法是最简单粗暴的方法之一. 重新组合不均衡数据, 使之均衡. 方式一: 复制或者合成少数部分的样本, 使之和多数部分差不多数量. 方式二: 砍掉一些多数部分, 使两者数量差不多.
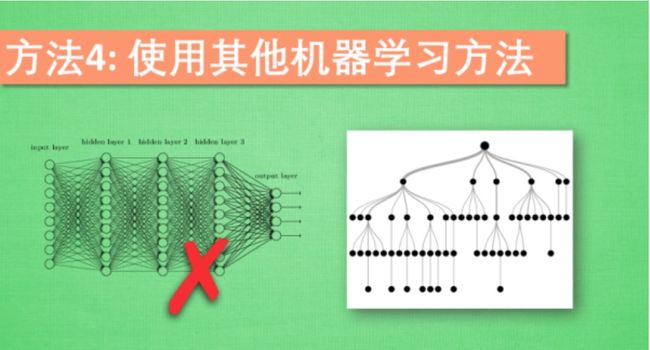
4.使用其他机器学习方法
如果使用的机器学习方法像神经网络等, 在面对不均衡数据时, 通常是束手无策. 不过有些机器学习方法, 像决策树, decision trees 就不会受到不均很数据的影响.
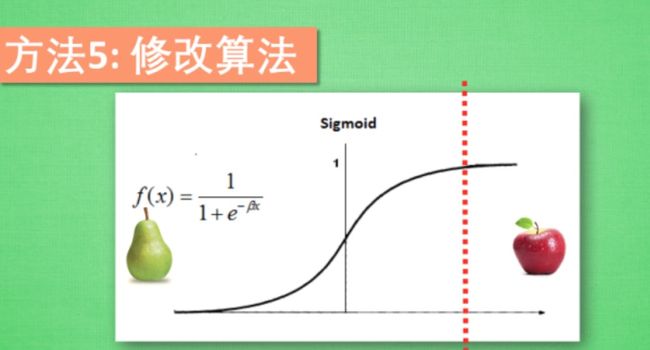
5.修改算法
尝试修改算法. 如果你用的是 Sigmoid 的激励函数, activation function, 他会有一个预测门槛, 一般如果输出结果落在门槛的这一段,预测结果为梨, 如果落在这一段, 预测结果为苹果, 不过因为现在的梨是多数派, 我们得调整一下门槛的位置, 使得门槛偏向苹果这边, 只有很自信的时候, 模型才会预测这是苹果. 让机器学习,学习到更好的效果.
1.3.8 不均衡数据(Imbalanced data)
Batch Normalization, 批标准化, 和普通的数据标准化类似, 是将分散的数据统一的一种做法, 也是优化神经网络的一种方法. 具有统一规格的数据, 能让机器学习更容易学习到数据之中的规律.
每层都做标准化
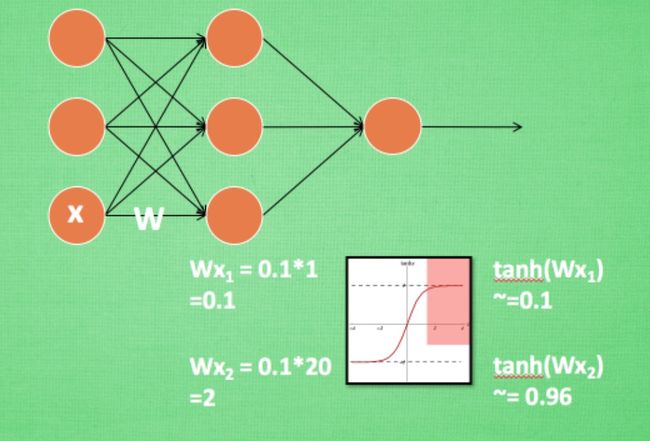
在神经网络中, 数据分布对训练会产生影响. 比如某个神经元 x 的值为1, 某个 Weights 的初始值为 0.1, 这样后一层神经元计算结果就是 Wx = 0.1; 又或者 x = 20, 这样 Wx 的结果就为 2. 现在还不能看出什么问题, 但是, 当我们加上一层激励函数, 激活这个 Wx 值的时候, 问题就来了. 如果使用 像 tanh 的激励函数, Wx 的激活值就变成了 ~0.1 和 ~1, 接近于 1 的部已经处在了 激励函数的饱和阶段, 也就是如果 x 无论再怎么扩大, tanh 激励函数输出值也还是 接近1. 换句话说, 神经网络在初始阶段已经不对那些比较大的 x 特征范围 敏感了. 这样很糟糕, 想象我轻轻拍自己的感觉和重重打自己的感觉居然没什么差别, 这就证明我的感官系统失效了. 当然我们是可以用之前提到的对数据做 normalization 预处理, 使得输入的 x 变化范围不会太大, 让输入值经过激励函数的敏感部分. 但刚刚这个不敏感问题不仅仅发生在神经网络的输入层, 而且在隐藏层中也经常会发生.
只是时候 x 换到了隐藏层当中, 我们能不能对隐藏层的输入结果进行像之前那样的normalization 处理呢? 答案是可以的, 因为大牛们发明了一种技术, 叫做 batch normalization, 正是处理这种情况.
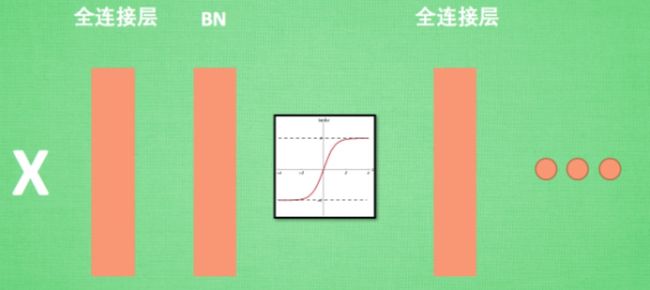
BN 添加位置
Batch normalization 的 batch 是批数据, 把数据分成小批小批进行 stochastic gradient descent. 而且在每批数据进行前向传递 forward propagation 的时候, 对每一层都进行 normalization 的处理。
BN 效果
Batch normalization 也可以被看做一个层面. 在一层层的添加神经网络的时候, 我们先有数据 X, 再添加全连接层, 全连接层的计算结果会经过 激励函数 成为下一层的输入, 接着重复之前的操作. Batch Normalization (BN) 就被添加在每一个全连接和激励函数之间。
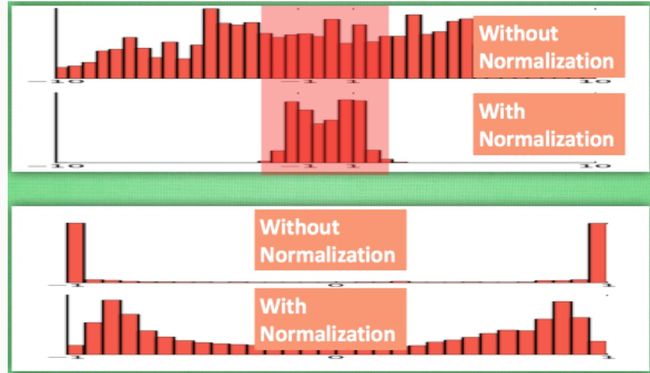
之前说过, 计算结果在进入激励函数前的值很重要, 如果我们不单单看一个值, 我们可以说, 计算结果值的分布对于激励函数很重要. 对于数据值大多分布在这个区间的数据, 才能进行更有效的传递. 对比这两个在激活之前的值的分布. 上者没有进行 normalization, 下者进行了 normalization, 这样当然是下者能够更有效地利用 tanh 进行非线性化的过程。
没有 normalize 的数据 使用 tanh 激活以后, 激活值大部分都分布到了饱和阶段, 也就是大部分的激活值不是-1, 就是1, 而 normalize 以后, 大部分的激活值在每个分布区间都还有存在. 再将这个激活后的分布传递到下一层神经网络进行后续计算, 每个区间都有分布的这一种对于神经网络就会更加有价值. Batch normalization 不仅仅 normalize 了一下数据, 他还进行了反 normalize 的手续. 为什么要这样呢?
BN 算法
我们引入一些 batch normalization 的公式. 这三步就是我们在刚刚一直说的 normalization 工序, 但是公式的后面还有一个反向操作, 将 normalize 后的数据再扩展和平移. 原来这是为了让神经网络自己去学着使用和修改这个扩展参数 gamma, 和 平移参数 β, 这样神经网络就能自己慢慢琢磨出前面的 normalization 操作到底有没有起到优化的作用, 如果没有起到作用, 我就使用 gamma 和 belt 来抵消一些 normalization 的操作.
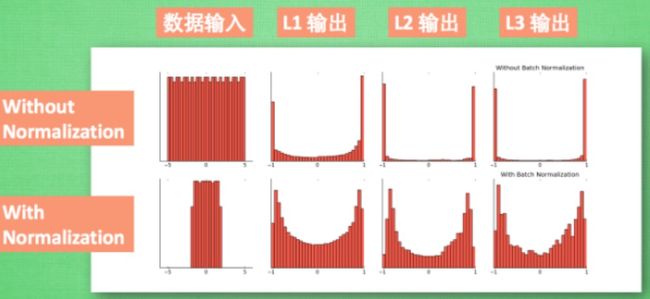
最后我们来看看一张神经网络训练到最后, 代表了每层输出值的结果的分布图. 这样我们就能一眼看出 Batch normalization 的功效啦. 让每一层的值在有效的范围内传递下去.