梯度下降算法
基于梯度的优化是优化一个函数的最终取值。输入参数,需要优化的函数是,基于梯度的优化即通过改变使得最大化或最小化,称为目标函数。
对于一元函数,它的导数记为,输入发生微小变化时,输出也发生变化,可以近似为
假设存在的足够小,则有,其中是符号函数。当小于0时,随着增加,减小,而当大于0时,随着减小,才能减小。的变化方向(+或者-)与导数的方向(正负)相反。
多元函数:方向导数与梯度的理解,参考博客https://www.cnblogs.com/wangguchangqing/p/10521330.html#autoid-0-0-0
方向导数
方向导数是指在某一点沿着某个方向的变化率,是一个==数值==。记为
自点引射线,与正轴方向的夹角为,与函数的交点,函数在的增量为,两点之间的距离。若沿着趋近于,如果增量与距离比值的极限存在,称该值为函数在处的方向导数,即公式(2)。
同时,若函数在处可微,则有,
两边同除以,可以得到
取极限得到
梯度
梯度是指是这样一个向量:每个元素为函数对一元变量的偏导数,它的大小即为最大方向导数。梯度记为
梯度与方向导数的联系:
设向量与同方向,根据方向导数的计算公式,有
其中表示梯度与向量的夹角,表示梯度的大小。可以看到,当方向向量与梯度同方向时,方向导数达到最大值,且最大值等于梯度的大小。
最大方向导数的等于梯度的模,,而梯度的方向由梯度向量与轴的角度给出,
由上述可得,函数在某点沿着梯度的方向增长最快,逆梯度方向减小最快。因此,要想求得函数的极小值(或最小值),可以通过沿逆梯度方向变化,不断下降找到极小值。
函数,则梯度为
梯度下降算法步骤
算法步骤:
给定目标函数和初始点位置
- 计算梯度,取反表示沿逆梯度方向。
- 计算下一处的值:每次参数移动的幅度是,称为学习率。更新后的参数
- 重复1、2,直至 ,其中是预先设置一个很小的值,满足条件时结束。
函数,它的梯度计算公式为初始位置,使用梯度下降计算极小值。其中学习率0.2。
计算过程如下
| 轮数 | 当前参数值 | 梯度取反 | 更新后的参数值 |
|---|---|---|---|
| 1 | 10 | -20 | 6.0 |
| 2 | 6.0 | -12.0 | 3.6 |
| 3 | 3.6 | -7.2 | 2.16 |
| 4 | 2.16 | -4.32 | 1.296 |
| 5 | 1.296 | -2.592 | 0.7776 |
| 6 | 0.7776 | -1.5552 | 0.466560 |
| 7 | 0.466560 | -0.933120 | 0.279936 |
| 8 | 0.279936 | -0.559872 | 0.167962 |
| 9 | 0.167962 | -0.335923 | 0.100777 |
| 10 | 0.100777 | -0.201554 | 0.060466 |
几种梯度下降算法
批梯度下降 batch gradient descent (BGD)
在每次参数更新时使用全部的样本数据,,优点是充分利用了全部数据,保证在足够多的的迭代后可以达到最优,缺点是数据量过大时迭代十分缓慢,收敛速度很慢。
随机梯度下降 stochastic gradient descent (SGD)
与BGD不同在于,每次使用一个样本用于更新参数。。优点是一次训练一个样本速度快,但一个样本决定梯度方向, 可能导致解不是最优,而且每次样本方向变化大,不容易很快收敛到最优解或局部最优解。
小批量梯度算法 Mini-batch gradient descent
每次使用一部分样本用于更新参数,即batch_size。对一个总样本数据m的数据集,每次使用x个样本,更新公式为
batch_size=1时,即为SGD的情况,batch_size=m时,即为BGD的情况。
梯度下降的缺陷
图片出自《深度学习与计算机视觉、算法原理、框架与代码实现》
函数的特殊点。从梯度下降的步骤来看,根据梯度的方向判断参数移动的方向,但是当的时候,就无法判断往哪边移动。称的点为驻点或者临界点。
函数会出现存在梯度为0的临界点,但该点不是最小点也不是最大点,这种临界点称为鞍点(Saddle Point)。
函数在某一段区域,梯度很小,且范围很大,梯度值小于更新条件,此时算法可能会停止迭代,这种区域称为停滞区。
极小值的存在,也会使算法停止迭代,从而得到不准确的结果,陷入局部最优解的情况。
因此,梯度下降算法的缺陷在于鞍点、停滞区、极小值的存在。
梯度下降算法通常适用于凸函数的情况。
梯度下降算法的改进
冲量momentum
算法步骤:
给定目标函数和初始点位置
- 计算梯度,取反表示沿逆梯度方向。
- 计算下一处的值:设置一个冲量项,,更新后的参数为
- 重复1、2。
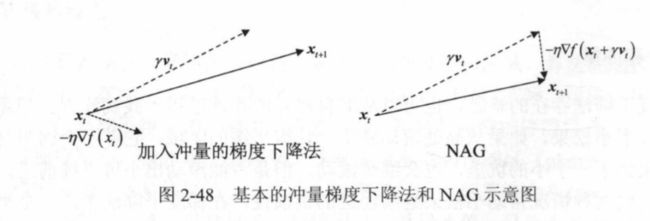
与原始梯度下降算法不一样的是,更新参数时,考虑到一个冲量,且冲量每次迭代时要乘以衰减数。在冲量项的影响下,算法迭代就相当于带上了“惯性”,前次迭代位置前进的方向可以影响到下一次迭代。这样当算法经过鞍点或是停滞区时,就不至于停下来做过于缓慢的迭代,而经过并不是很“深”的极值时,就可以借助冲量项带来的“惯性”冲出极值所的“坑”
算法停止的的标准也不再是梯度小于一个阈值。停止算法的标准可以是冲量小于某个值,梯度小于某个值,或是用户给定一个次数就停止。
Nesterov Accelerated Gradient Descent (NAG方法)
与加入冲量的改进唯一不同是,计算梯度的位置,不是当前位置,而是沿当前冲量前进一步的位置。
给定目标函数和初始点位置,以及初始动量
- 计算梯度,取反表示沿逆梯度方向。
- 计算下一处的值:设置一个冲量项,,更新后的参数为
- 重复1、2。
反向传播算法( BackPropagation算法 BP)
此部分参考了一篇博客,https://www.cnblogs.com/charlotte77/p/5629865.html,写的超级详细,跟着走了一遍过程,很容易理解反向传播的计算过程。
此外,参考《机器学习》的BP算法步骤,总结很简练,但没有具体数据去实现,看着很抽象。
算法的主要思想:
- 数据集输入神经网络,经过隐藏层,最终达到输出层。该过程是前向传播过程。
- 计算输出结果与真实结果存在误差,因此计算出误差,并将该误差从输出层向隐藏层反向传播,直至传播到输入层。
- 在反向传播的过程中,根据误差调整各种参数的值;不断迭代上述过程,直至收敛
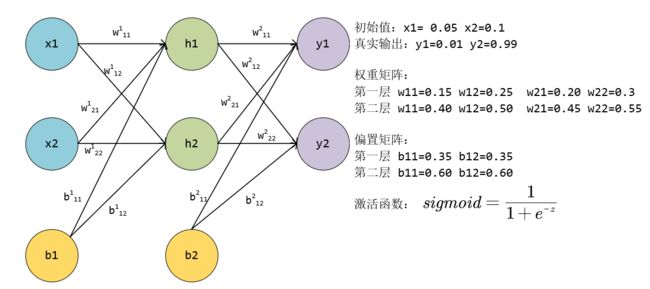
以下图为例,使用BP算法更新各层参数。
-
输入 计算各级的输出:
隐藏层输入
输入
隐藏层输出:
隐藏层到输出层:
神经元的输入输出是[1.10590596705977 0.7513650695523157]
神经元的输入输出是[1.2249214040964653 0.7729284653214625]
因此,前向传播的输出结果是 而真实值是
- 计算前向传播的结果与真实值的误差 ,使用均方误差
根据公式,可以算出总误差值
- 反向传播,更新参数。
误差的公式
误差公式中只有输出值是变量,每个输出值又是通过各个路径的参数“复合”而来,看成一个复合函数。以输出y1为例:,而等又可以推向输出层。
故
计算误差与某个参数的偏导,使用链式法则求偏导。
从输出层到隐藏层的参数
例如计算对最终损失的影响,偏导公式如下。没有考虑,因为的传播路径与无关。
依次计算该公式的各个部分的值。
对的偏导,
对的偏导,sigmoid函数的导数公式是。
根据计算式可以算出
对的偏导,计算式,可以算出
最后将三者乘起来,得到
更新的值,
其中是学习率,更新公式和梯度下降算法一样。
总误差对的偏导:
同理可得对的偏导。
更新后的参数
偏置更新:,中的偏置项只有一项,偏导是1。因此复合后的结果是
从隐藏层到输入层的参数更新
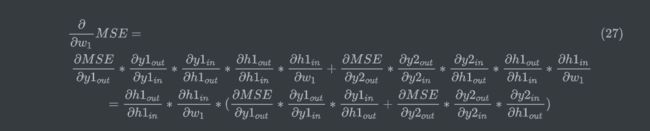
以为例,但是与上面不同的是,会影响到全部的输出,因为它通过传播到两个输出y,因此会有两个误差。(这段公式老是报错。。。只好贴图了)
如上图绿色箭头,每个神经元被分为两块,左边表示输入in,右边表示输出out,绿色表示反向传播的路径,截止到w1,可以看到,损失对w1的偏导,分为两条路径,但两条路径有部分是共用,即反向传播到输入层的部分。
公式(19)的计算过程如下,可以发现部分运算值已经在上面的w5到w8部分更新过一次。
而
同理可以算出
而
从而,公式(19)的括号里的值,计算结果是
计算到的偏导。从到,是一个sigmoid函数,而到输入是线性叠加,与有关的项是,因此对于的偏导是
综上,
更新的值,
同理,计算对的偏导。可以看到与计算不同的传播路径在于隐藏层到输入层是连接到这个神经元,因此
更新后w2的值是
同理计算w3和w4
更新后
也只有隐藏层反向到输出的位置不同,对,更新后
全部更新一轮后的输出结果为,损失由0.29837110876000270变降低到0.2812566048506621
总结:
这部分内容,在书上都放在了神经网络的优化方法部分。神经网络的训练实际上就是通过不断的训练,通过某种算法更新网络各个层级的权重参数,从而使损失函数降低。
梯度下降是通过函数的梯度性质来求解函数最小值,当然优缺点也很明显。除了梯度下降,还有牛顿-拉普森法、Adam法等很多其他优化算法。
而反向传播算法,是针对神经网络逆向优化所有参数,达到一个全局最优的解。