大学的时候不好好学习,老师在讲台上讲课,自己在以为老师看不到的座位看小说,现在用到了老师讲的知识,只能自己看书查资料进行再回炉学习,真心对不住老师,对不住父母,对不住自己的青春啊!
有些路,就是需要你自己走,有些知识就是需要你掌握,不论早几年还是现在还是几年后。。。是你的终归还是你的。。。
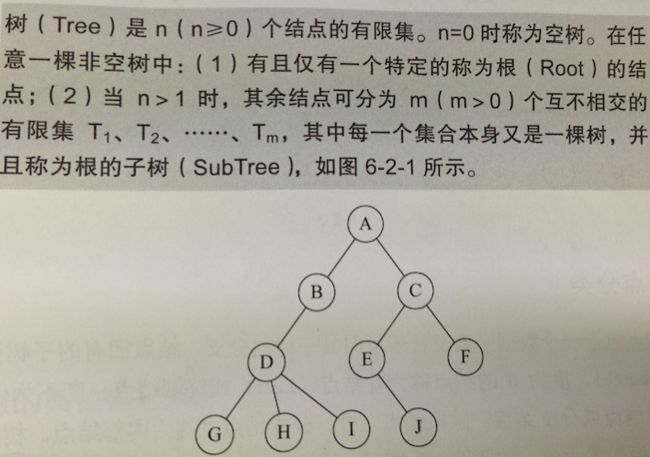
什么是树?
注意:
1、n>0时根结点是唯一的,不可能存在多个根结点。
2、m>0时子树的个数是没有限制的,但是它们一定是互不相交的。
1、结点的分类和度
结点拥有的子树数成为结点的度。
度为0的结点称为叶结点。
度不为0的结点称为分支结点。
处根结点外,分支结点也称为内部结点。
树的度是树内个结点的度的最大值。
简单理解就是每个结点的下一层有多少个结点,那么我们取这里面最大的那个,就是整个树的最大的度。上图中的树的结点的度的最大值是结点D的度=3,那么树的度也就是3。
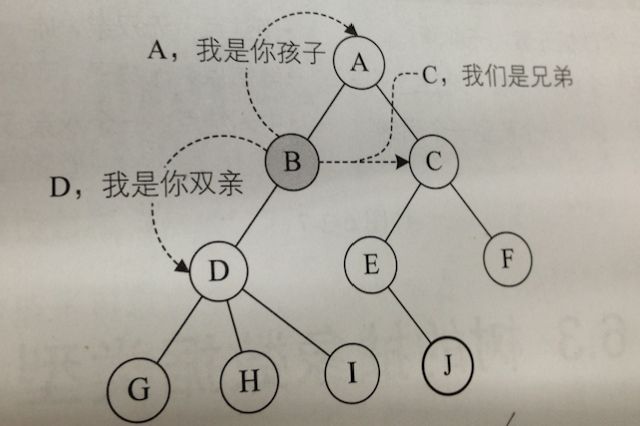
2、结点之间的关系
直接上图
结点的祖先是从根到该结点所经分支上的所有的结点。上图中,对H而言,D、B、A、都是H的祖先。
以某结点为根的子树中的任一结点都称为该结点的子孙。上图中,B的子孙有D、G、H、I。
3、树的其他概念
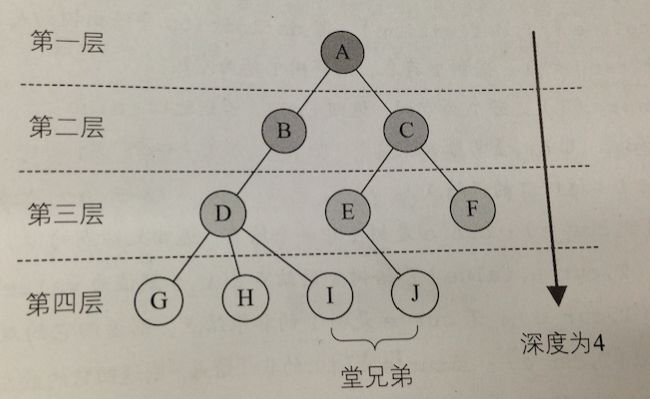
结点的层次从根开始定义起,根为第一层,依次下去。
在同一层的结点互为堂兄弟。
树中结点的最大层次称为树的深度或高度。(这个需要注意树的度和树的深度,不是一回事。)
如果将树的结点的各子树堪称从左到右是有次序的,不能互换的,则称该树为有序树,否则称为无序树。
线性结构和树结构的区别:
线性结构:第一个数据元素:无前驱。
最后一个数据元素:无后继。
中间元素:一个前驱一个后继。
树结构:根结点:无双亲,唯一。
叶结点:无孩子,可以多个。
中间结点:一个双亲多个孩子。
4、树的存储结构
双亲表示法
孩子表示法
孩子兄弟表示法
二叉树
树里面有很多结构,我们来研究最典型的。就像数有很多一样,正数负数有太多太多了,但是我们研究的也就是数轴周围的最多到一百或者一万,并不研究那些几个亿的数,因为我们通过一些典型的数据就能找到规律,另外我们平时用的话也就是这些典型的有规律的,无规律的一般不用也不进行研究,就像03年的“非典”,全名叫“非典型肺炎”,为什么开始的时候人们手足无措,因为是非典型的,不在我们平时的研究范围内啊,当然还有一些来势凶猛和传染等特性。
总之,我们这里研究的是树里面比较有规律的,比较典型的,从这些经典的树里面我们可以管中窥豹进一步的了解和学习树。
从上图中的红框中我们可以看出,二叉树的定义里面还用到了自己,这是递归啊!!!
1、二叉树的特点
每个结点最多有两棵子树,所以二叉树中不存在度大于2的结点,但是深度可以很大。
左子树和右子树是有顺序的,次序不能颠倒。
即使树中某结点只有一棵子树,也要区分它是左子树还是右子树。
二叉树的5中基本形态:
1、空二叉树。 (这能叫树吗?啥也没有。。。)
2、只有一个根结点的二叉树。 (这也能叫树吗?光杆司令一个。。。)
3、根结点只有左子树。 (这也好意思叫二叉?!没有右子树,你自己怎么叉啊?)
4、根结点只有右子树。
5、根结点既有左子树也有右子树。 (终于有一个正常的二叉树了。。。)
2、特殊的二叉树
二叉树就够特殊了,结果二叉树里面还有特殊的二叉树。。。
1、斜树。
所有的结点都只有左子树的二叉树叫左斜树。
所有的结点都只有右子树的二叉树叫右斜树。
(线性表结构可以理解为树的一种及其特殊的表现形式。。。还是树厉害啊!)
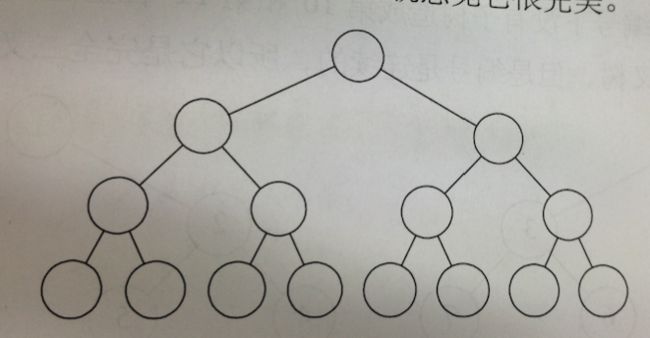
2、满二叉树。
在一棵二叉树中,如果所有的分支结点都存在左子树和右子树,并且所有的叶子都在同一层上,称为满二叉树。
感觉很完美。(前面的斜树们看看这里,你们也好意思叫二叉树?!你们都没劈叉。。。这才叫二叉树啊!!!泪流五分钟)
满二叉树的特点:
叶子只能出在最下一层。
非叶子结点的度一定是2。
在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多。
3、完全二叉树
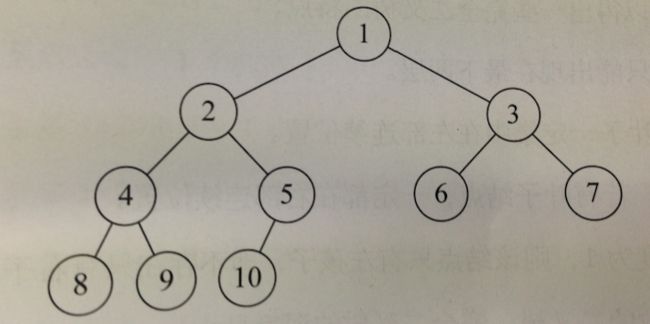
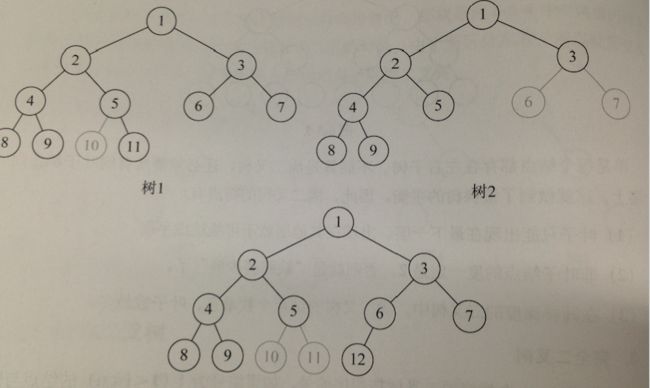
对于一棵具有n个结点的二叉树按层序编号,如果编号i(1<=i<=n)的结点与同样深度的满二叉树中的编号i的结点在二叉树中的位置完全相同,则这棵二叉树称为完全二叉树。
满二叉树一定是完全二叉树,完全二叉树不一定是满的。
下边的就不是完全二叉树,因为编号对不上!
完全二叉树的特点:
叶子的结点职能出现在最下两层。
最下层的叶子一定集中在左部连续位置。
倒数第二层,如果有叶子结点,一定是在右部连续位置。
如果结点度为1,则该结点只有左孩子,即不存在只有右子树的情况。
同样结点数的二叉树,完全二叉树的深度最小。
3、二叉树的性质
1、在二叉树的第i层上至多有2^(i-1)个结点。(i>=1)
2、深度为k的二叉树至多有2^(k-1)个结点。(k>=1)
3、对于任何一棵二叉树T,如果其叶结点数为n0,度为1的结点为n1,度为2的结点为n2,那么n0=n2+1。T的结点总数=n0+n1+n2。
4、具有n个结点的完全二叉树的深度为[log2(n)]+1。([x]表示不大于x的最大整数)。
5、如果对一棵有n个结点的完全二叉树(其深度为[log2(n)]+1)的结点按层序编号(从第1层到第[log2(n)]+1层,每层从左到右,对任一结点i(1<=i<=n)有:
(1)如果i=1.则结点i是二叉树的根,无双亲;如果i>1,则其双亲是结点[i/2]。
(2)如果2i>n,则结点i无左孩子(结点i为叶结点);否则其左孩子是结点2i。
(3)如果2i+1>n,则结点i无右孩子;否则其右孩子是结点2i+1。
上述性质自己画一个二叉树都是可以验证出来的。我们需要的是熟悉和理解性的记忆。
二叉树的遍历
遍历的方法有很多,如果限制了从左到右的习惯方式,那么主要有四种:
前序遍历:若二叉树为空则空操作返回,否则先访问根结点,然后前序遍历左子树,再前序遍历右子树。
中序遍历:若二叉树为空则空操作返回,否则从根结点开始,中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树。
后序遍历:若二叉树为空则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后访问根结点。
层序遍历(宽度优先遍历)
注意:在各个遍历过程中,注意递归的使用!!只有递归完成返回后,才能进行下一步,这种情况在后边的推导过程中很重要!!
前序遍历递归算法:
中序遍历递归算法:
后序遍历递归算法:
这样我们就可以得出二叉树遍历的两个性质:
1、已知前序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
2、已知后序遍历序列和中序遍历序列,可以唯一确定一棵二叉树。
但是已知前序遍历序列和后序遍历序列,是不能确定一棵二叉树的。
1、重建二叉树:(即二叉树的推导)
题目:已知一棵二叉树的前序遍历序列ABCDEF,中序遍历序列CBAEDF,请问这个二叉树的后续遍历序列?
解答:前序遍历肯定先遍历根结点,那么这个二叉树的根结点是A,在看中序列A的位置,我们可以大概的分出来CB和EDF分别根结点A的两个子树。
再看前序遍历序列里面,A-B-C,根据前序遍历序列的规则:前序遍历左子树,再前序遍历右子树,我们可以确定B是A的左孩子,C只能是B的孩子,再看中序遍历序列里面CBA的顺序,我们知道了C是B的左孩子,如果C是B的右孩子,那么中序遍历序列打印结果就是BCA...了。
前序遍历序列中DEF,那么D是A的右孩子,中序遍历序列中EDF,说明E是D的左孩子,F是D的右孩子。所以我们的二叉树就出来了,那么后序遍历序列的结果就是:CBEFDA。
我们的推导思路是这样的,但是写成代码是什么样呢,因为我们在开发过程中,不可能只是告诉电脑思路是什么样的,必须用代码的形式告诉电脑,然后电脑才能执行。
二叉树结点的定义如下:
struct BinaryTreeNode{
int m_nValue;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
}
这个过程好繁琐,具体的注释就不写了,,,因为我也只是简单理解了思路。。。
2、二叉树的深度
通过这个题目,我们引申出来“平衡二叉树”的概念。
题目一:输入一棵二叉树的根结点,求该树的深度。从根结点到叶结点依次经过的结点形成树的一条路径,最长路径的长度为树的深度。
题目二:输入一棵二叉树的根结点,判断该树是不是平衡二叉树。如果某二叉树中任意结点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
当然还有更简单遍历一次的方法,参考剑指offer210页。
关于二叉树的题目有很多,例如上边我们提到的重建二叉树和二叉树的深度。还有二叉树的子结构、二叉树的镜像、二叉搜索树的后续遍历序列、二叉树和双向链表、二叉树的下一个结点、对称的二叉树、把二叉树打印成多行、按之字顺序打印二叉树、序列化二叉树、二叉搜索树的第k个结点等等。。。这里我们不一一赘述了。
参考资料:《大话数据结构》作者:程杰。清华大学出版社。
《剑指offer》作者:何海涛。电子工业出版社。
最后,哪里不对的地方可以给我留言,我会及时改进的,谢谢大家。