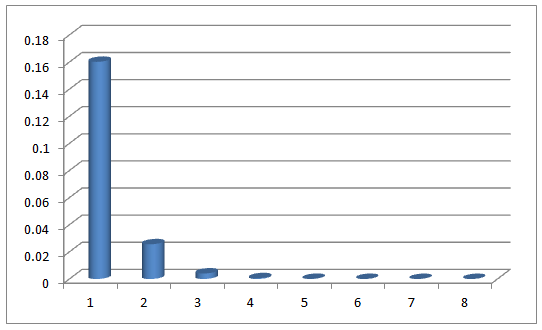
现在我们做一个实验,我们将同一枚硬币连续抛两次,恰好这两次都出现正面的概率是多少?
独立事件就是指事件B发生或者不发生都不会对事件A产生影响,然后我们就可以说事件A与事件B之间存在某种独立性。
2017年大乐透一共发行啦153期。我们来看看第一期跟第二期之间的关系。
第一期的开奖日期是1月2日,第二期的开奖日期是1月4日,这两个开奖日期是不同的日期,相互之间的开奖结果也不存在影响,所以说这两次开奖事件是相互独立事件。
大乐透的每一次的开奖事件都是一件独立事件。
一:
现在我们提第一个问题,根据我们的根果图,2017年大乐透第一期4奇1偶的出现概率是0.1602,那么第二期出现4奇1偶的概率是多少?
其实还是0.1602,因为两次开奖事件是相互独立事件,第一期的开奖结果并不影响到第二期。就像是抛硬币一样,连续抛两次同一枚硬币,第一次正面向上的概率是1/2,第二次正面向上的概率还是1/2。
二:
现在我们提第二个问题,根据我们的根果图,2017年大乐透第一期4奇1偶的出现概率是0.1602,那么连续两期出现4奇1偶的概率是多少?
相对比于第一个问题,就多啦两个字,连续。再次对比于抛硬币试验,连续抛两次同一枚硬币,恰好这两次都是正面向上的概率是1/2 x 1/2 = 1/4。跟这个问题类似,连续两期出现4奇1偶的概率是:
0.1602 x 0.1602=0.02566404。
0.02566404是小于0.1602的,那么为什么让0.1602乘以0.1602呢 ?这里涉及到一个问题,在数学上称为n次独立重复试验的问题,又被称为n重伯努利试验。
伯努利试验是在同样的条件下重复的,相互独立的进行的一种随机试验,其特点是该随机试验只有两种可能结果:发生或者不发生。即结果只有成功或者失败。我们假设该项试验独立重复地进行啦n次,那么就称这一系列重复独立的随机试验为n重伯努利试验,也被称为伯努利概型。如果一件事情只重复1次,我们研究伯努利试验就没有任何意义,但是当我们反复的进行伯努利试验的时候,事情就变得有意义啦,数据一旦累积下来就会有很多有用的信息展示出来,我们可以去分析借鉴。
大乐透里连续两期开出4奇1偶的概率就满足n重伯努利试验,首先伯努利试验是在同样的条件下重复的,相互独立的进行的一种随机试验。而大乐透的每期的开奖也是在同样的条件下重复的,并且相互独立的进行的一种随机试验,而每期要不能开出4奇1偶,要不就是不能开出4奇1偶,即试验的结果只有两种:发生或者不发生。所以说大乐透里连续两期开出4奇1偶这样一种随机试验是伯努利试验。
n重伯努利试验的定理是:设在一次试验中,事件A发生的概率是p,则在n重伯努利试验中,事件A恰好发生k次的概率为:
我们发现大乐透开出1期4奇1偶的概率是0.1602,那么连续开出2期的概率是0.02566404,也就是开出1期4奇1偶容易,但是连续两期开出2期4奇1偶的话就比较困难 ,只有0.02566的概率,对比一下0.1602和0.02566404,0.1602/0.02566404 =6.2倍。多啦两个字“连续”,难度往上提高啦6倍。
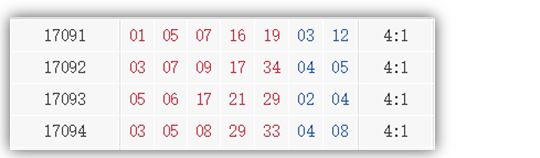
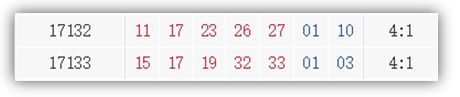
我们来统计一下历史数据,看看大乐透2017年的开奖结果,看看在2017年中,大乐透前区连续两期开出啦4奇1偶的情况。
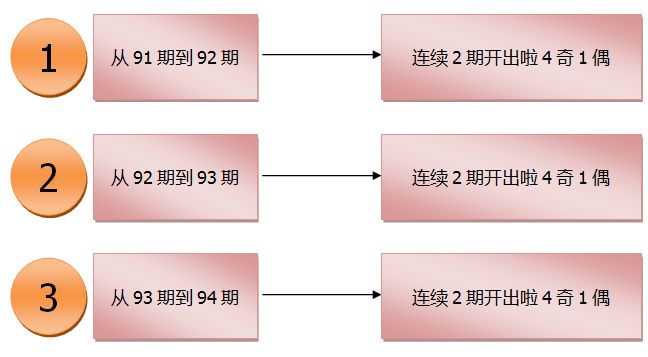
2017年从第91期开始一直到94期,连着4期开出啦4奇1偶,其实我们可以把这种情况拆分一下。
我们研究的课题是连续两期开出4奇1偶的概率,而在2017年连着4期开出啦4奇1偶的情况,所以我们这里可以把这种情况按照我们“连续2期”的逻辑来划分一下这4期,总共划分出来3种情况,而且这3种情况都是不同的种类。
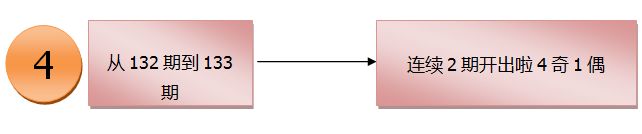
在2017年,像这样连续2期开出4奇1偶的情况,一共发生啦4次。大乐透一年开154期,像这样的情况一共发生啦4次,说明这样的情况不具有普适性。那为什么偏偏是4次,而不是20次,30次呢,在这个4次的背后又隐藏着什么样的学问呢?下面我们来探索一下走势图上的4次背后的深刻的原因。
可以设想这么一个情景:一个人,一扇纸窗户,一朵花。
我们是这样来看待彩票的,一个人站在一扇纸窗户的前面,纸窗户的后面有一朵花,这个人隔着这扇窗户来看窗户后面的花,看的不太清楚,隐隐约约的只能看到一点花的模样。但是他很清楚,这一扇纸窗户后面是有一朵花的,他相信自己的眼睛,他相信自己所看到的。
捅不破的纸窗户。
这一段话,基本上就代表着我们目前的彩票水平。那一朵花就代表着彩票,有很多老彩民都是知道彩票里面是有规律的,但是却像隔着纸窗户看花一样,看的不是太清楚。而纸窗户代表的就是彩票里面的规律,要想捅破这一层窗户纸看清楚这一朵花很简单,也很难。通过学习《西瓜经》的上卷《现在经》,其实我们已经将这一层窗户纸捅破啦,但是我们的灵魂还没有升级到可以预测的境界,我们只是看懂啦一些彩票里面的坑坑洼洼,比如知道啦5连号是最好不要购买的,大约知道啦我们所面对的是一个什么样的彩票世界。
从现在的角度去看待彩票,还隔着一层窗户纸,看的不是太清楚。那从未来的角度去看待彩票,彩票更是一团迷雾,看都看不见。确实如此,一个人在厉害,你还能算的出来明天的号码不成。这个很难。
简单的隔壁就是困难。其实未来比现在也就多啦一层窗户纸。要想看见彩票的未来趋势,只需要捅破两层窗户纸就可以啦。一层窗户纸我们已经捅破啦,两层窗户纸要想捅破它很难吗?当然很简单,只需要轻轻一下就可以啦。最难的地方不是难在捅破它,而是你要发现它是一层窗户纸,知道窗户纸的物理特性。
要想掌握彩票预测学,必须的学会如何去捅破两层窗户纸,必须的掌握n次独立重复试验。
我们知道大乐透4奇1偶每一期的开出概率是0.1602,比如17年的第一期,那这一期4奇1偶的开出概率就是0.1602,我们可以把第一期4奇1偶的开出概率比喻成一层窗户纸。那第二期4奇1偶的开出概率依然还是0.1602,我们还可以把这一期4奇1偶的开出概率比喻成一层窗户纸。这样目前我们就看到
啦2层窗户纸。那我们现在提出一个问题:
假如2017年大乐透第一期开出啦4奇1偶,紧接着第二期还是开出啦4奇1偶,第三期明天开奖。假如我们今天要写号投注,那么请问第三期也就是明天的号,你是否要还是要选择4奇1偶进行投注?
其实第三期接着选择4奇1偶进行投注不明智。这是因为根据n次独立重复试验,大乐透连续3期4奇1偶的开出概率仅仅为:
0.1602 x 0.1602 x 0.1602 =0.00411137。也就是千分之四的概率,也就是说假如你明天还是要选择4奇1偶进行投注,那么你的中奖概率是千分之四。那这个概率就有点低啦。所以不建议投注。
现在我们再提一个问题:
还是假如2017年大乐透第一期开出啦4奇1偶,紧接着第二期还是开出啦4奇1偶,无巧不成书,第三期依然还是开出啦4奇1偶,第四期明天开奖。假如我们今天要写号投注,那么请问第四期也就是明天的号,你是否依然要选择4奇1偶进行投注?
有的彩民很倔的,做事就喜欢走偏门,第四期的投注号,你依然还是选择啦4奇1偶进行投注,那么你的上岸概率是多少?
0.1602 x 0.1602 x 0.1602 x 0.1602
=0.0006586。万分之六的概率。
千分之四等于万分之四十。连续三期开出4奇1偶的概率是万分之四十,连续四期开出4奇1偶的概率却是万分之六,很显然万分之六更低。万分之六约等于1/ 1666。也就是说你上岸的概率是1/16666。
那假如第四期你要是不选择4奇1偶进行投注,转而选择3奇2偶进行投注,那么你上岸的概率是有多少呢?我们知道3奇2偶每一期的开出概率是0.3418,因为上一期并没有开出3奇2偶,所以说连续1期开出3奇2偶的概率还是0.3418,所以说你上岸的概率是0.3418,也就是说是34/100,大约等于1/3,对比1/3和1/1666,很明显选择1/3要明智的多。
现在我们再提最后一个问题:
还是假如2017年大乐透第一期开出啦4奇1偶,紧接着第二期还是开出啦4奇1偶,无巧不成书,第三期依然还是开出啦4奇1偶,更让人惊奇的是,第四期还是开出啦4奇1偶,第五期明天开奖。假如我们今天要写号投注,那么请问第五期也就是明天的号,你是否依然要选择4奇1偶进行投注?
有的彩民可能这个时候,就会自己去算啦。
0.1602 x 0.1602 x 0.1602 x 0.1602 x 0.1602
=0.0001055。万分之一的上岸概率。
我们发现啦这样一个规律,就是在n重独立重复试验中,一件事连续开出的概率越是开出的次数越多,那么它开出的概率就会相应的呈现递减的趋势,这是因为从根本上说随机事件的概率发生值位于0到1之间,也就是说正是因为小于1,所以它才会越乘越小,要是大于1,那就会越乘越大。如果要是越乘越小,小到极限的时候就是0。
其实当0.1602连续开到5次方的时候,概率小的就可以忽略不计啦。
越开越小,越是连乘的次数越多,开出的概率越小,直到n的次数趋向于无穷大,开出的概率就变成0。