2017CVPR--Adversarial Discriminative Domain Adaptation 对抗判别域适应
ADDA是当前域适应方法中较为出色的一种,同时也是一种典型的asymmetric transformation。看了一些关于该论文的笔记,觉得不够通俗,于是自己总结了一下,也希望可以帮助大家稍微理解一点。
论文地址:https://arxiv.org/abs/1702.05464
背景
生成对抗学习是现今一种很具前景的方法,生成器通过将源域分布不断的更新改进,使源域分布近似于目标域分布甚至是等同于目标分布,从而让域判别器无法识别出数据是来自哪一域。域适应是迁移学习的一部分,迁移学习则是想利用类似于目标分布的源分布,从中迁移出对目标任务分类有益的“知识”,或者是将源分布与目标分布映射到“共同特征空间”,完成对目标任务的无监督/半监督/少样本学习等。对抗学习与迁移学习的融合是当前迁移学习领域中的一个热点,一些方法通过将对抗学习用于无监督域适应,确实减少了源域和目标域之间的差异,并提高了泛化能力,但是其中也存在一些改进的地方,比如CoGAN对源域和目标域之间不太相似的情况下表现的不太满意、使用梯度反转在判别器训练前期会收敛的很快,但会导致梯度的逐渐消失、使用权值共享的对称映射(Symmetric mapping)使得源分类器表现很棒,但是在多源域的情况下表现就不好。因此提出了一个简易而有效的ADDA框架,并在MNIST, USPS, 和 SVHN数据集上超越了当时的state-of-the-art效果。
解决思路
作者认为之前不同的算法主要不同于设计:1.是否使用生成或者是判别基础模型 2.使用何种损失函数(优化) 3.是否在域间分享权值(源域和目标域映射)。 如下图:
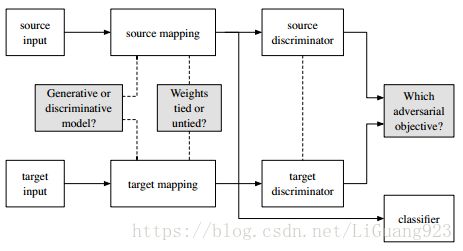
而作者也从这几个部分详细的介绍了ADDA。
一、源域和目标域映射
如何最小化源域和目标域映射的距离是一个开放的问题,因此,第一步是将这些映射参数化。无监督域适应通常认为目标判别任务是一些分类任务,以前的域适应方法一般是在域间建立域适应判别模型。通过一个判别基础模型,输入图像被映射到对判别任务(例如图像分类)有用的特征空间中,例如在数字识别中,可能是一个标准的LeNet模型。而对于将域适应和对抗模型相结合的例子,Liu和Tuzel使用了两个生成对抗网络完成MNIST到USPS的迁移,并取得了很好的效果,这些生成模型使用随机噪声作为输入以在图像空间中生成样本,然后,网络中的对抗判别器的中间特征被用来训练一个目标任务分类器。这些特征空间啊,中间特征啊,就是对源域的映射结果,而完成这些映射的参数即映射的参数化。
一旦确定了源域的映射参数化 M s M_s Ms,我们就必须决定如何参数化目标映射 M t M_t Mt。通常,目标映射几乎总是在特定功能层(架构)方面与源域匹配(比如模型中的某些结构类似、将模型间的参数绑定),但是不同的方法已经提出了各种正则化技术。所有的方法都使用源映射来初始化目标映射参数,但是不同的方法在目标域和源域映射之间使用了不同的约束条件,即 ψ ( M s , M t ) \psi(M_s,M_t) ψ(Ms,Mt),而目的是通过约束源域映射和目标映射,来完成最小化源域和目标域之间的距离。
而常用的一种约束是源域和目标域之间的层级相等:
ψ ι i ( M s ι i , M t ι i ) = ( M s ι i = M t ι i ) \psi_{\iota_i}(M_s^{\iota_i},M_t^{\iota_i})=(M_s^{\iota_i}=M_t^{\iota_i}) ψιi(Msιi,Mtιi)=(Msιi=Mtιi)
这些相等约束可以在卷积网络框架中通过权值共享很容易实现。通过限制所有的网络层,这样可以强制源域和目标域映射保持一致,学习这样的对称转换(symmetric transformation)可以节省模型中的参数(因为目标映射和源域映射参数基本一致)。然而因为这种约束比较粗鲁,通常使得优化条件较差,失去了一些特定域特征,这导致了在使用一个网络处理来自两个不同域的图片的情况下表现不太理想。
而另一种方法则是学习一种非对称性变换(asymmetric transformation):只对网络层中的某一部分加以限制,从而强制部分对齐。Rozantsev表示部分权值共享也可以产生有效的适应性。
二、损失函数选择(Adversarial losses对抗损失)
当目标映射参数化确定以后,就可以使用对抗损失来学习实际映射了。存在很多种不同的对抗损失函数可以选择,而每种损失函数都有他们自己独特的使用场景。所有的对抗损失都使用一种标准的分类损失$\mathcal{L}_{adv_D} $来训练对抗判别器:
L a d v D ( X s , X t , M s , M t ) = − E x s ∼ X s [ l o g D ( M s ( x s ) ) ] − E x t ∼ X t [ l o g ( 1 − D ( M t ( x t ) ) ) ] \mathcal{L}_{adv_D} (X_s,X_t,M_s,M_t) = -E_{x_s\sim X_s}[logD(M_s(x_s))]-E_{x_t\sim X_t}[log(1-D(M_t(x_t)))] LadvD(Xs,Xt,Ms,Mt)=−Exs∼Xs[logD(Ms(xs))]−Ext∼Xt[log(1−D(Mt(xt)))]
然后,不同的是在训练映射中使用的损失函数 L a d v M \mathcal{L}_{adv_M} LadvM,《Domainadversarial training of neural networks》中梯度反转层中直接使用最大最小化判别器损失来优化映射:
L a d v M = − L a d v D \mathcal{L}_{adv_M} = -\mathcal{L}_{adv_D} LadvM=−LadvD
而直接进行梯度反转是有问题的,因为在训练判别器早期收敛的较快,从而导致了梯度消失。将该式子分为两个独立的式子,一个用于生成器,一个用于判别器,其中 L a d v D \mathcal{L}_{adv_D} LadvD保持不变,而 L a d v M \mathcal{L}_{adv_M} LadvM变为:
L a d v M ( X s , X t , D ) = − E x t ∼ X t [ l o g ( D ( M t ( x t ) ) ) ] \mathcal{L}_{adv_M} (X_s,X_t,D) = -E_{x_t\sim X_t}[log(D(M_t(x_t)))] LadvM(Xs,Xt,D)=−Ext∼Xt[log(D(Mt(xt)))]
这样与minimax损失有着相同的固定点属性,但是为目标映射提供了更强的梯度。称这种经过修改的损失函数为"GAN loss function"。到此,已经为源域和目标域使用了独立的映射,并且只对抗的学习了 M t M_t Mt( M s M_s Ms被固定)。这与GAN的设置是类似的,其中真实图像分布保持固定,生成分布通过学习以匹配它。GAN损失函数是生成器模拟另一个不变分布的标准选择。
三、ADDA
在上述的三个选择:是否选择生成或判别基础模型,是否权值共享,使用何种对抗损失函数,ADDA使用了一个判别基础模型,权值不共享和标准的GAN损失。框架流程如下图所示:
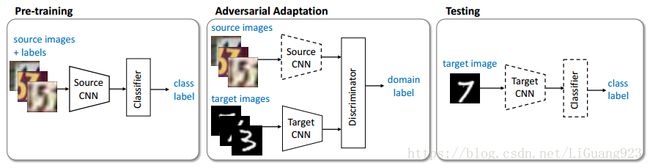
首先,作者选择了一个判别基础模型,因为假设生成令人信服的域内样本所需的大部分参数与判别适应任务无关。大多数之前的对抗适应性方法也因为这个原因直接在判别空间中优化。
接下来,将源域和目标域映射通过解开权值完成独立。这是一种更具有灵活性的学习方式,因为它允许更多的域特定特征被提取出来用以学习。由于目标域是没有标签可用的,因此,没有权值共享,如果不注意正确的初始化和训练程序,目标模型有可能会导致学习退化的现象。可以这么理解,如果源和目标没有约束,根据对抗损失各自学习的话,很有可能会产生类似于震荡效果的学习,即学习的退化,也不容易找到最优点,因此,在ADDA中,对网络增加了一个约束,这个约束就是对源模型进行预训练(图中的第一个),并且在对抗适应性中固定源模型参数(图中的第二个)来完成,这样可以将源模型作为一个参照,通过损失梯度传递,将经过映射的目标域数据分布逐渐逼近源映射后的数据分布,以至于判别器无法区分源域和目标域。
通过这样做,可以有效的学习到一个非对称映射,其中,通过修改目标模型以致于匹配源分布。这与原始的生成对抗学习设计很相似,其中生成空间被更新直到判别器无法分辨。因此,也选择了GAN损失函数。ADDA对应的无限制优化如下:
min M s , C L c l s ( X s , Y s ) = − E ( x s , y s ) ∼ ( X s , Y s ) ∑ k = 1 K 1 [ k = y s ] l o g C ( M s ( x s ) ) \mathop{\min}\limits_{M_s,C} \mathcal{L}_{cls}(X_s,Y_s)= -E_{(x_s,y_s)\sim (X_s,Y_s)} \sum_{k=1}^{K} 1_{[k=y_s]} log C(M_s(x_s)) Ms,CminLcls(Xs,Ys)=−E(xs,ys)∼(Xs,Ys)k=1∑K1[k=ys]logC(Ms(xs))
min D L a d v D ( X s , X t , M s , M t ) = − E x s ∼ X s [ l o g D ( M s ( x s ) ) ] − E x t ∼ X t [ l o g ( 1 − D ( M t ( x t ) ) ) ] \mathop{\min}\limits_{D} \mathcal{L}_{adv_D}(X_s,X_t,M_s,M_t)= -E_{x_s\sim X_s} [log D(M_s(x_s))]- E_{x_t\sim X_t} [log(1- D(M_t(x_t)))] DminLadvD(Xs,Xt,Ms,Mt)=−Exs∼Xs[logD(Ms(xs))]−Ext∼Xt[log(1−D(Mt(xt)))]
min M s , M t L c l s ( X s , X t , D ) = − E x t ∼ X t [ l o g D ( M t ( x t ) ) ] \mathop{\min}\limits_{M_s,M_t} \mathcal{L}_{cls}(X_s,X_t,D)= -E_{x_t\sim X_t} [log D(M_t(x_t))] Ms,MtminLcls(Xs,Xt,D)=−Ext∼Xt[logD(Mt(xt))]
以上的损失函数很好理解,第一个式子中, C ( M s ( x s ) ) C(M_s(x_s)) C(Ms(xs))是第一幅图中Source CNN的输出,根据网络输出和标签计算损失。第二个式子则是计算第二幅图中判别器中的损失,就是将被固定的Source CNN输出 M s ( x s ) M_s(x_s) Ms(xs)和Target CNN的输出 M t ( x t ) M_t(x_t) Mt(xt)在经过判别器D的输出后的加权,相当于将判别器判别输出是来自源CNN的还是来自目标CNN的权重进行相加。第三个式子则是求域适应后的目标CNN的预测损失。
实验
实验部分不详细展开了,无非就是通过数据集与各种方法比较,最终还是自己的方法表现最好,感兴趣的同学可以看论文中的实验部分。
总结
ADDA框架主要从三个部分设计:基础模型(ADDA为判别基础模型),是否权值共享(层级约束,ADDA选择不添加层级约束),使用何种损失函数来确保映射(ADDA选择使用GAN loss),其中是否权值共享是关键,ADDA中选择不进行权值共享,因为一些域特异特征对最终分类器也可能会有较大帮助,因为这一点,可以看出ADDA的域适应思想是基于固定源域映射,而使目标映射靠近源映射,靠近的过程则是通过损失函数优化完成,通过这样完成域适应,从而将优化后的目标模型用于目标数据中的无监督学习。而现今另一种思路:通过权值分享(参数绑定)进行域适应,则是希望将源域和目标域进行共同的映射,映射到所谓的latent feature space,而所做的优化则是优化这种共同的映射,使得latent space更为合理,同时使得源和目标的差异更小,完成域适应。
参考文献
- Tzeng E, Hoffman J, Saenko K, et al. Adversarial Discriminative Domain Adaptation[J]. 2017.