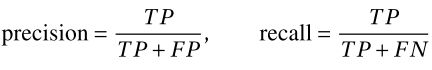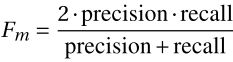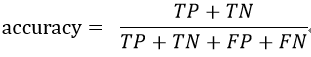用简单的例子来理解机器学习中的precision、recall、F1-score、accuracy
主要介绍机器学习中的precision、recall、F1-score、accuracy的计算方法,以及为什么在有些情况下要用F1-score而不是precision来衡量机器学习分类效果。
通常来说,在机器学习分类项目中,我们一般:
用precision来评估某类别分类的准确性;
用accuracy来评估总体分类的准确性。
但对于一些数据数量占比不平衡的数据集来说,计算分类的准确性就不能单单依靠precision和accuracy,
还要考虑recall和F1-score。
在文献中经常用以下算式来定义他们,
其中TP=True Positive,TN=True Negative,FP=False Positive,FN=False Negative
这是因为把它假设成为了一种含有两个标签的分类问题(个人猜测源于医学检查中的真阳性、真阴性、假阳性、假阴性):
标签有Positive和Negative(你也可以写成下面例子中的cat与not cat(dog))。
True和False则表示预测的对不对。
比如现在有一个数据集,其中有{cat:5, dog:100},可以看出两种类别数量严重失衡。
经过机器学习模型分类后,生成了如下混淆矩阵:
| cat | dog | |
| cat | 4 | 1 |
| dog | 20 | 80 |
(1)对于cat来说:
| cat | not cat | |
| cat | 4(TP) | 1(FP) |
| not cat | 20(FN) | 80(TN) |
precision=TP/(TP+FP)= 4/(4+1) = 4/5 = 0.80
precision=预测为cat实际为cat数量 /(预测为cat实际为cat数量+预测不是cat实际为cat数量=cat的总数)
recall=TP/(TP+FN)= 4/(4+20)= 0.167
recall=预测为cat实际为cat数量 /(预测为cat实际为cat数量+预测为cat实际不是cat数量)
Fm=2*precision*recall/(precision+recall) =2*0.8*0.167 / (0.8+0.167) = 0.276
accuracy=(TP+TN)/(TP+TN+FP+TN) = (4+80) / (4+80+1+20) = 0.8
(2)对于dog来说:
| dog | not dog | |
| dog | 80(TP) | 20(FP) |
| not dog | 1(FN) | 4(TN) |
precision=TP/(TP+FP) = 80/(80+20) = 80/100 = 0.80
precision=预测为dog实际为dog数量 /(预测为dog实际为dog数量+预测不是dog实际为dog数量=dog的总数)
recall=TP/(TP+FN) = 80/(80+1) = 0.988
recall=预测为dog实际为dog数量 /(预测为dog实际为dog数量+预测为dog实际不是dog数量)
Fm=2*precision*recall/(precision+recall) =2*0.8*0.988/ (0.8+0.988) = 0.884
accuracy=(TP+TN)/(TP+TN+FP+TN) = (80+4) / (80+4+20+1) = 0.8
我们可以发现,对于cat和dog,precision都是0.8,但他们的recall和F1-score是不一样的,dog的F1-score比cat高很多。
这与我们直观理解是相符的,(从100个数据中分辨对80个数据)通常比(从5个数据中分辨对4个数据)可靠度高。
用统计学理论来证明这点:
假设对cat的单词预测准确率为p,对dog的单次预测准确率为q,
那么对于{cat:5, dog:100},使得对cat和dog的总预测准确率都要达到80%,
即![]()
若使上式要成立,则q > p。
即对于{cat:5, dog:100}来说,对cat和dog的总预测准确率都达到80%时,对dog的单次预测准确率q是要大于对cat的单次预测准确率p的。
对于多分类问题也是相同的,比如{cat:5, dog:100, bird:10}
分类生成的混淆矩阵(别在意为什么有bird被认为成了cat,有可能是只owl)
| cat | dog | bird | |
| cat | 4 | 1 | 0 |
| dog | 20 | 80 | 0 |
| bird | 1 | 0 | 9 |
那么对cat来说:
| cat | not cat | |
| cat | 4(TP) | 1(FP) |
| not cat | 21(FN) | 89(TN) |
precision=TP/(TP+FP)= 4/(4+1) = 4/5 = 0.80
precision=预测为cat实际为cat数量 /(预测为cat实际为cat数量+预测不是cat实际为cat数量=cat的总数)
recall=TP/(TP+FN)= 4/(4+21)= 0.160
recall=预测为cat实际为cat数量 /(预测为cat实际为cat数量+预测为cat实际不是cat数量)
Fm=2*precision*recall/(precision+recall) =2*0.8*0.160 / (0.8+0.160) = 0.267
accuracy=(TP+TN)/(TP+TN+FP+TN) = (4+89) / (4+89+1+21) = 0.807