机器学习（1）——概率图模型之隐马尔科夫模型

1、概念

在概率模型( probabilistic model )中，利用已知变量 “推断( inference )” 未知变量的条件分布。

假定未知变量为 $Y$ ，已知变量为 $X$ ，其他变量为 $R$，生成式模型考虑联合分布$P(Y,R,X)$,判别式模型考虑条件分布$P(Y,R|X)$ 。推断就是根据$P(Y,R,X$ 或 $P(Y,R|X)$ 得到条件概率分布 $P(Y|X)$ 。

概率图模型( probabilistic graphical model ) 是一类用图表达变量相关关系的概率模型。一个节点表示一个或一组随机变量，节点之间的边表示变量间的概率相关关系。根据边的性质不同，概率图模型可以分为两种：第一类使用有向无环图表示变量之间的依赖关系，称为有向图模型或贝叶斯网( Bayesian network )；第二类是使用无向图表示变量之间的相关关系，成为无向图模型或马尔可夫网( Markov network )。

这里依赖关系是指函数关系，当一个或几个变量取一定值时，另一个变量有确定值与之对应。当变量X取某个值时，变量Y的取值可能有若干个，这些数值表现为一定的波动性，但总是围绕着它们的平均数，并遵循一定的规律变动。变量之间存在的这种不确定的数量关系称为相关关系。特点：Y与X的值不一一对应；Y与X的关系不能用函数式严格表达，但有规律可循。

区分相关关系与函数关系的依据全凭因变量取值的确定性：若因变量的取值是确定的、唯一的，则两个变量之间的关系称为函数关系；若因变量的取值是不确定的，则两个变量之间的关系称为相关关系。

2、隐马尔科夫模型

隐马尔科夫模型（HMM）是结构最简单的动态贝叶斯网，是一种著名的有向图模型。

马尔可夫链（Markov chain）：系统下一时刻的状态仅由当前状态决定，不依赖于以往的任何状态。

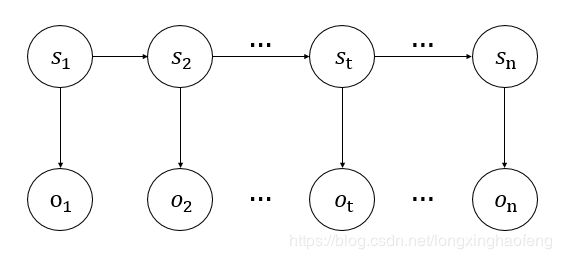
隐马尔科夫模型中，状态变量可分为两组。第一组为隐藏的状态变量 $y_t\in \left\{s_1,s_2,\cdots ,s_N\right\}$ ，$y_t$ 表示 $t$ 时刻的状态，共 $N$ 个状态，此状态变量为未知变量（也称为隐变量） $S$ 。第二组为可观测的状态变量，$x_t=\left\{o_1,o_2,\cdots ,o_M\right\}$ ,$x_t$ 表示 $t$ 时刻的观测状态，此状态变量为已知变量 $O$ 。

2.1、《机器学习》（周志华著）中的例子

观测值 $x_t\in O$ 由 $y_t\in S$ 决定，状态值 $y_t$ 由 $y_{t-1}$ 决定, $t$ 为时刻。箭头所指方向为状态可转变的方向（依赖关系）。

所有变量的联合概率分布如下：
$$P(x_1,y_1,\cdots ,x_n,y_n)=P(y_1)P(x_1|y_1)\prod _{t=2}^{n}P(y_t|y_{t-1})P(x_t|y_t)$$
在等式1中，$P(x_t|x_1,y_1,\cdots ,x_{t-1},y_{t-1},y_t)=P(x_t|y_t)$ , $x_t$ 与其他变量无关，仅与 $y_t$ 有关。这里涉及马尔可夫模型的另一个假设，独立性假设：假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其它观测状态无关。欲求 $x_t$ ,只能先求与其相关的 $y_t$ 。
$$P(x_t|y_1,\cdots ,y_t,x_1,\cdots ,x_{t-1})=P(x_t|y_t)$$
所以可以将 $(x_t,y_t)$ 看作一组变量 $s_t$，其联合概率分布为 $P(s_t)=P(y_t|y_{t-1})P(x_t|y_t)$ 。

所有 $s$ 变量的联合概率分布如下：
$$P(s_1,s_2,\cdots ,s_t,s_n)=P(s_1)\prod _{t=2}^{n}P(s_t)$$

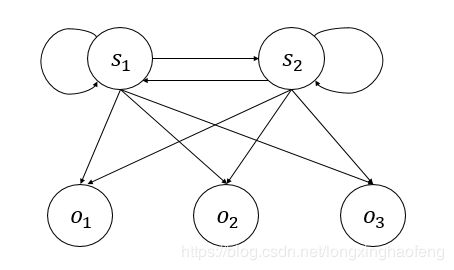
2.2、更为一般的HMM模型

隐藏的状态变量 $S=\left\{s_1,s_2\right\}{y}_t\in S$ ，可观测的状态变量 $O=\left\{o_1,o_2,o_3\right\}{x}_t\in O$ ,箭头所指方向为状态可转变的方向（依赖关系）。

观测值 $x_t$ 由 $y_t$ 决定，状态值 $y_t$ 仅由 $y_{t-1}$ 决定（这里再强调一遍）。

马尔可夫概率公式如下：
$$P(s_1,s_2,\cdots ,s_n)=P(s_1,s_2,\cdots ,s_{n-1})P(s_n|s_1,s_2,\cdots ,s_{n-1})$$
此处的 $s$ 与等式3中的 $s$ 不同，仅将其当作一个状态变量，包含隐藏状态变量和观测状态变量。等式3求所有变量的联合概率分布，即所有变量状态同时存在的概率。等式4求某一状态基于其他状态存在的概率，这一状态可以是隐藏状态，也可以是观测状态。等式3、4本质相同。

若可观测状态序列为 $\left\{o_1,o_2,o_3\right\}$ ,其 $P(O)$ 概率为：

$t=1$ 时，观测状态为 $x_1=o_1$ 的概率：
$$P(o_1,y_1)=P(y_1)P(o_1|y_1)$$
如果 $y_1=s_1$：
$$P(o_1,s_1)=p(s_1)P(o_1|s_1)$$
如果 $y_1=s_2$：
$$P(o_1,s_2)=p(s_2)P(o_1|s_2)$$
$t=2$ 时，观测状态为 $x_2=o_2$ 的概率：

$$\begin{array}{rl}P(o_1,o_2,y_2)& =P(o_1,o_2,y_1,y_2)\\ & =P(o_1,y_1)P(y_2|y_1)P(o_2|y_2)\end{array}$$

如果 $y_2=s_1$：
$$P(o_1,o_2,s_1)=P(o_1,s_1)P(s_1|s_1)P(o_2|s_1)+P(o_1,s_2)P(s_1|s_2)P(o_2|s_1)$$
如果 $y_2=s_2$ ：
$$P(o_1,o_2,s_2)=P(o_1,s_1)P(s_2|s_1)P(o_2|s_2)+P(o_1,s_2)P(s_2|s_2)P(o_2|s_2)$$
$t=3$ 时，观测状态为 $x_3=o_3$ 的概率：
$$\begin{array}{rl}P(o_1,o_2,o_3,y_3)& =P(o_1,o_2,o_3,y_1,y_2,y_3)\\ & =P(o_1,o_2,y_1,y_2)P(y_3|y_2)P(o_3|y_3)\end{array}$$
如果 $y_3=s_1$：
$$P(o_1,o_2,o_3,s_1)=P(o_1,o_2,y_2)P(s_1|s_1)P(o_3|s_1)+P(o_1,o_2,y_2)P(s_1|s_2)P(o_3|s_1)$$
如果 $y_3=s_2$：
$$P(o_1,o_2,o_3,s_2)=P(o_1,o_2,y_2)P(s_2|s_1)P(o_3|s_2)+P(o_1,o_2,y_2)P(s_2|s_2)P(o_3|s_2)$$
等式16中 $P(o_1,o_2,y_2)$ 为 $t=2$ 时的概率，如等式9 。

综上：
$$P(o_1,o_2,o_3)=P(o_1,o_2,o_3,s_1)+P(o_1,o_2,o_3,s_2)$$

2.3、参数

一个隐马尔科夫模型包含三个参数 $\lambda =\left\{A,B,\Pi \right\}$ ,或将 $\lambda$ 表示为 $R$。

状态转移概率矩阵 $A=[a_{ij}{]}_{N\times N}$ ，表示模型在各个状态中转移的概率。
$$a_{ij}=P(y_{t+1}=s_j|y_t=s_i)1\le i,j\le N$$
表示在任意时刻 $t$ ，若状态为 $s_i$ ，则下一时刻状态为 $s_j$ 的概率。

在2.2中的例子，$N=2$
$$A=\left[\begin{array}{cc}0.1& 0.9\\ 0.8& 0.2\end{array}\right]$$
行向量表示 $t$ 时刻，纵向量表示 $t+1$ 时刻。横向量累加和为 $1$ 。

此矩阵表示隐藏状态，也就是 $S$ 之间专业的概率。

输出观测概率矩阵 $B=[b_{ij}{]}_{N\times M}$ ，表示模型根据当前状态获得各个观测值的概率。
$$b_{ij}=P(x_t=o_j|y_t=s_i)1\le i\le N,1\le j\le M$$
表示在任意时刻 $t$ ，若状态为 $s_i$ ，则观测值 $o_j$ 的概率。

在2.2中的例子，$N=2，M=3$
$$B=\left[\begin{array}{ccc}0.7& 0.1& 0.2\\ 0.3& 0.5& 0.2\end{array}\right]$$
行向量表示隐藏状态，纵向量表示观测状态。横向量累加和为 $1$ 。

初始状态概率矩阵$\pi =({\pi }_1,{\pi }_2,\cdots ,{\pi }_n)$ ，模型在初始时刻隐藏状态出现的概率。
$${\pi }_i=P(y_1=s_i)1\le i\le N$$
表示模型的初始状态为 $s_i$ 的概率。

在2.2中的例子，$N=2$
$$\Pi =\left[\begin{array}{cc}0.3& 0.9\end{array}\right]\Pi =\left[\begin{array}{cc}0.3& 0.7\end{array}\right]$$

3、参考

隐马尔可夫模型（一）
周志华《机器学习》