python机器学习案例系列教程——极大似然估计、EM算法

全栈工程师开发手册 （作者：栾鹏）

python数据挖掘系列教程

极大似然

极大似然（Maximum Likelihood）估计为用于已知模型的参数估计的统计学方法。

也就是求使得似然函数最大的代估参数的值。而似然函数就是如果参数已知则已出现样本出现的概率。

比如，我们想了解抛硬币是正面（head）的概率分布 θ θ ；那么可以通过最大似然估计方法求得。

θ^=argmaxxl(θ)=argmaxxθ8(1−θ)2 θ ^ = a r g m a x x l ( θ ) = a r g m a x x θ 8 ( 1 − θ ) 2

其中， l(θ) l ( θ ) 为观测变量序列的似然函数。

所以最大似然方法估计参数，就是先假设参数已知，然后用参数，求出样本出现的概率。如果是多个样本，就是多个样本的联合概率最大

求解使似然函数最大的代估参数，常规的做法就是对似然函数求导，求使导数为0的自变量的值，以及左右边界线的值。

例如

对 l(θ) l ( θ ) 求偏导

∂l(θ)∂θ=θ7(1−θ)(8−10θ)⇒θ^=0.8 ∂ l ( θ ) ∂ θ = θ 7 ( 1 − θ ) ( 8 − 10 θ ) ⇒ θ ^ = 0.8

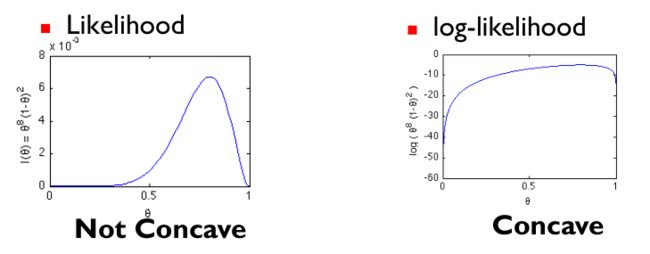
但是如果似然函数不是凹函数（concave），求解极大值困难。一般地，使用与之具有相同单调性的log-likelihood，如图所示也就是将似然函数求log。

所谓的凹函数和凸函数，凹函数斜率逐渐减小，凸函数斜率逐渐增大。所以凹函数“容易”求解极大值（极值为0时），凸函数“容易”求解极小值（极值为0时）。

EM算法

EM算法（Expectation Maximization）是在含有隐变量（latent variable）的模型下计算最大似然的一种算法。所谓隐变量，是指我们没有办法观测到的变量。比如，有两枚硬币A、B，每一次随机取一枚进行抛掷，我们只能观测到硬币的正面与反面，而不能观测到每一次取的硬币是否为A；则称每一次的选择抛掷硬币为隐变量。

用Y表示观测数据，Z表示隐变量；Y和Z连在一起称为完全数据( complete-data )，观测数据Y又称为不完全数据(incomplete-data)。观测数据的似然函数：

P(Y|θ)=∑zP(Z|θ)P(Y|Z,θ) P ( Y | θ ) = ∑ z P ( Z | θ ) P ( Y | Z , θ )

求模型参数的极大似然估计：

θ^=argmaxθlogP(Y|θ) θ ^ = a r g m a x θ l o g P ( Y | θ )

因为含有隐变量，此问题无法求解。因此，Dempster等人提出EM算法用于迭代求解近似解。

所以EM算法是一种特殊情况下的最大似然求解方法。

EM算法比较简单，分为两个步骤：

• E步（E-step），以当前参数 θ(i) θ ( i ) 计算 Z Z 的期望值。因为期望值中不再包含未知的隐含变量Z，所以是可以计算的。

Q(θ,θ(i))=EZ[logP(Y,X|θ)|Y,θ(i)] Q ( θ , θ ( i ) ) = E Z [ l o g P ( Y , X | θ ) | Y , θ ( i ) ]

• M步（M-step），求使 Q(θ,θ(i)) Q ( θ , θ ( i ) ) 极大化的 θ θ ，确定第 i+1 i + 1 次迭代的参数的估计值 θ(i+1) θ ( i + 1 )

θ(i+1)=argmaxθQ(θ,θ(i)) θ ( i + 1 ) = a r g m a x θ Q ( θ , θ ( i ) )

如此迭代直至算法收敛。

案例

如图所示，有两枚硬币A、B，每一个实验随机取一枚抛掷10次，共5个实验，我们可以观测到每一次所取的硬币，估计参数A、B为正面的概率 θ=(θA,θB) θ = ( θ A , θ B ) ，根据极大似然估计求解。

如果我们不能观测到每一次所取的硬币，只能用EM算法估计模型参数，算法流程如图所示：

隐变量 Z Z 为每次实验中选择A或B的概率，并初始化A为正面的概率为0.6，B为正面的概率为0.5。实验进行了5次。每次都要进行一遍EM操作。每次都要计算隐含变量。取A的概率，和取B的概率。然后更新代估参数 θA θ A （A为正面的概率）和 θB θ B （B为正面的概率）的值。

在初始化 θA=0.6 θ A = 0.6 和 θB=0.5 θ B = 0.5 后第一次实验后计算隐含变量（选择A的概率）为

P(z1=A|y1,θ0)=z1为A的话，样本结果出现的概率z1为任何可取值的话，样本结果出现的概率=P(z1=A|y1,θ0)P(z1=A|y1,θ0)+P(z1=B|y1,θ0)=0.65∗0.450.65∗0.45+0.510=0.45 P ( z 1 = A | y 1 , θ 0 ) = z 1 为 A 的 话 ， 样 本 结 果 出 现 的 概 率 z 1 为 任 何 可 取 值 的 话 ， 样 本 结 果 出 现 的 概 率 = P ( z 1 = A | y 1 , θ 0 ) P ( z 1 = A | y 1 , θ 0 ) + P ( z 1 = B | y 1 , θ 0 ) = 0.6 5 ∗ 0.4 5 0.6 5 ∗ 0.4 5 + 0.5 10 = 0.45

按照上面的计算方法可依次求出其他隐含变量 Z Z ，然后计算极大化的 θ(i) θ ( i ) 。经过10次迭代，最终收敛。

K均值聚类和EM算法

K均值聚类是无监督的聚类算法。
关于k均值聚类不了解的可以参考：https://blog.csdn.net/luanpeng825485697/article/details/78993977

k均值聚类的目的就是为了是下面的损失函数最小

J(c,u)=∑i=1m||xi−uci|| J ( c , u ) = ∑ i = 1 m | | x i − u c i | |

其中m为样本个数， xi x i 表示第 i i 个样本， ci c i 表示第第i个样本所属的聚类， uci u c i 表示第i个样本所属的聚类的质心。

假设当前 J J 没有达到最小值，那么首先可以固定每个类的质心 uj u j ，调整每个样例的所属的类别 cj c j 来让 J J 函数减少，同样，固定 cj c j ，调整每个类的质心 uj u j 也可以使 J J 减小。这两个过程就是内循环中使 J J 单调递减的过程。当 J J 递减到最小时， u u 和 c c 也同时收敛。

K-means与EM的关系

首先回到初始问题，我们目的是将样本分成K个类，其实说白了就是求一个样本的隐含类别y，然后利用隐含类别将x归类。由于我们事先不知道类别y，那么我们首先可以对每个样例假定一个y吧，但是怎么知道假定的对不对呢？怎样评价假定的好不好呢？

我们使用样本的极大似然估计来度量，这里就是x和y的联合分布P（x,y）了。如果找到的y能够使P(x,y)最大，那么我们找到的y就是样例x的最佳类别了，x顺手就聚类了。但是我们第一次指定的y不一定会让P(x,y)最大，而且P(x,y)还依赖于其他未知参数，当然在给定y的情况下，我们可以调整其他参数让P(x,y)最大。但是调整完参数后，我们发现有更好的y可以指定，那么我们重新指定y，然后再计算P(x,y)最大时的参数，反复迭代直至没有更好的y可以指定。

这个过程有几个难点：

第一怎么假定y？是每个样例硬指派一个y还是不同的y有不同的概率，概率如何度量。（kmean中是硬指定，距离哪个聚类近就属于哪个聚类）

第二如何估计 P(x,y) P ( x , y ) ， P(x,y) P ( x , y ) 还可能依赖很多其他参数，如何调整里面的参数让 P(x,y) P ( x , y ) 最大。（ J J 函数最小来代替 P(x,y) P ( x , y ) 最大，我们可以将这些参数写成 θ θ ，更简单的理解 θ θ 就是k个质心的选择）

按照EM算法思想: E步就是估计隐含类别y的期望值，M步调整其他参数使得在给定类别y的情况下，极大似然估计 P(x,y) P ( x , y ) 能够达到极大值。然后在其他参数确定的情况下，重新估计y，周而复始，直至收敛。

E步（E-step），以当前参数 θ θ 计算 Z Z 的期望值。也就是确定隐含类别变量 c c ，样本所属的分类。我们固定每个类的中心，通过对每一个样本选择最近的分类，以此优化目标函数。

M步（M-step），以当前 Z Z 的值计算使 P(x,y) P ( x , y ) 最大的 θ θ 。求使 J J 函数最小的 u u ，也就是求每个聚类的质心。重新更新每个类的中心点，该步骤可以通过对目标函数求导实现求解 θ θ ，最终可得新的类中心就是类中样本的均值。

这里的隐含类别变量指定方法比较特殊，属于硬指定，从k个类别中硬选出一个给样例（距离哪个聚类近就属于哪个聚类），而不是对每个类别赋予不同的概率。