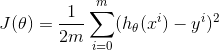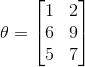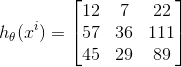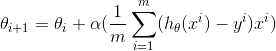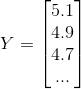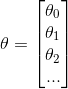python实现线性回归之梯度下降法，梯度下降详解

线性回归的有关概念已在笔者相关文章中进行介绍。本篇内容将介绍梯度下降(BGD)相关内容。

1.梯度下降

梯度下降常用于机器学习中求解符合最小损失函数的模型的参数值，梯度下降也是BP神经网络的核心，本文将介绍批量梯度下降法(BGD)。

如上图所示，梯度下降的过程便是沿梯度方向，按照一定的步伐求解极小(大)值。这里举一个简单的例子，假如你在一座山上，你怎样才能最安全最快速地下山，这里有两个条件，一是安全下山，二是快速下山。答案便是沿着较为陡峭(梯度)的地方，且容易落脚(步伐大小，即学习率)的地方一步一步地下山。

梯度，也就是“山”的斜度，在上图中，便是每个点处的斜率，即导数。下面给出梯度下降的数学公式：

                                                                               

上式中，便是下一步，是当前所处的位置，是步伐大小（学习率），为梯度，也就是对的偏导数。

另外，上式中的为损失函数，也就是描述结果准确程度的函数，在这里，我们定义损失函数为：

                                                                         

理论上，当损失函数取最小值0时，便为最优的结果。对于上述，其实还有其他的损失函数也能很好地发挥作用，但是平方误差损失函数是解决回归问题最常用的手段。

在上式中，表示当前与矩阵的点乘。如：

                                                                         ，

则                                                                 

在上式中，是我们的实际数据。

对求偏导，得：

                                                                       

即最终表达式为：

                                                                  

按照上式，便可求出最终参数。

关于学习率的说明：如果学习率太小，会导致学习时间变长，消耗资源变大。如果学习率太大，可能会越过最低(高)点，误差变大，甚至导致函数无法收敛。

2.python实现

一元参数测试：

import numpy as np

X = mat([1, 2, 3]).reshape(3, 1)  # x为1,2,3
Y = mat([5, 10, 15]).reshape(3, 1)  # y为5,10,15
theta = 1 #初始为1
alpha = 0.1 # 学习率为0.1
for i in range(100):
    theta = theta + np.sum(alpha * (Y - dot(X, theta)) * X.reshape(1, 3))/3 # 公式实现
print(theta)

由代码的初始数据可知，方程应为，下面我们测试theta是否为5：

测试结果正确。

实战：

同样，这里准备了最小二乘法的测试数据，待下面测试结束后，读者可检查结果是否与最小二乘法的结果一致。

数据示例截图如下：

上述数据为某一商品的销售量与售价、服务投资和其它投资的对应关系，即我们要求出：

                                                                 ,,

中，矩阵。

代码如下：

import numpy as np
import pandas as pd
from numpy import dot


dataset = pd.read_csv('C:\\Users\\57105\\Desktop\\data.csv')  # 读入数据
X = dataset.iloc[:, 2: 5]  # x为所有行，2到4列
Y = dataset.iloc[:, 1]  # y为所有行，第1列
theta = np.array([1.0, 1.0, 1.0]).reshape(3, 1)  # theta初始值
alpha = 0.1  # 学习率
temp = theta
X0 = X.iloc[:, 0].values.reshape(60, 1)
X1 = X.iloc[:, 1].values.reshape(60, 1)
X2 = X.iloc[:, 2].values.reshape(60, 1)
Y = Y.values.reshape(60, 1)
for i in range(1000):  # 这里特别注意，在完成一次循环后，整体更新theta
    temp[0] = theta[0] + alpha * np.sum((Y - dot(X, theta)) * X0) / 60.0
    temp[1] = theta[1] + alpha * np.sum((Y - dot(X, theta)) * X1) / 60.0
    temp[2] = theta[2] + alpha * np.sum((Y - dot(X, theta)) * X2) / 60.0
    theta = temp
print(theta)

测试结果：

即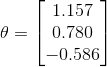，结果与最小二乘法几乎一致，如想再精确，可调整学习率。即,该回归方程反应了商品销售量与售价、服务投资和其它投资的关系。

上述便为梯度下降的相关内容。