Python数据分析可视化Seaborn实例讲解
Seaborn是一种基于matplotlib的图形可视化python libraty。它提供了一种高度交互式界面，便于用户能够做出各种有吸引力的统计图表。 Seaborn其实是在matplotlib的基础上进行了更高级的API封装，从而使得作图更加容易，在大多数情况下使用seaborn就能做出很具有吸引力的图，而使用matplotlib就能制作具有更多特色的图。应该把Seaborn视为matplotlib的补充，而不是替代物。同时它能高度兼容numpy与pandas数据结构以及scipy与statsmodels等统计模式。掌握seaborn能很大程度帮助我们更高效的观察数据与图表，并且更加深入了解它们。 实验数据可以从这里[下载](https://github.com/jakevdp/marathon-data)。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
%matplotlib inlinewarnings.filterwarnings('ignore')def convert_time(s):
h,m,s=map(int,s.split(':'))
return pd.datetools.timedelta(hours=h,minutes=m,seconds=s)data=pd.read_csv('marathon-data.csv',converters={'split':convert_time,'final':convert_time})
data.head()| age | gender | split | final | |
|---|---|---|---|---|
| 0 | 33 | M | 01:05:38 | 02:08:51 |
| 1 | 32 | M | 01:06:26 | 02:09:28 |
| 2 | 31 | M | 01:06:49 | 02:10:42 |
| 3 | 38 | M | 01:06:16 | 02:13:45 |
| 4 | 31 | M | 01:06:32 | 02:13:59 |
data.dtypesage int64
gender object
split timedelta64[ns]
final timedelta64[ns]
dtype: object
添加一列，将时间换算成秒：
data['split_sec']=data['split'].map(lambda x:x.seconds)
data['final_sec']=data['final'].map(lambda x:x.seconds)data.head()| age | gender | split | final | split_sec | final_sec | |
|---|---|---|---|---|---|---|
| 0 | 33 | M | 01:05:38 | 02:08:51 | 3938 | 7731 |
| 1 | 32 | M | 01:06:26 | 02:09:28 | 3986 | 7768 |
| 2 | 31 | M | 01:06:49 | 02:10:42 | 4009 | 7842 |
| 3 | 38 | M | 01:06:16 | 02:13:45 | 3976 | 8025 |
| 4 | 31 | M | 01:06:32 | 02:13:59 | 3992 | 8039 |
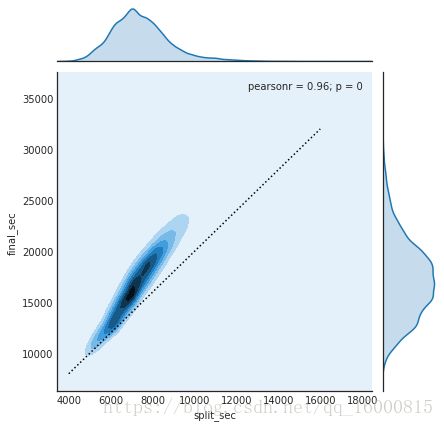
用sns.jointplot可以同时看到两个变量的联合分布与单变量的独立分布，这个图形中使用白色背景。
with sns.axes_style('white'):
g=sns.jointplot('split_sec','final_sec',data,kind='kde')
g.ax_joint.plot(np.linspace(4000,16000),np.linspace(8000,32000),':k')
可以使用六边形块代替频次直方图
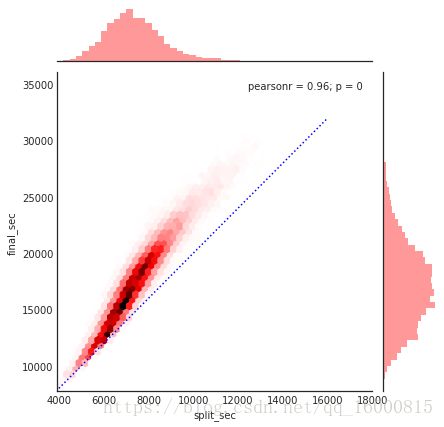
with sns.axes_style('white'):
g=sns.jointplot('split_sec','final_sec',data,kind='hex',color='r')
g.ax_joint.plot(np.linspace(4000,16000),np.linspace(8000,32000),':b')
上图表示的是马拉松前半程成绩与全程成绩的对比。图中的实点线表示一个人全程保持一个速度跑完马拉松,即上半程与下半程耗时相同。然而实际的成绩分布表明,绝大多数人都是越往后跑得越慢(也符合常理)。如果你参加过跑步比赛,那么就一定知道有些人在比赛的后半程速度更快—也就是在比赛中“后半程加速”。
创建一列split_frac来表示前后半程的差异,衡量比赛选手后半程加速或前半程加速的程度。
data["split_frac"]=1-2*data['split_sec']/data['final_sec']data.head()| age | gender | split | final | split_sec | final_sec | split_frac | |
|---|---|---|---|---|---|---|---|
| 0 | 33 | M | 01:05:38 | 02:08:51 | 3938 | 7731 | -0.018756 |
| 1 | 32 | M | 01:06:26 | 02:09:28 | 3986 | 7768 | -0.026262 |
| 2 | 31 | M | 01:06:49 | 02:10:42 | 4009 | 7842 | -0.022443 |
| 3 | 38 | M | 01:06:16 | 02:13:45 | 3976 | 8025 | 0.009097 |
| 4 | 31 | M | 01:06:32 | 02:13:59 | 3992 | 8039 | 0.006842 |
如果前后半程差异系数( split_frac)小于0,就表示这个人是后半程加速型选手。画出差异系数的分布图。
sns.distplot(data['split_frac'],kde=False,color='g')
plt.axvline(0, color="r",linestyle="--")#画垂直x轴的线
上图表示前后半程差异系数分布图，0表示前后半程耗时相同。
sum(data['split_frac']<0)251
在大的4万名马拉松比赛选手中,只有250个人能做到后半程加速。再来看看前后半程差异系数与其他变量有没有相关性。用一个矩阵图pairgrid画出所有变量间的相关性。
g=sns.PairGrid(data,vars=['age','split_sec','final_sec','split_frac'],hue='gender',palette='Set2',\
hue_kws={"marker": ["o", "s"]})
g.map(plt.scatter,alpha=0.8,linewidths=1, s=40)
g.add_legend()
g=sns.PairGrid(data,vars=['age','split_sec','final_sec','split_frac'],hue='gender',palette='hls',\
hue_kws={"marker": ["o", "^"]})
g.map_offdiag(plt.scatter,alpha=0.8,linewidths=1, s=40)#非对角线绘制散点图
g.map_diag(plt.hist)#对角线绘制直方图
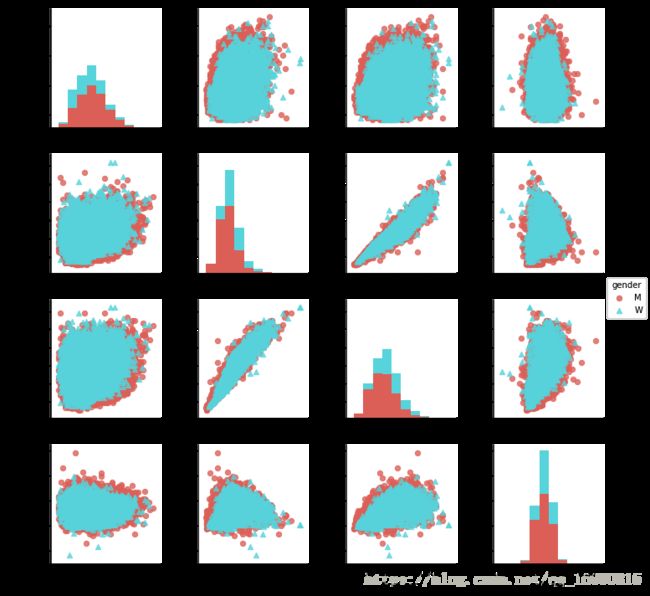
g.add_legend()
g=sns.PairGrid(data,vars=['age','split_sec','final_sec','split_frac'],hue='gender',\
palette=sns.color_palette("hls", 5),hue_kws={"marker": ["s", "d"]})
g.map(plt.scatter,alpha=0.8)
g.add_legend()
从图中可以看出,虽然前后半程差异系数与年龄没有显著的相关性,但是与比赛的最终成绩有显著的相关性:全程耗时最短的选手,往往都是在前后半程尽量保持节奏一致、耗时非常接近的人。
对比男女选手之间的前后半程差异系数的频次直方图如下图所示：
sns.kdeplot(data[data.gender=='M'].split_frac,label='men',shade=True)
sns.kdeplot(data[data.gender=='W'].split_frac,label='women',shade=True)
plt.xlabel('split_frac')
plt.ylim([0,10])
在前后半程耗时接近的选手中,男选手比女选手要多很多!男女选手的分布看起来几乎都是双峰分布。我们将男女选手不同年龄(age)的分布函数画出来,看看会得到什么启示。
用小提琴图( violin plot)画出这两种分布，如下图所示。
小提琴图其实是箱线图与核密度图的结合，箱线图展示了分位数的位置，小提琴图则展示了任意位置的密度，通过小提琴图可以知道哪些位置的密度较高。在图中，白点是中位数，黑色盒型的范围是下四分位点到上四分位点，细黑线表示须。外部形状即为核密度估计（在概率论中用来估计未知的密度函数，属于非参数检验方法之一）。
sns.violinplot('gender','split_frac',data=data,palette=['lightblue','lightpink'])
# 分组的小提琴图
观察这幅图，对比两个由年龄构成函数的小提琴图，在数组中创建一个新列，表示每名选手的年龄段。
data['age_dec']=data['age'].map(lambda x: 10*(x//10))data.head()| age | gender | split | final | split_sec | final_sec | split_frac | age_dec | |
|---|---|---|---|---|---|---|---|---|
| 0 | 33 | M | 01:05:38 | 02:08:51 | 3938 | 7731 | -0.018756 | 30 |
| 1 | 32 | M | 01:06:26 | 02:09:28 | 3986 | 7768 | -0.026262 | 30 |
| 2 | 31 | M | 01:06:49 | 02:10:42 | 4009 | 7842 | -0.022443 | 30 |
| 3 | 38 | M | 01:06:16 | 02:13:45 | 3976 | 8025 | 0.009097 | 30 |
| 4 | 31 | M | 01:06:32 | 02:13:59 | 3992 | 8039 | 0.006842 | 30 |
with sns.axes_style(style='whitegrid'):
sns.violinplot('age_dec','split_frac',data=data,inner='quartile',\
palette="muted")
# 通过hue分组的小提琴图，相当于分组之后又分组
with sns.axes_style(style='whitegrid'):
sns.violinplot('age_dec','split_frac',hue='gender',data=data,inner='quartile',\
palette="muted")
# 分组组合的小提琴图，其实就是hue分组后，各取一半组成一个小提琴图
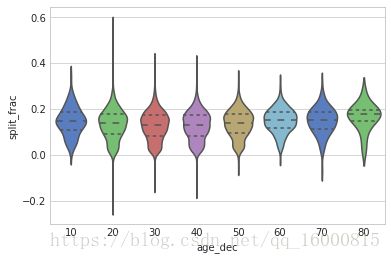
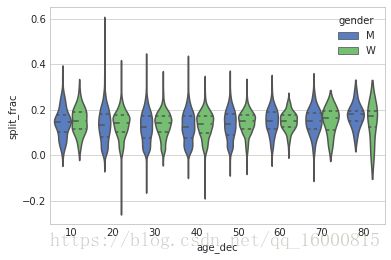
with sns.axes_style(style='whitegrid'):
sns.violinplot('age_dec','split_frac',hue='gender',data=data,split=True,inner='quartile',\
palette=['red','orange'])
上图是用小提琴图表示不同性别，年龄段的前后半程差异系数。通过上图可以看出男女选手的分布差异:20多岁至50多岁各年龄段的男选手的前后半程差异系数概率密度都比同年龄段的女选手低一些(或者可以说任意年龄都如此)。
还有一个令人惊讶的地方是,所有八十岁以上的女选手都比同年龄段的男选手的表现好。这可能是由于这个年龄段的选手寥宴无几,样本太少。
(data.age>80).sum()
7
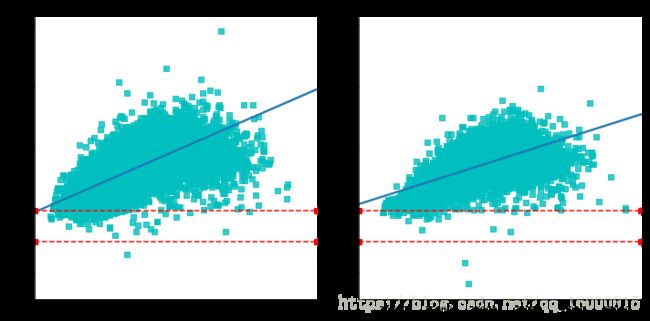
让我们再看看后半程加速型选手的数据:前后半程差异系数与比赛成绩正相关吗?我们可以轻松画出图形。下面用implot为数据自动拟合一个线性回归模型,如下图所示。
g=sns.lmplot('final_sec','split_frac',col='gender',data=data,\
markers='s',scatter_kws=dict(color='c'))
g.map(plt.axhline,y=-0.1,color='r',ls='--')
g.map(plt.axhline,y=0,color='r',ls='--')
从上图明显可以看出前后半程差异系数与比赛成绩正相关，有显著后半程加速的男性选手比赛成绩在15000秒左右，即4小时之内的种子选手。低于这个成绩的选手很少有显著的后半程加速。有显著后半程加速的女性选手比赛成绩大于15000秒，接近20000秒，主要是由于前半程耗时（过多）大于后半程耗时。
下面再从多种图形模式的角度对数据进行探索性分析。
# 绘制箱线图
#在分析数据的时候，箱线图能够直观地识别数据集中的异常值(查看离群点)
ax = sns.boxplot(x=data['final_sec'])
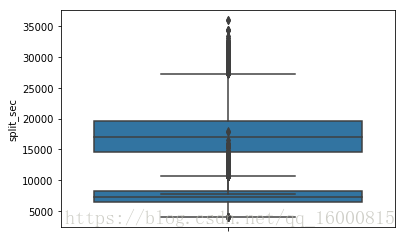
ax = sns.boxplot(x=data['split_sec'])
# 竖着放的箱线图，也就是将x换成y
ax = sns.boxplot(y=data['final_sec'])
ax = sns.boxplot(y=data['split_sec'])
# 分组绘制箱线图，分组因子是gender，在x轴不同位置绘制
ax = sns.boxplot(x="gender", y="final_sec", data=data,palette='RdBu',linewidth=3)
# 分组箱线图，分组因子是gender，不同的因子用不同颜色区分
# 相当于分组之后又分组
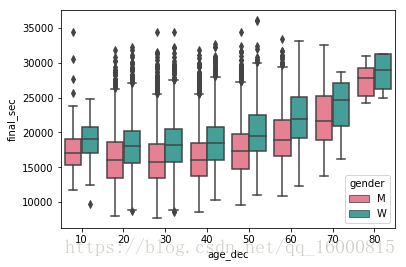
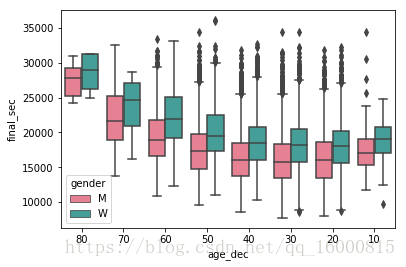
ax = sns.boxplot(x="age_dec", y="final_sec", hue="gender",
data=data, palette="husl")
# 改变x轴顺序，order参数
ax = sns.boxplot(x="age_dec", y="final_sec", hue="gender",
data=data, palette="husl",order=[80,70,60,50,40,30,20,10],linewidth=1.5)
# 散点图
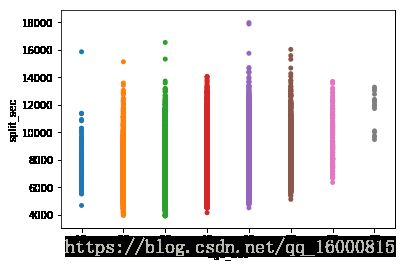
ax1 = sns.stripplot(x=data["age_dec"])
# 分组的散点图
ax = sns.stripplot(x="gender", y="split_sec", data=data)
ax = sns.stripplot(x="age_dec", y="split_sec", data=data)
#散点图通常将重叠。这使得很难看到数据的完整分布。一个简单的解决方案是使用一些随机的“抖动”调整位置（仅沿着分类轴）
## 添加抖动项的散点图，jitter=True
ax = sns.stripplot(x="age_dec", y="split_sec", data=data,jitter=True)
#按照hue=gender分组
ax = sns.stripplot(x="age_dec", y="split_sec",hue='gender',data=data,jitter=True,\
palette=sns.hls_palette(8, l=.5, s=.8))
#分开绘制split=True控制
ax = sns.stripplot(x="age_dec", y="split_sec",hue='gender',data=data,jitter=True,\
palette=sns.hls_palette(8, l=.5, s=.8),split=True)
#按照hue=age_dec分组
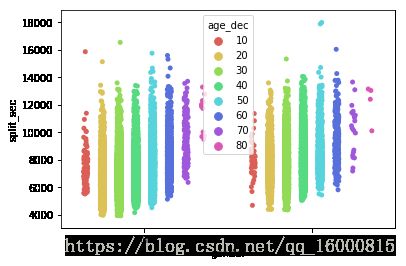
ax = sns.stripplot(x='gender', y="split_sec",hue="age_dec",data=data,jitter=True,\
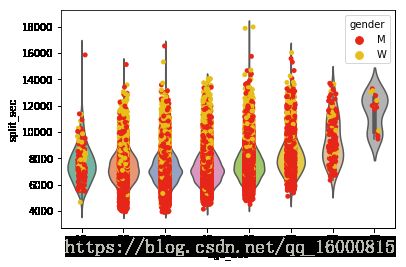
palette=sns.color_palette("hls", 8),split=True)
# 散点图+小提琴图
ax = sns.violinplot(x="age_dec", y="split_sec", data=data,palette='Set2')
ax = sns.stripplot(x="age_dec", y="split_sec",hue='gender',data=data,jitter=True,\
palette=sns.hls_palette(8, l=.5, s=.8))
# 箱线图+散点图
# whis 参数设定是否显示箱线图的离群点，whis=np.inf 表示不显示
ax = sns.boxplot(x="gender", y="split_sec", data=data,whis=np.inf)
ax = sns.stripplot(x="gender", y="split_sec",hue='gender',data=data,jitter=True,\
palette=sns.hls_palette(8, l=.8, s=.8))
#柱状图
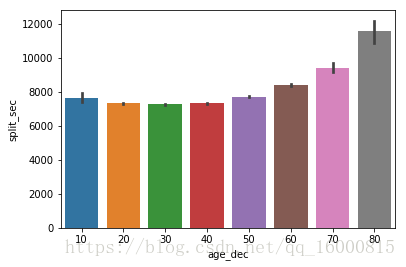
sns.barplot(x="age_dec", y="split_sec",data=data)
#按照hue分组的柱状图,默认统计的是age_dec变量的均值，estimator=np.mean
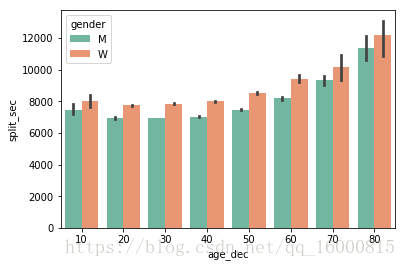
sns.barplot(x="age_dec", y="split_sec",hue='gender',data=data,palette=sns.color_palette("Set2", 10))
#修改默认的统计函数，estimator=max
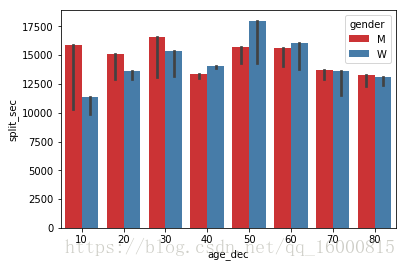
sns.barplot(x="age_dec", y="split_sec",hue='gender',data=data,\
palette=sns.color_palette("Set1", 5),estimator=max)
#频数条形图
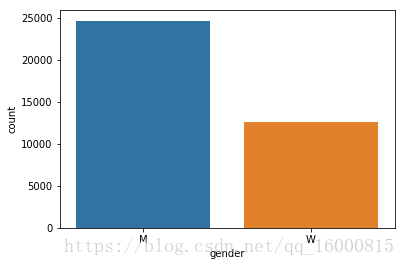
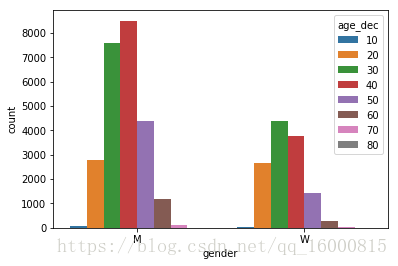
sns.countplot(x="gender", data=data)
sns.countplot(x="gender",hue='age_dec',data=data)
因子图
因子图也是对数据子集进行可视化的方法，你可以通过它观察一个参数在另一个参数间隔中的分布情况
with sns.axes_style(style='ticks'):
g=sns.factorplot(x='age_dec',y='final_sec',hue='gender',data=data,kind='box')
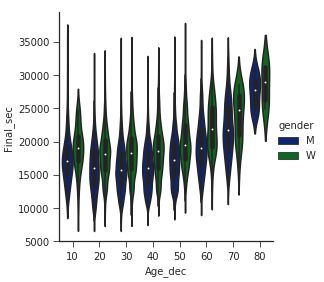
g.set_axis_labels('Age_dec','Final_sec')
with sns.axes_style(style='ticks'):
g=sns.factorplot(x='age_dec',y='final_sec',hue='gender',data=data,kind="violin",\
palette=sns.color_palette("dark"))
g.set_axis_labels('Age_dec','Final_sec')
#col_wrap控制每行画几个图，col控制分开绘图的因子
g = sns.factorplot(x="gender",y='final_sec',col="age_dec", col_wrap=4,palette=sns.color_palette("bright"),\
data=data,kind="violin", size=4, aspect=.8)
g.set_axis_labels('gender','final_sec')
#col_wrap控制每行画几个图,kind控制绘图的类型，size控制图形的大小
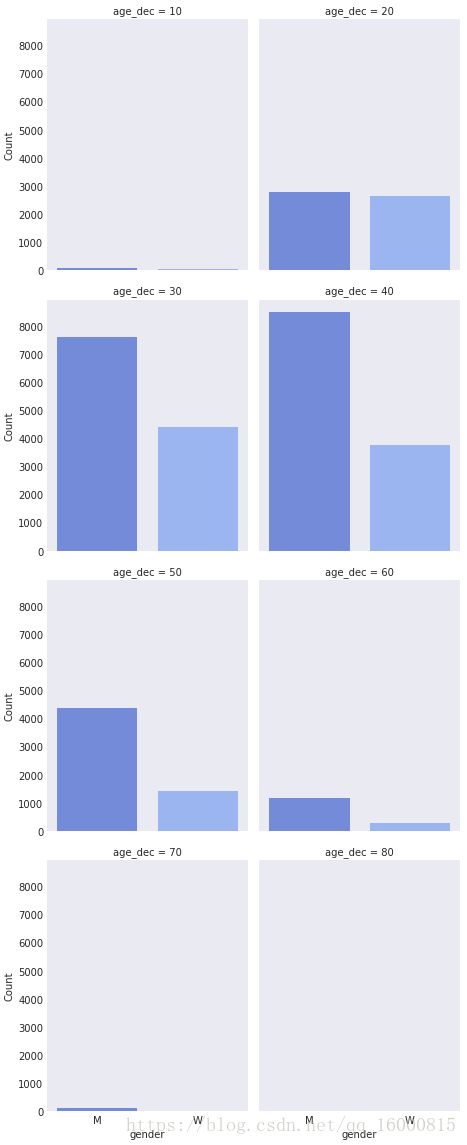
with sns.axes_style('dark'):
g = sns.factorplot(x="gender",col="age_dec", col_wrap=2,palette=sns.color_palette("coolwarm", 7),\
data=data,kind="count", size=4, aspect=.8)
g.set_xlabels('gender')
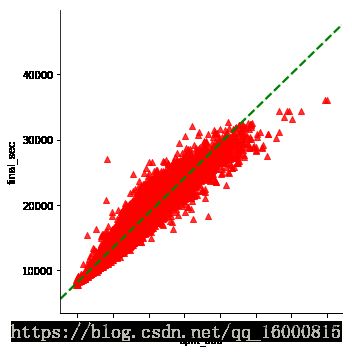
g.set_ylabels('Count')
回归图lmplot
g = sns.lmplot(x="split_sec", y="final_sec", data=data,markers='^',scatter_kws=dict(color='r'),\
line_kws=dict(color='g',linestyle='--'))
# 分组的线性回归图，通过hue参数控制
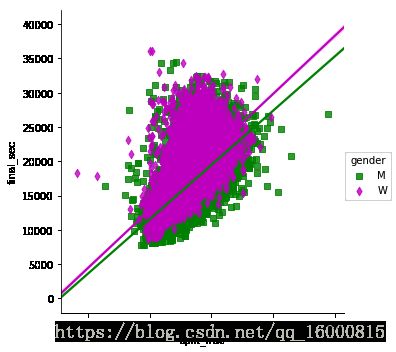
g = sns.lmplot(x="split_frac", y="final_sec",hue="gender", data=data,markers=['s','d'],\
palette=dict(M="g", W="m"))
#按照gender分组，画在两张图上
g = sns.lmplot(x="split_frac", y="final_sec",col="gender", data=data,markers='x',\
palette=sns.set_palette("husl"))
## col+hue 双分组参数，既分组，又分子图绘制，jitter控制散点抖动程度
g = sns.lmplot(x="split_frac", y="final_sec",hue='gender',col="gender", data=data,markers='s',\
line_kws=dict(color='b',linestyle='--'),palette=sns.set_palette("husl",3),x_jitter=.2,aspect=1)
g.map(plt.axvline,x=0,color='r',ls='-')
g = sns.lmplot(x="split_frac", y="final_sec",hue='age_dec',col="age_dec", data=data,markers='d',\
line_kws=dict(color='g',linestyle='--'),palette='Set3',\
col_wrap=4, size=3,x_jitter=.2,aspect=1)
g.map(plt.axvline,x=0,color='y',ls='-')
g.set_axis_labels("split_frac","final_sec")
# 既然col可以控制分组子图的，那么row也是可以控制分组子图的
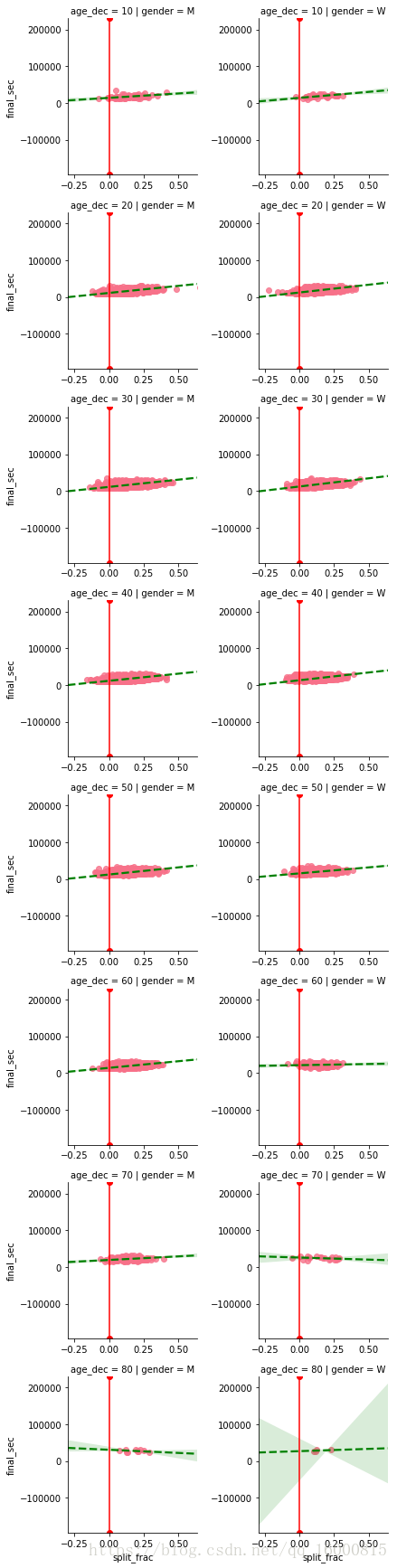
g = sns.lmplot(x="split_frac", y="final_sec",col='gender',row="age_dec",data=data,markers='o',\
line_kws=dict(color='g',linestyle='--'),\
size=3,x_jitter=.1,aspect=1)
g.map(plt.axvline,x=0,color='r',ls='-')
g.set_axis_labels("split_frac","final_sec")
热力图heatmap
sns.heatmap(data[['gender','age','age_dec','split_sec','final_sec','split_frac']].corr())
sns.heatmap(data[['gender','age','age_dec','split_sec','final_sec','split_frac']].corr(),annot=True)
参考资料：
1、python seaborn画图
2、《Python数据科学手册》
3、https://zhuanlan.zhihu.com/p/25909753