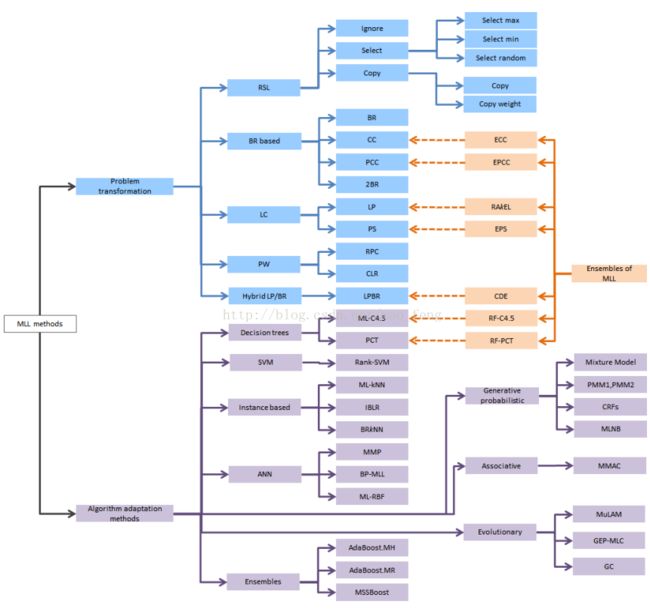
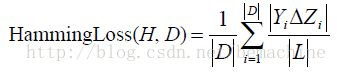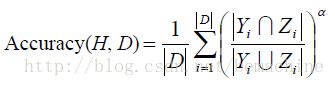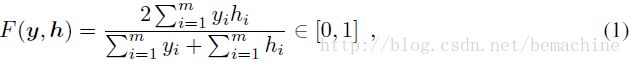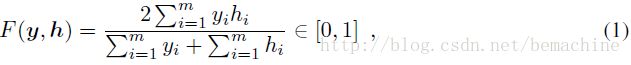分类问题-----多标签（multilabel）、多类别（multiclass）

转自：

大致上，解决multilabel的方法有两种

1）转化问题。把问题转化为一个或多个单目标分类问题，或是回归问题。

2）算法适应。修改学习算法使得能直接处理multilabel的数据。

问题转化方法 dubbed PTx法。包括

• PT1 对有多标签的数据随机选取一个标签
  
   
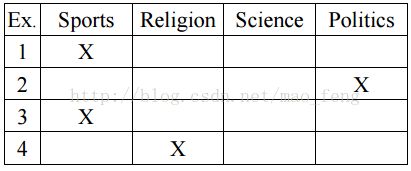
• PT2 直接把标签数大于1的都丢掉
  
  
  
• PT3 对标签集合进行排列组合，即组合好的成为一个新的单标签
  
  
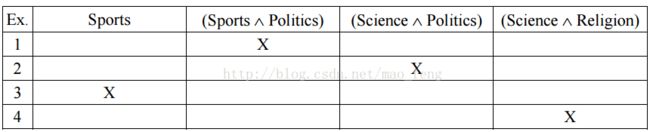
• PT4 把一个含有L个标签的训练转化为L个二分类的训练
  
  
• PT5 把含有多个标签的样本分成多个新样本，用 coverage-based classifier
  
  
•  PT6把含有多个标签的样本对标签集合分成多个新样本
  
  

结论是PT3效果很好，PT4较好也应用比较广泛，PT6由于数据不平衡（如果标签密度太小会导致大量的-1）。

另外，以下几个问题是需要关注和进一步研究的

• Dimensionality Reduction 降维
• Label Dependence 标注依赖
• Active learning 主动学习
• Multi-instance multi-label learning (MIML) 多实例多标签
• Multi-view learning. 多视角
• Multi-task learning (MTL) 多任务
• Hierarchical multi-label classification (HMC) 多层多标签

reference

[1]https://www.researchgate.net/profile/Grigorios_Tsoumakas/publication/273859036_Multi-Label_Classification_An_Overview/links/574575e308aea45ee8539026/Multi-Label-Classification-An-Overview.pdf

[2]https://www.researchgate.net/profile/Sebastian_Ventura/publication/270337594_A_Tutorial_on_Multi-Label_Learning/links/54bcd8460cf253b50e2d697b/A-Tutorial-on-Multi-Label-Learning.pdf

[3] https://users.ics.aalto.fi/jesse/talks/Multilabel-Part01.pdf 

https://users.ics.aalto.fi/jesse/talks/Multilabel-Part02.pdf

几天看了几篇相关的文章， 写篇文章总结一下，就像个小综述一样， 文章会很乱

   1、multilabel classification的用途

         多标签分类问题很常见， 比如一部电影可以同时被分为动作片和犯罪片， 一则新闻可以同时属于政治和法律，还有生物学中的基因功能预测问题， 场景识别问题，疾病诊断等。

  2. 单标签分类

         在传统的单标签分类中，训练集中的每一个样本只有一个相关的标签 l ，这个标签来自于一个不重合的标签集合L，|L| > 1.当|L|=2 时，这就是一个二分类问题，或文本和网页数据的过滤（filtering）问题。当|L| > 2 时是多分类问题。

  3、多标签分类问题的定义

        简单的说就是同一个实例，可以有多个标签， 或者被分为多个类。和多分类的区别是， 多分类中每个实例只有一个标签。下面是几个形式化的定义。

       用代表样本空间，= 为有限标签集合， 我们假设中的样本实例和的一个子集相关,这个子集称作相关标签集。同时补集被认为与x不相关。相关标签集L用向量标识，其中。用表示可能的标签集。

      一个多标签分类器h是一个映射，对每一个实例分配一个分配一个标签子集。因此分类器h的输出是一个向量。

  4、与多标签分类相关/相似的问题

        一个同属于监督学习并和多标签分类很相关的问题就是排序问题（ranking）。排序任务是对一个标签集排序，使得排在前面的标签与相应实例更相关。

      在特定分类问题中，标签属于一个层次结构（hierarchical structure）。当数据集标签属于一个层次结构的时候，我们这个任务为层次分类，如果一个样本与层次结构的多个节点相关， 那么这个任务就被称为层次多标签分类。

     多实例学习（multiple-instance learning）是监督学习的一个变种，用的比较少 ，就不说了。

  5. 多标签分类的方法

       方法基本上分为两种，一种是将问题转化为传统的分类问题，二是调整现有的算法来适应多标签的分类

       常用的转化方法有好几种，比如对每个实例确定或随机的分配一个标签，或只保留只有一个标签的训练样本，然后用传统的多分类方法去训练。这种方法会导致训练样本的损失，所以不推荐使用。还可以将训练样本按每个标签构造一个训练集，每个样本属于或不属于这个标签，对每个标签单独训练一个分类器，然后将多个分类器的结果合成。还有将每个多标签单独看做一个新标签，在一个更多的标签集上做多分类。当多标签样本比较少时，这个方法就比较受限。还有对每个有多个标签的样本，复制该样本，每个样本具有不同的标签，加入训练集后使用覆盖（coverage based）分类法。

     调整的算法也比较多，比如通过调整boost kNN  SVM等实现多分类，这些调整通常也会用到上面的转换。其中调整kNN实现的多标签分类可以加入先验概率，并能对输出标签排序。基于SVM的算法中，有人在训练集中加入了|L|个二分类的训练结果，然后再进行一次分类，这个方法考虑到了不同标签之间的依赖，也是应用栈（Stacking 多个分类器的叠加）的一个特殊情况。还有人利用了相关规则挖掘的方法。

  6. 评价标准

       令D表示多标签评价数据集，有|D|个多标签样本。令H为一个多标签分类器，令为有H基于的预测结果集。

     下面是几个评价标准

      

         

           

   7、 一点感悟

         多标签学习，还有层次结构学习等，多个标签之间一般不是独立(independent)的，所以好的算法要利用标签之间的依赖

         算法训练的时候要么降低cost function 要么学习贝叶斯概率，两种方法本质一样，但表现形式不一样

  8.  其它

       F-measure能比较好的平衡分类器对不同类别实例不同时在不同类上的表现，因此更适合于不平衡的数据。对一个m维二元标签向量 ，对给定的预测，F-measure定义为：

其中由定义，0/0=1

F-measure对应于精度和召回的调和平均。

对于最大化F-measure的方法，为了简化问题一般都基于一些假设， 有人用两个循环给出了精确解

就说这么多吧，不想写了

http://blog.csdn.net/bemachine/article/details/10471383

前言

虽然不是搞分类的，但是还是看看多标签和多分类的区别。为了避免自己的错误理解, 当然是选择原谅他啊…….找正规文档看哇. 以下翻译分别来自scikit-learn.org和 维基 喂鸡百科

国际惯例，贴上来源:

Multiclass and multilabel algorithms

Multi-label classification

Multiclass classification

scikit-learn介绍

多类分类(Multiclass classification): 表示分类任务中有多个类别, 比如对一堆水果图片分类, 它们可能是橘子、苹果、梨等. 多类分类是假设每个样本都被设置了一个且仅有一个标签: 一个水果可以是苹果或者梨, 但是同时不可能是两者

多标签分类(Multilabel classification): 给每个样本一系列的目标标签. 可以想象成一个数据点的各属性不是相互排斥的(一个水果既是苹果又是梨就是相互排斥的), 比如一个文档相关的话题. 一个文本可能被同时认为是宗教、政治、金融或者教育相关话题.

多输出回归(Multioutput classification): 给每个样本一系列的目标值. 可以被想象成对每个数据点预测多个属性, 比如在某个定位的风向和风速

多输出-多分类分类(Multioutput-multiclass classification) 和 多任务分类(Multi-task classification):意味着一个单一的评估器需要处理多个联合分类任务. 这是多标签分类任务(只考虑二院分类)和多类分类任务的推广, 输出格式是2d阵列.

• 每一个输出变量的标签机可以是不同的. 比如一个样本的第一输出变量可以是有限类别中是pear的概率值, 第二个输出变量可能是有限颜色中是blue或者green的概率.
• 这意味着任意的支持多输出多类或者多任务分类任务的分类器, 均支持作为一种特殊情况的多标签分类任务. 多任务分类与多输出分类任务相似, 但是有不同的模型公式.

维基介绍

在机器学习中, 多标签分类(multi-label classification) 和与其极度相关的多输出分类(multi-output classification)是分类问题的变种, 每个实例可能会设置多个标签

多标签分类(Multi-label classification)

• 概念
  多标签分类是多类分类的一般化, 多类分类是将实例精确分类到一个或者多个类别中的单一标签问题, 在多标签问题中, 没有限制说一个实例可以被设置多少个类别.
  正规点讲就是, 多标签分类是找到一个模型将输入x

映射到二值向量 y

• 中.可以将多标签问题转化成一系列的二元分类问题, 然后可以使用多个单标签分类器进行处理.
• 多标签分类采用的算法
  
  1. boosting: AdaBoost.MH和AdaBoost.MR是AdaBoost的多标签数据扩展版本
  2. k近邻:ML-kNN是将k-NN分类器扩展到多标签数据
  3. 决策树
  4. 向量输出的核方法
  5. 神经网络:BP-MLL是反向传播算法的多标签学习问题的扩展

多类分类(Multiclass classification)

• 概念
  在机器学习中, 多类(multiclass)或者多项式(multinomial)分类是将实例分配给一个而非多于两个类别的种类(将实例分类给两类中的一个称为二元分类binary classification). 很多分类算法自身支持多于两类的使用, 剩下的就是二元分类算法了, 这就可以通过很多策略去转换成多项式分类器.
  要将多类分类与多标签分类区分开, 后者是一个类别有多个标签需要被预测
• 多类分类采用的算法
  
  1. 二元分类问题转化
     
     • 一对多(one -vs.- rest)
     • 一对一(one -vs.- one)
  2. 二元问题的扩展
     
     • 神经网络: 多层感知器就是多类问题的扩展，输出N个二值神经元就可以编程多类任务
     • 极限学习机(Extreme Learning Machines (ELM))
     • k近邻: 最古老的非参数分类算法
     • 朴素贝叶斯
     • 决策树
     • 支持向量机
  3. 层级分类
     将多类分类问题的输出空间分割为一个树. 每个父节点被多个子节点分割, 重复这个过程直到每个子节点仅仅代表一类.

1.12. Multiclass and multilabel algorithms

Warning

 

All classifiers in scikit-learn do multiclass classification out-of-the-box. You don’t need to use thesklearn.multiclass module unless you want to experiment with different multiclass strategies.

The sklearn.multiclass module implements meta-estimators to solve multiclass and multilabel classification problems by decomposing such problems into binary classification problems.

• Multiclass classification means a classification task with more than two classes; e.g., classify a set of images of fruits which may be oranges, apples, or pears. Multiclass classification makes the assumption that each sample is assigned to one and only one label: a fruit can be either an apple or a pear but not both at the same time.

• 多类分类是指具有两个以上类的分类任务；例如，对一组水果可能是橙子、苹果或梨进行分类。多类分类的假设是，每个样本被分配到一个和唯一一个标签：一个水果可以是苹果或梨，但不是同时两个。
  

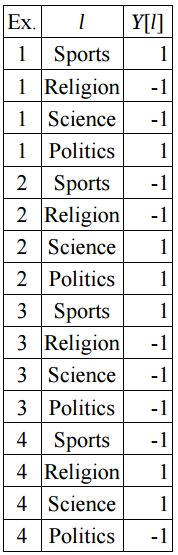
• Multilabel classification assigns to each sample a set of target labels. This can be thought as predicting properties of a data-point that are not mutually exclusive, such as topics that are relevant for a document. A text might be about any of religion, politics, finance or education at the same time or none of these.

• Multilabel classification分配给每个样品一套目标标签。这可以被认为是预测数据集的属性，这些数据集是不相互排斥的，例如与文档相关的主题。文本可能是关于任何宗教、政治、金融或教育的同时，或没有这些。
  

• Multioutput-multiclass classification and multi-task classification means that a single estimator has to handle several joint classification tasks. This is a generalization of the multi-label classification task, where the set of classification problem is restricted to binary classification, and of the multi-class classification task. The output format is a 2d numpy array or sparse matrix.

  The set of labels can be different for each output variable. For instance a sample could be assigned “pear” for an output variable that takes possible values in a finite set of species such as “pear”, “apple”, “orange” and “green” for a second output variable that takes possible values in a finite set of colors such as “green”, “red”, “orange”, “yellow”...

  This means that any classifiers handling multi-output multiclass or multi-task classification task supports the multi-label classification task as a special case. Multi-task classification is similar to the multi-output classification task with different model formulations. For more information, see the relevant estimator documentation.

• Multioutput-multiclass classification and multi-task classification意味着单一的评估器能够具有处理多个节点分类任务的能力。这是多标签分类任务的一个推广，将分类问题限定为二元分类和多类分类任务。输出格式是一个二维的NumPy数组或稀疏矩阵。每个输出变量的标签集可能不同。例如，样品可以分“梨”为输出变量的可能的值，以一组有限的物种如“梨”、“苹果”、“橙色”和“绿色”的第二个输出变量的可能的值，以一组有限的颜色，如“绿色”、“红色”、“橙色”、“黄色”…这意味着任何处理多输出多类或多任务分类任务的分类器都支持作为一种特殊情况的多标签分类任务。多任务分类类似于多输出分类任务，具有不同的模型表示。有关更多信息，请参见相关的估计文档。

All scikit-learn classifiers are capable of multiclass classification, but the meta-estimators offered by sklearn.multiclasspermit changing the way they handle more than two classes because this may have an effect on classifier performance (either in terms of generalization error or required computational resources).

Below is a summary of the classifiers supported by scikit-learn grouped by strategy; you don’t need the meta-estimators in this class if you’re using one of these unless you want custom multiclass behavior:

• Inherently multiclass: Naive Bayes, LDA and QDA, Decision Trees, Random Forests, Nearest Neighbors, setting multi_class='multinomial' in sklearn.linear_model.LogisticRegression.
• Support multilabel: Decision Trees, Random Forests, Nearest Neighbors, Ridge Regression.
• One-Vs-One: sklearn.svm.SVC.
• One-Vs-All: all linear models except sklearn.svm.SVC.

Some estimators also support multioutput-multiclass classification tasks Decision Trees, Random Forests, Nearest Neighbors.

Warning

 

At present, no metric in sklearn.metrics supports the multioutput-multiclass classification task.

1.12.1. Multilabel classification format  多分类数据标签label的转换

In multilabel learning, the joint set of binary classification tasks is expressed with label binary indicator array: each sample is one row of a 2d array of shape (n_samples, n_classes) with binary values: the one, i.e. the non zero elements, corresponds to the subset of labels. An array such as np.array([[1, 0, 0], [0, 1, 1], [0, 0, 0]]) represents label 0 in the first sample, labels 1 and 2 in the second sample, and no labels in the third sample.

Producing multilabel data as a list of sets of labels may be more intuitive. The MultiLabelBinarizer transformer can be used to convert between a collection of collections of labels and the indicator format.

>>> from sklearn.preprocessing import MultiLabelBinarizer
>>> y = [[2, 3, 4], [2], [0, 1, 3], [0, 1, 2, 3, 4], [0, 1, 2]]
>>> MultiLabelBinarizer().fit_transform(y)
array([[0, 0, 1, 1, 1],
       [0, 0, 1, 0, 0],
       [1, 1, 0, 1, 0],
       [1, 1, 1, 1, 1],
       [1, 1, 1, 0, 0]])

1.12.2. One-Vs-The-Rest  一对多

This strategy, also known as one-vs-all, is implemented in OneVsRestClassifier. The strategy consists in fitting one classifier per class. For each classifier, the class is fitted against all the other classes. In addition to its computational efficiency (only n_classes classifiers are needed), one advantage of this approach is its interpretability. Since each class is represented by one and one classifier only, it is possible to gain knowledge about the class by inspecting its corresponding classifier. This is the most commonly used strategy and is a fair default choice.

1.12.2.1. Multiclass learning

Below is an example of multiclass learning using OvR:

>>> from sklearn import datasets
>>> from sklearn.multiclass import OneVsRestClassifier
>>> from sklearn.svm import LinearSVC
>>> iris = datasets.load_iris()
>>> X, y = iris.data, iris.target
>>> OneVsRestClassifier(LinearSVC(random_state=0)).fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

1.12.2.2. Multilabel learning

OneVsRestClassifier also supports multilabel classification. To use this feature, feed the classifier an indicator matrix, in which cell [i, j] indicates the presence of label j in sample i.

Examples:

• Multilabel classification

1.12.3. One-Vs-One

OneVsOneClassifier constructs one classifier per pair of classes. At prediction time, the class which received the most votes is selected. In the event of a tie (among two classes with an equal number of votes), it selects the class with the highest aggregate classification confidence by summing over the pair-wise classification confidence levels computed by the underlying binary classifiers.

Since it requires to fit n_classes * (n_classes - 1) / 2 classifiers, this method is usually slower than one-vs-the-rest, due to its O(n_classes^2) complexity. However, this method may be advantageous for algorithms such as kernel algorithms which don’t scale well with n_samples. This is because each individual learning problem only involves a small subset of the data whereas, with one-vs-the-rest, the complete dataset is used n_classes times.

1.12.3.1. Multiclass learning

Below is an example of multiclass learning using OvO:

>>> from sklearn import datasets
>>> from sklearn.multiclass import OneVsOneClassifier
>>> from sklearn.svm import LinearSVC
>>> iris = datasets.load_iris()
>>> X, y = iris.data, iris.target
>>> OneVsOneClassifier(LinearSVC(random_state=0)).fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])

References:

[1]	“Pattern Recognition and Machine Learning. Springer”, Christopher M. Bishop, page 183, (First Edition)

1.12.4. Error-Correcting Output-Codes

Output-code based strategies are fairly different from one-vs-the-rest and one-vs-one. With these strategies, each class is represented in a euclidean space, where each dimension can only be 0 or 1. Another way to put it is that each class is represented by a binary code (an array of 0 and 1). The matrix which keeps track of the location/code of each class is called the code book. The code size is the dimensionality of the aforementioned space. Intuitively, each class should be represented by a code as unique as possible and a good code book should be designed to optimize classification accuracy. In this implementation, we simply use a randomly-generated code book as advocated in [3] although more elaborate methods may be added in the future.

At fitting time, one binary classifier per bit in the code book is fitted. At prediction time, the classifiers are used to project new points in the class space and the class closest to the points is chosen.

In OutputCodeClassifier, the code_size attribute allows the user to control the number of classifiers which will be used. It is a percentage of the total number of classes.

A number between 0 and 1 will require fewer classifiers than one-vs-the-rest. In theory, log2(n_classes) / n_classes is sufficient to represent each class unambiguously. However, in practice, it may not lead to good accuracy since log2(n_classes) is much smaller than n_classes.

A number greater than than 1 will require more classifiers than one-vs-the-rest. In this case, some classifiers will in theory correct for the mistakes made by other classifiers, hence the name “error-correcting”. In practice, however, this may not happen as classifier mistakes will typically be correlated. The error-correcting output codes have a similar effect to bagging.

1.12.4.1. Multiclass learning

Below is an example of multiclass learning using Output-Codes:

>>> from sklearn import datasets
>>> from sklearn.multiclass import OutputCodeClassifier
>>> from sklearn.svm import LinearSVC
>>> iris = datasets.load_iris()
>>> X, y = iris.data, iris.target
>>> clf = OutputCodeClassifier(LinearSVC(random_state=0),
...                            code_size=2, random_state=0)
>>> clf.fit(X, y).predict(X)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
       0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1,
       1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 2, 2, 2, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
       2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 1, 1, 2, 2, 2,
       2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])