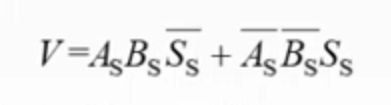2.2 定点数的表示和运算
定点数的表示 1 无符号数，若机器字长是8位，则表示的数据范围是0~255
2 有符号数，通过“0”表示正号，“1”表示符号，来表示数据。有符号数的机器表示有原码，反码，补码，移码。
定点表示，机器数中的小数点位置是固定不变的，小数点不再使用“。”表示，而是约定它的位置。这里有两种简单的约定，将小数点的位置固定在数据的最高位之前，或固定在最低位之后。一般称前者为定点小数后者为定点整数。
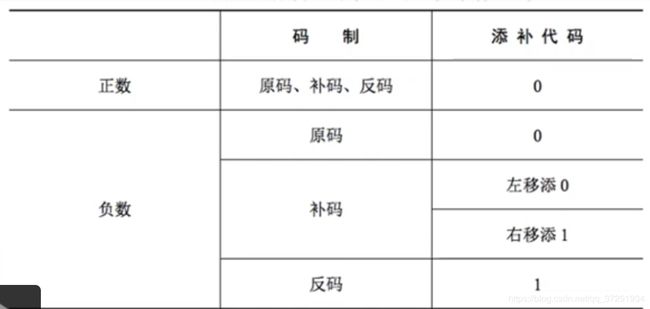
原码 [+0]原=00000和[-0]原=10000
补码 正数的补码和原码相同。负数是，原码符号位不变，数值部分按位取反，末位加1.真值零的补码表示唯一，[+0]补和[-0]补=0.0000
反码 [+0]反=0.0000和[-0]反1.1111
移码 因为补码不能直观的看出数之间的大小关系所以引入了移码，移码就是在真值x上加上一个常数(偏置值)，通常这个常数取
，[x]移=2^n+x（
,其中机器字长为n+1）。移码中的0表示唯一[+0]移[-0]移=1000...0（n个“0”）。一个真值得移码和补码仅差一个符号位，[x]补的符号位取反即得[x]移。移码保持了数据原有的大小顺序，移码大真值就大，移码小真值就小。
定点数的算术移位
对象是有符号数，在移位过程中符号位保持不变。
定点数的逻辑移位
不管是左移还是右移，都填0
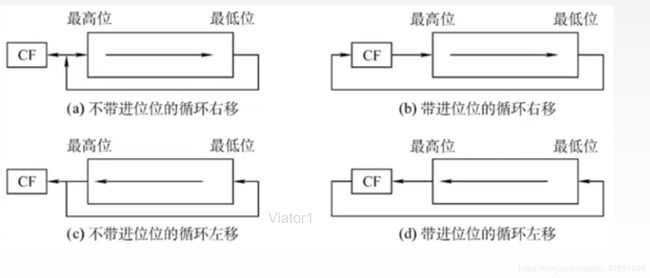
循环移位
[-B]补的求法是[B]补连同符号位一起取反加1（无论正，负）
符号扩展，比如在将8位数和32位数相加之前，必须将8位数转换成32位数的形式。
正数，原有形式的符号位移动到新形式的符号位上，新表示形式的所有附加位都用0填充。
负数，原码表示负数的符号扩展方法与正数相同。补码是，原有形式的符号位移动到新形式的符号位上，新表示形式的所有附加位都用1（对于整数）或0（对于小数）进行填充。反码，原有形式的符号位移动到新形式的符号位上，新表示形式的所有附加位都用1填充。
溢出的判断
1> 采用一位符号位
设A的符号为As，B的符号为Bs，运算结果的符号为Ss
若V=0，表示无溢出，V=1，表示有溢出
2> 采用双符号位
双符号位法也称模4补码。这里设置两个符号位。S1和S2。
S1S2=00，表示结果为正数，无溢出。
S1S2=01，表示结果为正溢出。
S1S2=10，表示结果负溢出。
S1S2=11，表示结果为负数，无溢出。
，V=0，表示无溢出，V=1，表示有溢出。
3> 采用一位符号位根据数据位的进位情况判断溢出
若符号位的进位Cs与最高位的进位C1相同，则说明没有溢出，否则表示发生溢出。
定点数的乘法
1> 原码一位乘法
特点是符号位与数值位分开求
2> 补码一位乘法（Booth算法）
是一种有符号数的乘法
定点数的除法
1> 原码除法运算（不恢复余数法）
商符和商值分开。
2> 补码除法运算（加减交替法）
符号位和数值位一起参与运算
强制类型转换
相同类型的有符号数向无符号数转换或者无符号数向有符号数转换，保存位值不变，仅改变解释这些位的方式。
当大字节变量向小字节变量强制类型转换时，系统把多余的高位字长部分直接截断，低位直接赋值。
短字长到长字长转换，在位值相等的条件下补充高位的符号位，类似符号扩展。