【常用算法思路分析系列】字符串高频题集
本文是【常用算法思路分析系列】的第二篇，分析字符串相关的高频题目。第一篇是关于排序相关的高频题，还没有看的同学请移步：【常用算法思路分析系列】排序高频题集
1、KMP字符匹配
对于两棵彼此独立的二叉树A和B，请编写一个高效算法，检查A中是否存在一棵子树与B树的拓扑结构完全相同，即给定两棵二叉树的头结点A和B，请返回一个boolean值，代表A中是否存在一棵同构于B的子树。上述其实就是一个字符匹配的问题，我们将A、B两棵二叉树进行遍历，得到一个字符串，就是判断B串是否是A串的子串。而字符匹配常用的算法采用KMP来实现。关于KMP算法分析，我这篇文章中有详细的介绍：我眼中的KMP。
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
public boolean chkIdentical(TreeNode A, TreeNode B) {
String s1 = getSerializString(A);
String s2 = getSerializString(B);
return kmp(s1,s2);
}
//遍历二叉树得到字符串
private static String getSerializString(TreeNode head){
if(head == null)
return null;
StringBuilder sb = new StringBuilder();
sb.append(head.val).append(getSerializString(head.left)).append(getSerializString(head.right));
return sb.toString();
}
public static boolean kmp(String str1,String str2){
char[] strA = str1.toCharArray();
char[] strB = str2.toCharArray();
int[] next = getNextArray(strB);
int i,k;
for(i = 0,k = 0; i < strA.length; i++){
while(k > 0 && strA[i] != strB[k])
k = next[k-1];
if(strA[i] == strB[k]){
k++;
}
/*
* 注意，这里和求next数组有一点区别，因为kmp里面是主串和子串进行比较，当子串最后一个元素都相等的时候，k就相当于是子串和主串相同的公共部分长度，
* 而对于求next数组中的方法来说，相当于是自身和自身进行比较
*/
if(k == strB.length){
return true;
}
}
return false;
}
private static int[] getNextArray(char[] chs){
int i;//字符数组的下表指示器
int k;//前一个字符处的最大公共（相等）前、后缀子串的长度
int[] next = new int[chs.length];
for(i = 1,k = 0; i < chs.length; i++){
while(k > 0 && chs[i] != chs[k])
k = next[k - 1];
if(chs[i] == chs[k]){
k++;
}
next[i] = k;
}
return next;
}
/** 解法二：暴力破解法
* 时间复杂度为O(m*n)，m、n分别为strA.length()和strB.length()
* @param strA
* @param strB
* @return
*/
private static boolean compareIdentical(String strA,String strB){
int indexA,indexB;
char[] charA = strA.toCharArray();
char[] charB = strB.toCharArray();
for(int i = 0; i < charA.length; i++){
if(charA[i] == charB[0]){
indexA = i;
for(indexB = 0; indexB < charB.length && indexA < charA.length; indexB++){
if(charA[indexA++] != charB[indexB])
break;
}
if(indexB >= charB.length){//表示已经匹配到
return true;
}
}
}
return false;
}2、判断是否为变形词
对于两个字符串A和B，如果A和B中出现的字符种类相同且每种字符出现的次数相同，则A和B互为变形词，请设计一个高效算法，检查两给定串是否互为变形词。
以int[]数组作为哈希表，字符的ASCII值作为下标进行映射。先以A字符串的每个字符值作为下标进行映射，令其对应位置的值+1，遍历完后，再使用B字符值进行遍历，先查看对应位置是否为0，如果为0了，表示A中没有该字符（或少于B中的字符数量），如果不为0，则将对应位置的值-1。
/**
* 以int[]数组作为哈希表，字符作为下标进行映射。
* 时间复杂度为O(N)，空间复杂度为O(N)
* @param A
* @param lena
* @param B
* @param lenb
* @return
*/
public static boolean chkTransform(String A, int lena, String B, int lenb) {
if(A == null || B == null || lena != lenb){
return false;
}
char[] charA = A.toCharArray();
char[] charB = B.toCharArray();
int[] map = new int[256];
for(int i = 0; i < charA.length; i++){
map[charA[i]]++;
}
for(int i = 0; i < charA.length; i++){
if(map[charB[i]]-- == 0)//这里只能是--在后面
return false;
}
return true;
}
/**
* 暴力破解法
* @param A
* @param lena
* @param B
* @param lenb
* @return
*/
public static boolean chkTransform2(String A, int lena, String B, int lenb) {
if(A == null || B == null || lena != lenb){
return false;
}
Map mapA = new HashMap();
Map mapB = new HashMap();
char[] charA = A.toCharArray();
char[] charB = B.toCharArray();
char key;
for(int i = 0; i < charA.length; i++){
key = charA[i];
if(mapA.containsKey(key)){
mapA.put(key, mapA.get(key) + 1);
}else{
mapA.put(key, 1);
}
}
for(int i = 0; i < charB.length; i++){
key = charB[i];
if(mapB.containsKey(key)){
mapB.put(key, mapB.get(key) + 1);
}else{
mapB.put(key, 1);
}
}
if(mapA.size() != mapB.size()){
return false;
}
Set keys = mapA.keySet();
for(Character ch : keys){
if(mapA.get(ch) != mapB.get(ch)){
return false;
}
}
return true;
} 3、旋转词
如果一个字符串str，把字符串str前面任意的部分挪到后面去形成的字符串叫做str的旋转词。比如str="1234"，str的旋转词有"1234"，"2341"，"3412"，"4123"。给定两个字符串a和b，请判断a和b是否互为旋转词。
举例：
a="cdab"，b="abcd"，返回true；
a="1ab2"，b="ab12"，返回false；
最优解时间复杂度为O(n)，解题思路如下：
（1）判断str1和str2长度是否相等；
（2）如果长度相等，生成 str1 + str1 的大字符串；
（3）用KMP算法判断大字符串中是否包含有字符串str2；
举例说明：
str1 = "1234";
生成str1+str1大字符串为：str1 + str1 = "12341234";
如果str1的长度为N，在str1 + str1的大字符串中，任意一个长度为N的子串都是str1的旋转词！此时只需要判断str2是否为str1+str1的子串即可。
如上的str1+str1中，子串"
1234
1234"、"12341234"、"12341234"、"12341234"、"12341234"。（使用KMP算法查找）。
public boolean chkRotation(String a, intlena, String b, intlenb) {
if(a == null|| b == null|| lena != lenb) {
return false;
}
String b2 = b + b;
return kmp(b2, a);//kmp（）方法为上面的KMP算法
}4、字符串逆序调整
给定一个字符串str，请在单词间做逆序调整。
举例：
"pig loves dog" 逆序成 "dog loves pig"
"I'm a student" 逆序成 "student a I'm"
解题思路如下：
（1）实现将字符串局部所有字符逆序的函数fun，如：
...........fedcba................
从两端开始，先将第一个与最后一个交换（f、a交换），再e与b交换，d与c交换...直到中间位置停止交换过程
（2）利用上面的函数fun将字符串所有字符逆序
"pig loves dog" --> "god sevol gip"
（3）找到逆序后的字符串中每一个单词的区域，利用fun将每一个单词的区域逆序；
"god sevol gip" --> "dog loves pig"
public class CharTest {
public static void main(String[] args) {
String str = new String("pig loves dog");
String res1 = reverseStr(str);
/* 不推荐的方式
String[] ss = res1.split(" ");
String res = "";
for(String s : ss){
res += reverseStr(s) + " ";
}
res = res.trim();
*/
String res = ""; //存放反转的结果
char[] chs = res1.toCharArray();
String tempstr = "";//暂存字符串中的单词区域
for(int i = 0; i < chs.length; i++){
char c = chs[i];
if(c == ' ' || i == chs.length - 1){//如果当前是空字符或到了最右一个字符，表示前面已经是一个单词了
if(i == chs.length - 1 && c != ' '){//如果遍历到了最后一个字符，并且最后一个字符不为空
tempstr += c;
c = ' ';
}
if(!"".equals(tempstr)){
if(!"".equals(res)){
res += c + reverseStr(tempstr);
}else{
res += reverseStr(tempstr);
}
tempstr = "";
}
}else{//属于同一个单词
tempstr += c;
}
}
System.out.println(res);
}
/**
* 实现字符串所有字符逆序函数
* @param src
* @return
*/
private static String reverseStr(String src){
char temp;
char[] chars = src.toCharArray();
for(int i = 0,j = chars.length - 1; i < j; i++,j--){
temp = chars[i];
chars[i] = chars[j];
chars[j] = temp;
}
return String.valueOf(chars);
}
}5、字符串部分整体交换
给定一个字符串str，和一个整数i，i代表str中的位置，将str[0,i]移到右侧，str[i+1, N-1]移到左侧。
举例：
str="ABCDE", i=2，将str调整为"DEABC"，要求：时间复杂度为O(n)，空间复杂度为O(1)
解题思路如下：
（1）将str[0...i]部分的字符逆序（i=2）
A B C D E --> C B A D E
（2）将str[i+1~N-1]部分的字符逆序
C B A D E --> C B A E D
（3）将str整体的字符逆序
C B A E D --> D E A B C
public class CharTest2 {
public static void main(String[] args) {
String str = new String("i love you");
String res = reverPartStr(str,2);
System.out.println("==========>" + res);
}
/**
* 实现字符串所有字符逆序函数
* @param src
* @return
*/
private static String reverseStr(String src){
char temp;
char[] chars = src.toCharArray();
for(int i = 0,j = chars.length - 1; i < j; i++,j--){
temp = chars[i];
chars[i] = chars[j];
chars[j] = temp;
}
return String.valueOf(chars);
}
/**
* 实现对字符串给定分割位置i，进行左右两部分交换
* @param src
* @param i
* @return
*/
private static String reverPartStr(String src,int i){
if(i >= (src.length() - 1)){
return src;
}
String str1 = src.substring(0, i+1);
String str2 = src.substring(i+1, src.length());
String res = reverseStr(str1) + reverseStr(str2);
return reverseStr(res);
}
}总结：可以看到，与字符串交换相关的题目，大部分是活用局部逆序函数组合的一个过程。可用如下过程图展示：
6、字符拼接得到最小字典序字符串
给定一个字符串类型的数组strs，请找到一种拼接顺序，使得将所有字符串拼接起来组成的大字符串是所有可能性中字典顺序最小的，并返回这个大字符串。
举例：
strs={"abc","de"}，可以拼接成"abcde"，"deabc"，但前者字典顺序更小，所以返回"abcde"。
strs={"b","ba"}，可以拼接成"bba"，"bab"，但后者字典序更小，所以返回"bab"。
最优解时间复杂度为O(N*logN)，其实质是一种排序，解题思路如下：
错误方案：根据单独每个字符串的字典顺序排序
{"abc", "de"} -------------根据数组中的每个字符串的字典序排序-----------> {"abc", "de"} ，排完后最后拼接成了“abcde”，答案虽然对了，但是过程是错误的。再举个例子：
{"ba" ,"b"} -------------根据数组中的每个字符串的字典序排序-----------> {"b" , "ba"}，排完后拼接成了“bba”，而实际上字符串“bab”才是字典序最小的。
如果str1+str2 < str2 + str1，则str1放在前面，否则str2放在前面。
这两种方案的区别在于，正确方案是在让数组中两个字符串先拼接再比较它们拼接后的字典顺序大小，二错误方案是直接比较两个字符串的字典序大小。
剑指Offer中有一道类似的题： 把数组排成最小的数。
public static String PrintMinNumber(int [] numbers) {
if(numbers == null){
return null;
}
StringBuilder sb = new StringBuilder();
String pre,last;
int temp;
for(int i = 0; i < numbers.length; i++){
for(int j = i + 1; j < numbers.length; j++){
pre = numbers[i] + "" + numbers[j]; //转换成字符串的形式
last = numbers[j] + "" + numbers[i];
if(pre.compareTo(last) > 0){ //比较组合之后的ab和ba
temp = numbers[i];
numbers[i] = numbers[j];
numbers[j] = temp;
}
}
sb.append(numbers[i]);
}
return sb.toString();
}7、空格替换
给定一个字符串str，将其中所有空格字符替换成"%20"，假设str后面有足够的空间。
解题思路：
比如字符串“a b c”，如下思路：
代码如下：
public String replaceSpace(String iniString, int length) {
if(iniString == null || length > iniString.length()){
return null;
}
char[] chs = iniString.toCharArray();
int num = 0;
for(int i = 0; i < length; i++){
if(chs[i] == ' ')
num++;
}
int newlength = length + 2 * num;
for(int i = length - 1, j = newlength - 1; i <= j - 2 && i >= 0;){
if(chs[i] != ' '){
chs[j] = chs[i];
i--;
j--;
}else{
chs[j--] = '0';
chs[j--] = '2';
chs[j--] = '%';
i--;
}
}
return String.valueOf(chs);
}
public String replaceSpace(String iniString, int length) {
if(iniString == null || length > iniString.length()){
return null;
}
char[] chs = iniString.toCharArray();
int num = 0;
for(int i = 0; i < length; i++){
if(chs[i] == ' ')
num++;
}
int newlength = length + 2 * num;
char[] newChs = new char[newlength]; //新开辟一个数组
for(int i = 0, j = 0; i < length && j < newlength; i++){
if(chs[i] != ' '){
newChs[j++] = chs[i];
}else{
newChs[j++] = '%';//此时是从前往后的顺序，因此加入的顺序是%20
newChs[j++] = '2';
newChs[j++] = '0';
}
}
return String.valueOf(newChs);
}8、合法括号序列判断
对于一个字符串，请设计一个算法，判断其是否为一个合法的括号串。
给定一个字符串A和它的长度n，请返回一个bool值代表它是否为一个合法的括号串。
测试样例：
"(()())",6
返回：true
测试样例：
"()a()()",7
返回：false
解题思路：
（1）用一个整形变量num代表'('出现次数和')'出现次数的差值；
（2）遍历过程中，如果遇到'('，则num++;
（3）遍历过程中，如果遇到')'，则num--;
（4）遍历过程中，如果num < 0，直接返回false；
（5）遍历过程中，如果如果遇到非括号字符，此时，判断num == 0 ?，如果为0，则直接返回false；
（6）遍历到最后，如果num != 0，则返回false。
代码如下：（时间复杂度为O(N)，空间复杂度为O(1)）
public static boolean chkParenthesis(String A, int n) {
if(A == null)
return false;
int num = 0;
char[] chs = A.toCharArray();
for(int i = 0; i < chs.length; i++){
if(chs[i] == '('){
num++;
}else if(chs[i] == ')'){
num--;
}else{//非括号字符时，如果num==0，匹配不成功
if(num == 0)
return false;
}
if(num < 0)
return false;
}
if(num != 0)
return false;
return true;
}9、最长无重复字符子串
对于一个字符串,请设计一个高效算法，找到字符串的最长无重复字符的子串长度。
解题思路：
从头开始变量字符串，需要用到两个变量：
（1）哈希表map：统计每种字符之前最近一次出现的位置；
（2）整形变量pre：代表以s[i-1]结尾的情况下，最长无重复子串的长度。
思路图解如下：
所以第一步就是先把位置A和位置B的值求出来，同时要记得更新最近出现的字符位置。代码如下：
我自己按上面思路写的代码：
public static int longestSubstring(String A, int n) {
if(A == null)
return 0;
char[] chs = A.toCharArray();
Map map = new HashMap();
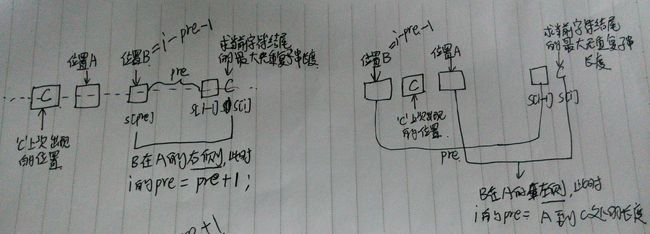
int pre = 1;//注意！！！我们是从第二个字符开始，那以第一个字符结尾的最长无重复子串长度就是1
map.put(chs[0], 0);
int posA;//当前所求结点往左最长可达到无重复子串的位置
int posB;//前一个结点所求结点往左最长可达到无重复子串的位置
int max = pre;//记录最长无重复子串的最大长度
for(int i = 1; i < chs.length; i++){
if(map.containsKey(chs[i])){
posA = map.get(chs[i]) + 1;
}else{
posA = 0;
}
map.put(chs[i], i);//更新这种字符的最近位置
posB = i - pre - 1;
if(posB >= posA){//B在A的右边
pre++;
}else{
pre = i - posA + 1;
}
if(pre > max)
max = pre;
}
return max;
} 下篇【常用算法思路分析系列】将是针对队列相关。