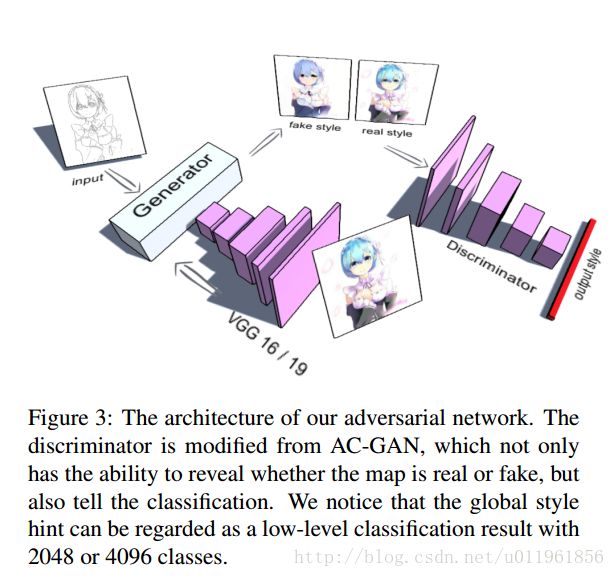
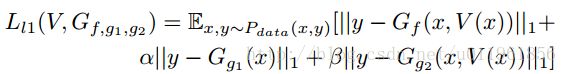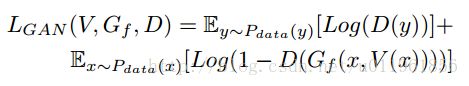Style Transfer for Anime Sketches with Enhanced Residual U-net and Auxiliary Classifier GAN
网络结构
本文的GAN网络结构为:
生成网络的输入为需要风格转换的图像即input,以及风格特征.采用VGG16/19的fc1层,提取风格图像的特征,风格特征为4096维的向量.
生成网络结构和目标函数
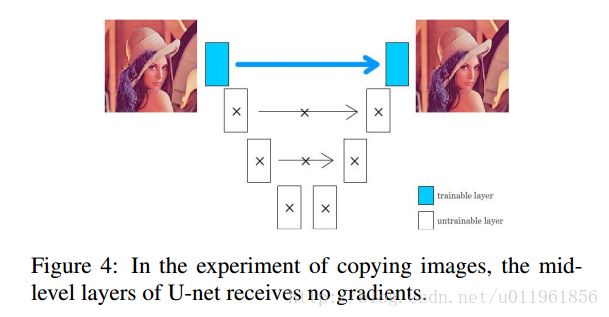
文章试验发现,如果u-net可以使用底层的网络学习到特征,那么高层的网络就不会去学习,如图4所示,u-net网络的输入输出都为同一张图像,也就是实现复制图像的功能.由于输入输出是相同的,损失函数会立刻变为0.这是因为encoder的第1层发现可以通过skip connection, 简单地直接传递所有的特征到decoder的最后一层,以最小化损失函数.这样,无论训练多少次,中间层的网络都没有任何梯度值,也就是中间网络没有作用了.
对于u-net的decoder层,特征可以来源于更高的层或者skip connection层.在训练的时候,这些层可以选择别的层的输出,这可以通过非线性函数实现,以最小化损失函数.
在图4的实验中,采用高斯随机初始化u-net网络参数,encoder的第1层的输出完全足够表达输入特征,而encoder的第2到最后一层的输出更多的是噪声特征,因此网络放弃了这些noisy feature.
对于一个新的初始化的u-net网络,如果直接将4096维的特征向量到u-net的中间层,那么这些层会非常noisy. 如上面分析,如果中间层网络噪声化严重,那么u-net网络会放弃这些层,结果就是,这些层不能得到任何的梯度,我们将这些层称为lazy layer.
受LeNet,GooLeNe的启发,我们使用残差网络,如图5.
将额外的loss添加到可能为lazy的层,那么无论这些层多么noisy, unet都不会放弃这些网络层,并且在整个训练过程中,这些层都会得到稳定的梯度. 这样,便可以在中间层添加一些含有特征信息的,甚至noisy hint的特征.本文实现了两个额外的loss,分别在Guide decoder 1和Guide decoder 2中,以消除中间层的梯度消失.
生成网络损失函数定义为:
文章还提出,对于色彩分布,往中间层添加灰度特征会有所改善,因此使用函数 T(y) 将y转换为灰度图像,最后的loss为:
生成网络整体结构为:
Guider Decoder 1输入为u-net的encoder的输出,为 16×16×256 的特征向量,输出为 512×512×1 的灰度图像.
Guider Decoder 2 输入为u-net的encoder的输出与VGG16的输出的串联特征,为 16×16×512 的特征向量,输出为 512×512×3 的彩色图像.
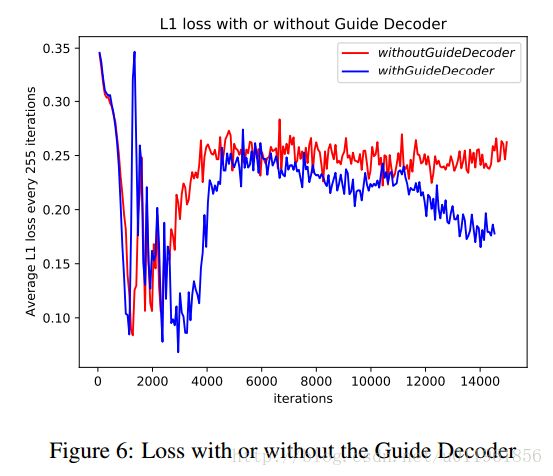
添加效果对比如图6,7所示.
判别网络结构和目标函数
总的目标函数为: