使用tensorflow进行房价预测
在回归问题中,我们的目标是预测一个连续值的输出,如价格或概率。将此与一个分类问题进行对比,我们的目标是预测一个离散的标签(例如,图片包含一个苹果或橙子)。
本示例建立了一个模型来预测波士顿郊区在20世纪70年代中期的中值价格。为了做到这一点,我们将提供模型与郊区的一些数据,如犯罪率和地方物业税税率。
使用tensorflow的高级API进行建模。
import tensorflow as tf
from tensorflow import keras
import numpy as np
boston_housing=keras.datasets.boston_housing
#提前下载好的数据
(train_data,train_label),(test_data,test_label)=boston_housing.load_data("F://data//machine_learning//回归数据//波士顿房价/boston_housing.npz")
print(train_data[0].shape,test_data[0])
#shuffle数据集
order=np.argsort(np.random.random(train_label.shape))
train_data=train_data[order] #特征
train_label=train_label[order] #标签
#使用pandas处理数据并显示
import pandas as pd
column_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT']
df=pd.DataFrame(train_data,columns=column_names)
df.head()数据格式如下:
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.07875 | 45.0 | 3.44 | 0.0 | 0.437 | 6.782 | 41.1 | 3.7886 | 5.0 | 398.0 | 15.2 | 393.87 | 6.68 |
| 1 | 4.55587 | 0.0 | 18.10 | 0.0 | 0.718 | 3.561 | 87.9 | 1.6132 | 24.0 | 666.0 | 20.2 | 354.70 | 7.12 |
| 2 | 0.09604 | 40.0 | 6.41 | 0.0 | 0.447 | 6.854 | 42.8 | 4.2673 | 4.0 | 254.0 | 17.6 | 396.90 | 2.98 |
| 3 | 0.01870 | 85.0 | 4.15 | 0.0 | 0.429 | 6.516 | 27.7 | 8.5353 | 4.0 | 351.0 | 17.9 | 392.43 | 6.36 |
| 4 | 0.52693 | 0.0 | 6.20 | 0.0 | 0.504 | 8.725 | 83.0 | 2.8944 | 8.0 | 307.0 | 17.4 | 382.00 | 4.63 |
这些输入数据特征中的每一个都使用不同的尺度存储。一些特征由0和1之间的比例表示,其他特征的范围在1和12之间,有些是0和100之间的范围,等等。因此需要对数据进行归一化处理。
mean = train_data.mean(axis=0)
std = train_data.std(axis=0)
train_data = (train_data - mean) / std
test_data = (test_data - mean) / std接下来进行模型的构建,定义网络层次。
#模型构建,3个全连接层
def build_model():
model=keras.Sequential([keras.layers.Dense(64,activation=tf.nn.relu,input_shape=(train_data.shape[1],)),
keras.layers.Dense(64,activation=tf.nn.relu),keras.layers.Dense(1)])
optimizer=tf.train.RMSPropOptimizer(0.001)
model.compile(loss="mse",optimizer=optimizer,metrics=['mae'])
return model_________
model=build_model()
model.summary()#打印模型网络结构
________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_16 (Dense) (None, 64) 896
_________________________________________________________________
dense_17 (Dense) (None, 64) 4160
_________________________________________________________________
dense_18 (Dense) (None, 1) 65
=================================================================
Total params: 5,121
Trainable params: 5,121
Non-trainable params: 0#自定义一个回调函数:回调函数是一组在训练的特定阶段被调用的函数集,
#你可以使用回调函数来观察训练过程中网络内部的状态和统计信息。
#通过传递回调函数列表到模型的.fit()中,即可在给定的训练阶段调用该函数集中的函数。
class PrintDot(keras.callbacks.Callback):
def on_epoch_end(self,epoch,logs):
if epoch%100==0:
print('epoch')
print('.',end='')
EPOCHS=500
history=model.fit(train_data,train_label,epochs=EPOCHS,validation_split=0.2,verbose=0,callbacks=[PrintDot()])
print(history.history.keys())接下来展示训练情况:
import matplotlib.pyplot as plt
def plot_history(history):
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Abs ERROR [1000$]')
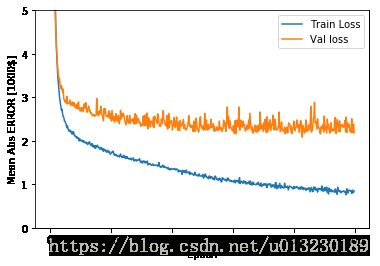
plt.plot(history.epoch,np.array(history.history['mean_absolute_error']),label='Train Loss')
plt.plot(history.epoch,np.array(history.history['val_mean_absolute_error']),label='Val loss')
plt.legend()
plt.ylim([0,5])
plt.show()
plot_history(history)该图显示在大约200个epochs之后模型的改进不大。让我们更新model.fit方法,当验证分数没有提高时自动停止训练。我们将使用回调函数来测试每一个时期的训练条件。如果经过设定的epochs数量后没有显示出改善,则自动停止训练。
model=build_model()
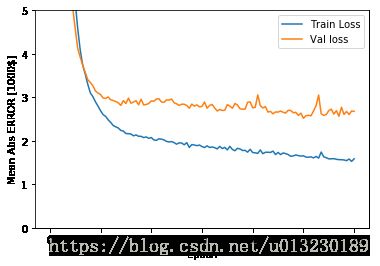
early_stop=keras.callbacks.EarlyStopping(monitor='val_loss',patience=20)
history=model.fit(train_data,train_label,epochs=EPOCHS,validation_split=0.2,verbose=0,callbacks=[early_stop,PrintDot()])
plot_history(history)
[loss,mae]=model.evaluate(test_data,test_label,verbose=0)
print("Testing set Mean Abs Error:${:7.2f}".format(mae*1000))