机器学习实战 EM算法 python3实现

EM算法送上，网络上原理到处都是，一定写的比我好，大家可以来参考一下python3的代码，原理可以看看别的大神的。

 

1.算法原理

EM 算法是 Dempster,Laind,Rubin 于 1977 年提出的求参数极大似然估计的一种方法，它可以从非完整数据集中对参数进行 MLE 估计，是一种非常简单实用的学习算法。这种方法可以广泛地应用于处理缺损数据，截尾数据，带有噪声等所谓的不完全数据。

可以有一些比较形象的比喻说法把这个算法讲清楚。比如说食堂的大师傅炒了一份菜，要等分成两份给两个人吃，显然没有必要拿来天平一点的精确的去称分量，最简单的办法是先随意的把菜分到两个碗中，然后观察是否一样多，把比较多的那一份取出一点放到另一个碗中，这个过程一直迭代地执行下去，直到大家看不出两个碗所容纳的菜有什么分量上的不同为止。

EM算法就是这样，假设我们估计知道A和B两个参数，在开始状态下二者都是未知的，并且知道了A的信息就可以得到B的信息，反过来知道了B也就得到了A。可以考虑首先赋予A某种初值，以此得到B的估计值，然后从B的当前值出发，重新估计A的取值，这个过程一直持续到收敛为止。

在统计学中，最大期望（EM）算法是在概率（probabilistic）模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐藏变量（Latent Variable）。最大期望经常用在机器学习和计算机视觉的数据聚类（Data Clustering）领域。

最大期望算法经过两个步骤交替进行计算  ：

1）计算期望（E），利用概率模型参数的现有估计值，计算隐藏变量的期望；

2）最大化（M），利用E 步上求得的隐藏变量的期望，对参数模型进行最大似然估计。

3）M 步上找到的参数估计值被用于下一个 E 步计算中，这个过程不断交替进行。

总体来说，EM的算法流程如下：

1.初始化分布参数

2.重复直到收敛：

E步骤：估计未知参数的期望值，给出当前的参数估计。

M步骤：重新估计分布参数，以使得数据的似然性最大，给出未知变量的期望估计。

2. 总结

如果将样本看作观察值，潜在类别看作是隐藏变量，那么聚类问题也就是参数估计问题，只不过聚类问题中参数分为隐含类别变量和其他参数，这犹如在x-y坐标系中找一个曲线的极值，然而曲线函数不能直接求导，因此什么梯度下降方法就不适用了。但固定一个变量后，另外一个可以通过求导得到，因此可以使用坐标上升法，一次固定一个变量，对另外的求极值，最后逐步逼近极值。对应到EM上，E步估计隐含变量，M步估计其他参数，交替将极值推向最大。EM中还有“硬”指定和“软”指定的概念，“软”指定看似更为合理，但计算量要大，“硬”指定在某些场合如K-means中更为实用（要是保持一个样本点到其他所有中心的概率，就会很麻烦）。

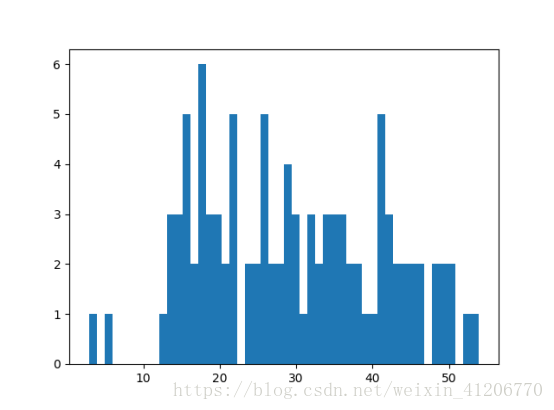
Import  math Import  copy Import  numpy  as  np import  matplotlib.pyplot  as  plt isdebug = False # 指定k个高斯分布参数，这里指定k=2。注意2个高斯分布具有相同均方差Sigma，分别为Mu1,Mu2。 def ini_data(Sigma, Mu1, Mu2, k, N):     global X  # X产生的数据 ,k维向量     global Mu  # 初始均值     global Expectations     X = np.zeros((1, N))     Mu = np.random.random(2)  # 随机产生一个初始均值。     Expectations = np.zeros((N, k))  # k个高斯分布，100个二维向量组成的矩阵。     for i in range(0, N):         if np.random.random(1) > 0.5: # 随机从均值为Mu1,Mu2的分布中取样。             X[0, i] = np.random.normal() * Sigma + Mu1         else:             X[0, i] = np.random.normal() * Sigma + Mu2         if isdebug:             print("***********")     print(u"初始观测数据X：")     print(X) # EM算法：步骤1，计算E[zij] def e_step(Sigma, k, N): # 求期望。sigma协方差，k高斯混合模型数，N数据个数。     global Expectations  # N个k维向量     global Mu     global X     for i in range(0, N):         Denom = 0     for j in range(0, k):         Denom += math.exp((-1 / (2 * (float(Sigma ** 2)))) * (float(X[0, i] - Mu[j])) ** 2) # Denom  分母项  Mu(j)第j个高斯分布的均值。     for j in range(0, k):         Numer = math.exp((-1 / (2 * (float(Sigma ** 2)))) * (float(X[0, i] - Mu[j])) ** 2)  # 分子项     Expectations[i, j] = Numer / Denom  # 期望，计算出每一个高斯分布所占的期望，即该高斯分布以多大比例形成这个样本 # EM算法：步骤2，求最大化E[zij]的参数Mu def m_step(k, N): # 最大化     global Expectations  # 期望值     global X  # 数据     for j in range(0, k): # 遍历k个高斯混合模型数据         Numer = 0  # 分子项         Denom = 0  # 分母项     for i in range(0, N):         Numer += Expectations[i, j] * X[0, i]  # 每一个高斯分布的期望*该样本的值。         Denom += Expectations[i, j]  # 第j个高斯分布的总期望值作为分母         Mu[j] = Numer / Denom  # 第j个高斯分布新的均值， # 算法迭代iter_num次，或达到精度Epsilon停止迭代 def run(Sigma, Mu1, Mu2, k, N, iter_num, Epsilon):     ini_data(Sigma, Mu1, Mu2, k, N)     print(X)     print(u"初始:", Mu)  # 初始均值     for i in range(iter_num):         Old_Mu = copy.deepcopy(Mu)  # 算法之前的MU         e_step(Sigma, k, N)         m_step(k, N)         print(i, Mu)  # 经过EM算法之后的MU，         if sum(abs(Mu - Old_Mu)) < Epsilon:             break if __name__ == '__main__':     run(6, 40, 20, 2, 100, 100, 0.001)     plt.hist(X[0, :], 50)     plt.show()

结果： 初始观测数据X： [[ 34.78479349  40.8762506   12.9259573   17.16456673  16.3469559    14.5410094   25.78720329  17.6779438   35.82670264  41.90071202    50.52081174  26.38782308  21.04963529  14.56343039  38.21448941    49.69993673  48.18442754  44.51268208  26.25675349  40.86309978    44.02344275  41.49166553  21.55141972   5.75166566  34.16528679    19.70743537  30.42653305  39.23467249  40.34117738  23.60869141    28.5130148   17.287984    17.33970054  16.01856562  38.22256625    34.81288304  15.24771646  42.2952032   49.09309169  53.95353144    32.16791165  29.0789197   48.66267963  41.61831626  21.31745232    35.886364    15.29341564  19.08278906  18.612558    50.07119199    31.17027178  34.35832737  19.79392945  37.1648494   13.38859369    15.28348077  21.86257621  28.53368242  18.00679612  29.3180723    19.50236702  42.7221693   32.27174091  13.13910741  14.47212264    29.98649409  46.30665712  32.14165658   2.84063103  25.67421301    32.7497982   42.17391758  33.22993139  52.13921332  35.17490892    45.82663241  41.61183305  20.31732587  15.17501376  22.13357363    45.05877176  45.66095107  33.53623831  17.80499695  27.53976863    24.60028367  27.87441091  18.43420556  30.05336577  16.23903851    13.13443783  43.42828628  21.37174492  27.25854313  37.4277017 ]] [[ 34.78479349  40.8762506   12.9259573   17.16456673  16.3469559    14.5410094   25.78720329  17.6779438   35.82670264  41.90071202    50.52081174  26.38782308  21.04963529  14.56343039  38.21448941    49.69993673  48.18442754  44.51268208  26.25675349  40.86309978    25.95215462  25.69322242  24.25158242  36.06655722  24.90611346    44.02344275  41.49166553  21.55141972   5.75166566  34.16528679    19.70743537  30.42653305  39.23467249  40.34117738  23.60869141    28.5130148   17.287984    17.33970054  16.01856562  38.22256625    34.81288304  15.24771646  42.2952032   49.09309169  53.95353144    32.16791165  29.0789197   48.66267963  41.61831626  21.31745232    35.886364    15.29341564  19.08278906  18.612558    50.07119199    31.17027178  34.35832737  19.79392945  37.1648494   13.38859369    15.28348077  21.86257621  28.53368242  18.00679612  29.3180723    19.50236702  42.7221693   32.27174091  13.13910741  14.47212264    29.98649409  46.30665712  32.14165658   2.84063103  25.67421301    32.7497982   42.17391758  33.22993139  52.13921332  35.17490892    45.82663241  41.61183305  20.31732587  15.17501376  22.13357363    45.05877176  45.66095107  33.53623831  17.80499695  27.53976863    24.60028367  27.87441091  18.43420556  30.05336577  16.23903851    13.13443783  43.42828628  21.37174492  27.25854313  37.4277017 ]] 初始: [ 0.1492249   0.53474567] 0 [  0.1492249  37.4277017] 1 [  0.1492249  37.4277017]