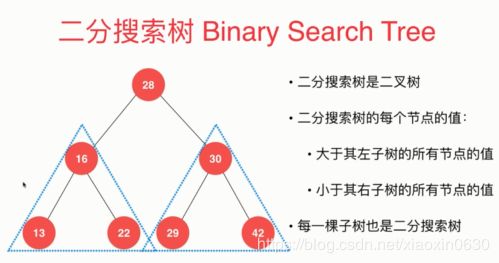
平衡树——旋转的原理、左旋转、右旋转、LR、RL

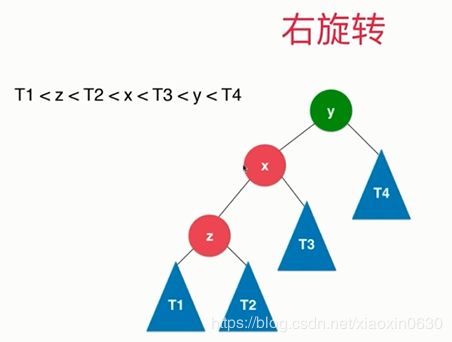
右旋转

我把以前的二分树的图片模拟、和这张的旋转相对应

T1

二分树就是左边的都小于的右边的，上面的T1小于T4 从小到大

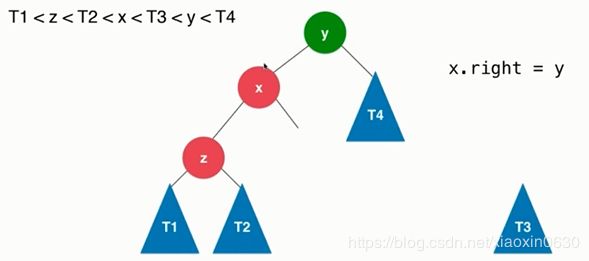
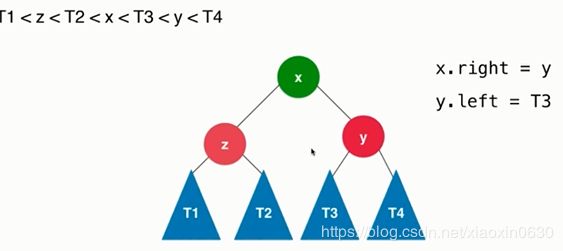
然后先把T3放在一边，再把y移到x的右边，再把T3放在y的左边

得到代码

x.right=y 

x.left=T3

最后就是这样

更新高度

 

然后就是代码

这是旋转右代码

    // 对节点y进行向右旋转操作，返回旋转后新的根节点x
    //        y                              x
    //       / \                           /   \
    //      x   T4     向右旋转 (y)        z     y
    //     / \       - - - - - - - ->    / \   / \
    //    z   T3                       T1  T2 T3 T4
    //   / \
    // T1   T2
    private Node rightRotate(Node y) {
        Node x = y.left;
        Node T3 = x.right;

        // 向右旋转过程
        x.right = y;
        y.left = T3;

        // 更新height
        y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
        x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

        return x;
    }

平衡维护

        if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0)//如果左节点的平衡大于1 那么就右选择
            return rightRotate(node);

    // 向以node为根的二分搜索树中插入元素(key, value)，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, K key, V value){

        if(node == null){
            size ++;
            return new Node(key, value);
        }

        if(key.compareTo(node.key) < 0)
            node.left = add(node.left, key, value);
        else if(key.compareTo(node.key) > 0)
            node.right = add(node.right, key, value);
        else // key.compareTo(node.key) == 0
            node.value = value;

        // 更新height
        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));

        // 计算平衡因子
        int balanceFactor = getBalanceFactor(node);
//        if(Math.abs(balanceFactor) > 1)
//            System.out.println("unbalanced : " + balanceFactor);

        // 平衡维护
        if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0)
            return rightRotate(node);

        if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0)
            return leftRotate(node);

        return node;
    }

 

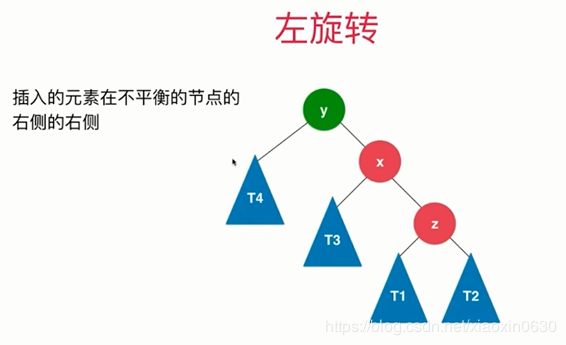
左旋转

左旋转和右旋转思路一样的，就是旋转方向不一样，判断因子也不一样

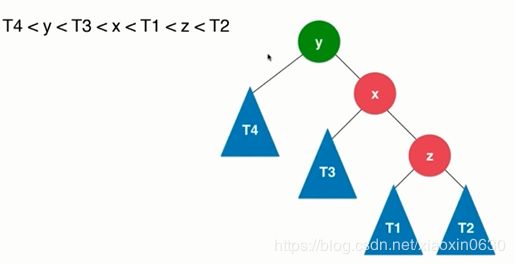
公式 T4

 

把x左节点放在一边，也就是T3

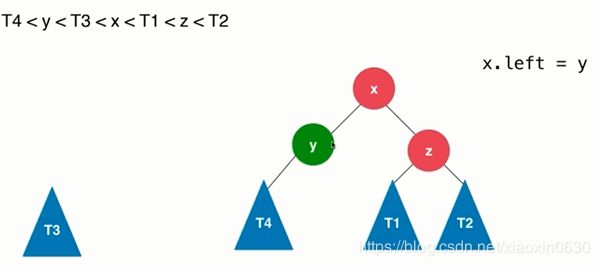
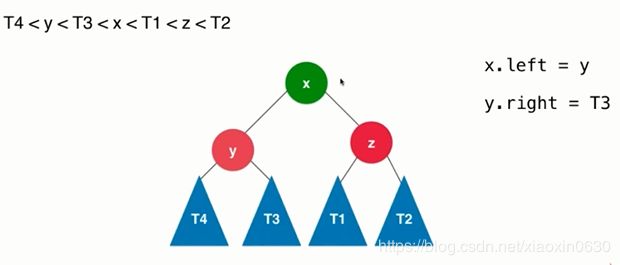
x.left=y

y.right=T3

 

代码其实和右旋转差不多

 

 

左旋转代码

    // 对节点y进行向左旋转操作，返回旋转后新的根节点x
    //    y                             x
    //  /  \                          /   \
    // T1   x      向左旋转 (y)       y     z
    //     / \   - - - - - - - ->   / \   / \
    //   T2  z                     T1 T2 T3 T4
    //      / \
    //     T3 T4
    private Node leftRotate(Node y) {
        Node x = y.right;
        Node T2 = x.left;

        // 向左旋转过程
        x.left = y;
        y.right = T2;

        // 更新height
        y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
        x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

        return x;
    }

 

    // 向以node为根的二分搜索树中插入元素(key, value)，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, K key, V value){

        if(node == null){
            size ++;
            return new Node(key, value);
        }

        if(key.compareTo(node.key) < 0)
            node.left = add(node.left, key, value);
        else if(key.compareTo(node.key) > 0)
            node.right = add(node.right, key, value);
        else // key.compareTo(node.key) == 0
            node.value = value;

        // 更新height
        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));

        // 计算平衡因子
        int balanceFactor = getBalanceFactor(node);
//        if(Math.abs(balanceFactor) > 1)
//            System.out.println("unbalanced : " + balanceFactor);

        // 平衡维护
        if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0)
            return rightRotate(node);

        if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0)
            return leftRotate(node);

        return node;
    }

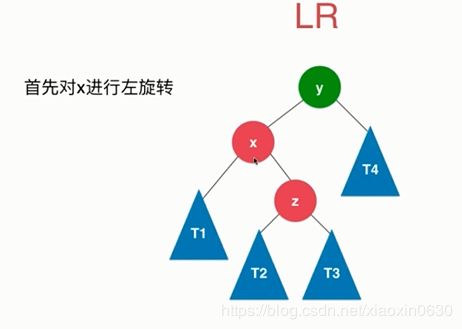
LR RL

这些单纯的旋转都是LL 和RR

但是下面这些是两次选择 LR和RL

LR和RL都要旋转两次

这就是两个状态的代码
        //LR
        if(balanceFactor < -1 && getBalanceFactor(node.left) > 0){
            node.right=rightRotate(node.left);
            return rightRotate(node);
        }
        
        //RL
        if(balanceFactor < -1 && getBalanceFactor(node.right) > 0){
            node.right=rightRotate(node.right);
            return leftRotate(node);
        }

 

 

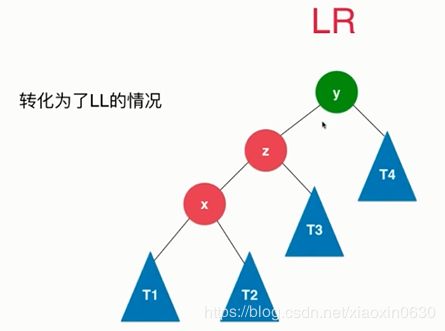
首先左旋转，就变为了LL的情况，在LL的方法就行

转为了LL的情况

 

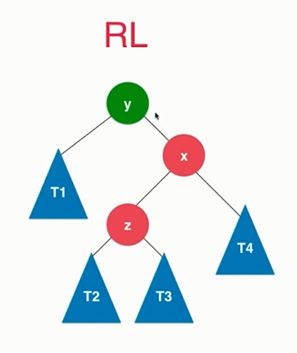
RL

和左旋转差不多，都是一样的思路，右旋转，在根据右旋转的情况

、

 

 

代码如下
        //LR
        if(balanceFactor < -1 && getBalanceFactor(node.left) > 0){
            node.right=rightRotate(node.left);
            return rightRotate(node);
        }
        
        //RL
        if(balanceFactor < -1 && getBalanceFactor(node.right) > 0){
            node.right=rightRotate(node.right);
            return leftRotate(node);
        }

// 向以node为根的二分搜索树中插入元素(key, value)，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, K key, V value){

        if(node == null){
            size ++;
            return new Node(key, value);
        }

        if(key.compareTo(node.key) < 0)
            node.left = add(node.left, key, value);
        else if(key.compareTo(node.key) > 0)
            node.right = add(node.right, key, value);
        else // key.compareTo(node.key) == 0
            node.value = value;

        // 更新height
        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));

        // 计算平衡因子
        int balanceFactor = getBalanceFactor(node);
        if(Math.abs(balanceFactor) > 1)
            System.out.println("unbalanced : " + balanceFactor);

        //平衡维护
        if(balanceFactor >1 && getBalanceFactor(node.left) >=0)//右旋转
        	return rightRotate(node);
        
        if(balanceFactor <-1 && getBalanceFactor(node.right) <=0)//左旋转
        	return leftRotate(node);
        
        
        //LR 
        if(balanceFactor < -1 && getBalanceFactor(node.left) > 0){
        	node.right=rightRotate(node.left);
        	return rightRotate(node);
        }
        
        //RL
        if(balanceFactor < -1 && getBalanceFactor(node.right) > 0){
        	node.right=rightRotate(node.right);
        	return leftRotate(node);
        }
        
        return node;
    }

 

 

删除就添加那些平衡代码

 

private Node remove(Node node, K key){

        if( node == null )
            return null;

        Node retNode;
        if( key.compareTo(node.key) < 0 ){
            node.left = remove(node.left , key);
            // return node;
            retNode = node;
        }
        else if(key.compareTo(node.key) > 0 ){
            node.right = remove(node.right, key);
            // return node;
            retNode = node;
        }
        else{   // key.compareTo(node.key) == 0

            // 待删除节点左子树为空的情况
            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size --;
                // return rightNode;
                retNode = rightNode;
            }

            // 待删除节点右子树为空的情况
            else if(node.right == null){
                Node leftNode = node.left;
                node.left = null;
                size --;
                // return leftNode;
                retNode = leftNode;
            }

            // 待删除节点左右子树均不为空的情况
            else{
                // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
                // 用这个节点顶替待删除节点的位置
                Node successor = minimum(node.right);
                //successor.right = removeMin(node.right);
                successor.right = remove(node.right, successor.key);
                successor.left = node.left;

                node.left = node.right = null;

                // return successor;
                retNode = successor;
            }
        }

        if(retNode == null)
            return null;

        // 更新height
        retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));

        // 计算平衡因子
        int balanceFactor = getBalanceFactor(retNode);

        // 平衡维护
        // LL
        if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0)
            return rightRotate(retNode);

        // RR
        if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0)
            return leftRotate(retNode);

        // LR
        if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
            retNode.left = leftRotate(retNode.left);
            return rightRotate(retNode);
        }

        // RL
        if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
            retNode.right = rightRotate(retNode.right);
            return leftRotate(retNode);
        }

        return retNode;
    }