Meta-learning（元学习）和 3D-CNN 总结

Meta-learning and 3D-CNN 总结

##Meta-learning

**Meta-learning（元学习）**方法是近期的研究热点，加州伯克利大学在这方面做了大量工作。这周阅读了相关论文，总结一下自己的知识。
论文题目：
1.Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks ；
2.One-Shot Visual Imitation Learning via Meta-Learning。

Model-Agnostic Meta-learning 算法提出的初衷是因为目前深度学习所需要的样本量大，而且学习速度慢，在某一个特定的任务训练好参数以后，面对一个新的任务，即使这个任务跟之前的任务具有相关性，但它的鲁棒性也不好，需要重新训练。特别是在应用到机器人模仿学习时（目前自己的研究方向），需要在不同的场景下执行新的任务，但这些任务很多是具有相关性的。所以伯克利分校提出了这样一种算法：通过少量的任务集样本去训练好网络，然后在面对一个新的任务时，能够很快的训练好参数，完成学习过程。这个过程就像人类面对新的任务时，也是由之前的经验来应对新的场景，具有先验知识。

算法核心思想，如下图所示：

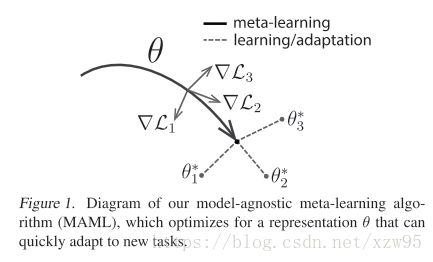
算法个人理解：
1.这是属于监督学习的范围，通过梯度下降来更新参数θ；任务集Ti, fθ表示输入x到输出a的映射；
2.这个算法由两个循环构成，内循环的流程是对任务集中每一个任务Ti，使用训练样本更新参数θ，所以会有i个θ；
3.外循环的流程是将每一个训练好的θ，一共有i个，使用每个任务的测试数据，进行综合更新，损失函数是将每个任务的损失函数累加起来。得到一个新的θ。
4.可以通过形象的比喻就是：你的人生在某一个条件或场景下，你的选择有一个最优的选择，往往人生有时候需要面对不同的场合，要综合考虑很多限制条件，你只能选择一条最适中的路，但是在面对新的机遇时，你不要重头开始，总能很快的到达目的地。

这个算法因为是无特定模型的，所以可以应用到很多算法上面，如监督回归，增强学习等。应用到不同方法时只是损失函数不同，核心思想不变。

元学习的算法思想总结到这里，论文中有具体实验结果，可以到文中细读。

##3D CNN介绍

因为需要通过demo来进行模仿学习，提取视频中的特征，所以也总结一下3D CNN 的算法。参考论文题目：3D Convolutional Neural Networks for Human Action Recognition。

采用2D CNN对视频进行操作的方式，一般都是对视频的每一帧图像分别利用CNN来进行识别，这种方式的识别没有考虑到时间维度的帧间运动信息。下面是传统的2DCNN对图像进行采用2D卷积核进行卷积操作：

使用3D CNN能更好的捕获视频中的时间和空间的特征信息，以下是3D CNN对图像序列（视频）采用3D卷积核进行卷积操作：

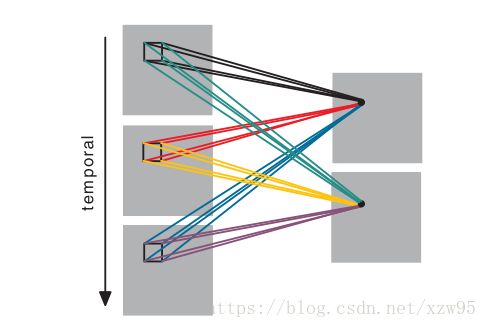
对连续的三帧图像进行卷积操作，这样卷积层中的每一个特征将与多个相邻的连续帧相连，注意：卷积核提取特征时可以采用多种卷积核，每个权值不同，提取多种特征；也可以使用一个卷积核，共享权值。
##3D CNN 结构

输入层（input）：连续的大小为60*40的视频帧图像作为输入。
硬线层（hardwired，H1）：每帧提取5个通道信息（灰度gray，横坐标梯度（gradient-x），纵坐标梯度（gradient-y），x光流（optflow-x），y光流（optflow-y））。前面三个通道的信息可以直接对每帧分别操作获取，后面的光流（x，y）则需要利用两帧的信息才能提取，因此

H1层的特征maps数量：（7+7+7+6+6=33），特征maps的大小依然是60* 40；

卷积层（convolution C2）：以硬线层的输出作为该层的输入，对输入5个通道信息分别使用大小为7* 7 * 3的3D卷积核进行卷积操作（7* 7表示空间维度，3表示时间维度，也就是每次操作3帧图像），同时，为了增加特征maps的个数，在这一层采用了两种不同的3D卷积核，因此C2层的特征maps数量为：
（（（7-3）+1）* 3+（（6-3）+1）* 2）* 2=23* 2
这里右乘的2表示两种卷积核。
特征maps的大小为：（（60-7）+1）* （（40-7）+1）=54 * 34

降采样层（sub-sampling S3）：在该层采用max pooling操作，降采样之后的特征maps数量保持不变，因此S3层的特征maps数量为：23 *2

特征maps的大小为：（（54 / 2） * （34 /2）=27 *17

卷积层（convolution C4）：对两组特征maps分别采用7 6 3的卷积核进行操作，同样为了增加特征maps的数量，文中采用了三种不同的卷积核分别对两组特征map进行卷积操作。这里的特征maps的数量计算有点复杂，请仔细看清楚了

我们知道，从输入的7帧图像获得了5个通道的信息，因此结合总图S3的上面一组特征maps的数量为（（7-3）+1） * 3+（（6-3）+1） * 2=23,可以获得各个通道在S3层的数量分布：

前面的乘3表示gray通道maps数量= gradient-x通道maps数量= gradient-y通道maps数量=（7-3）+1）=5；

后面的乘2表示optflow-x通道maps数量=optflow-y通道maps数量=（6-3）+1=4；

假设对总图S3的上面一组特征maps采用一种7 6 3的3D卷积核进行卷积就可以获得：

（（5-3）+1）* 3+（（4-3）+1）* 2=9+4=13；

三种不同的3D卷积核就可获得13* 3个特征maps，同理对总图S3的下面一组特征maps采用三种不同的卷积核进行卷积操作也可以获得13*3个特征maps，

因此C4层的特征maps数量：13* 3* 2=13* 6

C4层的特征maps的大小为：（（27-7）+1）* （（17-6）+1）=21*12

降采样层（sub-sampling S5）：对每个特征maps采用3 3的核进行降采样操作，此时每个maps的大小：7* 4

在这个阶段，每个通道的特征maps已经很小，通道maps数量分布情况如下：

gray通道maps数量= gradient-x通道maps数量= gradient-y通道maps数量=3

optflow-x通道maps数量=optflow-y通道maps数量=2；

卷积层（convolution C6）：此时对每个特征maps采用7* 4的2D卷积核进行卷积操作，此时每个特征maps的大小为：1*1，至于数量为128是咋来的，就不咋清楚了，估计是经验值。

对于CNNs，有一个通用的设计规则就是：在后面的层（离输出层近的）特征map的个数应该增加，这样就可以从低级的特征maps组合产生更多类型的特征。

通过多层的卷积和降采样，每连续7帧图像就可以获得128维的特征向量。输出层的单元数与视频动作数是相同的，输出层的每个单元与这128维的特征向量采用全连接。在后面一般采用线性分类器对128维的特征向量进行分类，实现行为识别，3DCNN模型中所有可训练的参数都是随机初始化的，然后通过在线BP算法进行训练。

下面是3DCNN各通道数量变化情况以及特征maps大小变化情况：

3D CNN参考了博文：3D CNN框架结构各层计算。
不得任意转载，如有需要注明出处。

---