关联分析（三）--GSP算法

转自：http://www.cnblogs.com/liuqing910/p/8964863.html

关联规则--Apriori算法部分讨论的关联模式概念都强调同时出现关系，而忽略数据中的序列信息（时间/空间）：

时间序列：顾客购买产品X，很可能在一段时间内购买产品Y；

空间序列：在某个点发现了现象A，很可能在下一个点发现现象Y。

例：6个月以前购买奔腾PC的客户很可能在一个月内订购新的CPU芯片。

注：1）序列模型=关联规则+时间/空间维度

       2）这里讨论的序列模式挖掘指的是时间维度上的挖掘。

一、基本定义

序列：将与对象A有关的所有事件按时间戳增序排列，就得到对象A的一个序列s。

元素（事务）：序列是事务的有序列表，可记作，其中每个是一个或多个事件（项）的集族，即。

序列的长度：序列中元素的个数。

序列的大小：序列中事件的个数，K-序列是包含k个事件的序列。

如：如下课程序列中包含4个元素，8个事件。

子序列：序列t是另一个序列s的子序列，若t中每个有序元素都是s中一个有序元素的子集。即，序列是序列的子序列，若存在整数，使得。

例：

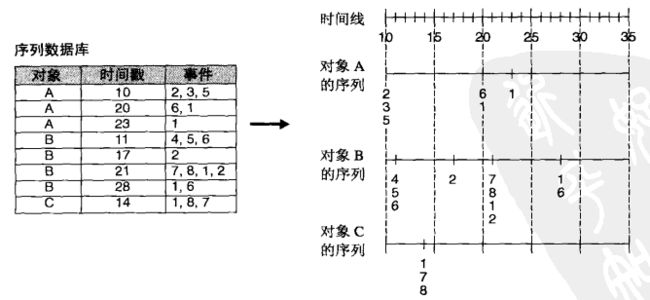
序列数据库：包含一个或多个序列数据的数据集，如下：

 

二、序列模式挖掘

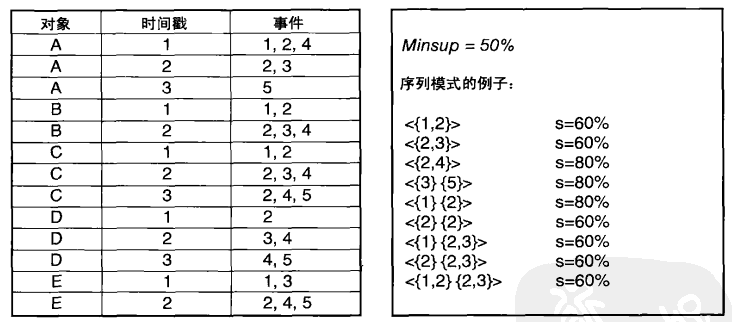
序列的支持度：序列s的支持度指包含s的所有数据序列（与单个数据对象（上例中的A/B/C）相关联的事件的有序列表）所占的比例，若序列s的支持度大于或等于minsup，则称s是一个序列模式（频繁序列）。

序列模式挖掘：给定序列数据集D和用户指定的最小支持度minsup，找出支持度大于或等于minsup的所有序列。

例：下例中，假设minsup=50%，因为序列（子序列）<{2} {2，3}>包含在A,B,C中，所以其支持度=3/5=0.6，其他类似。

 

 

产生序列模式

1、蛮力法

枚举所有可能的序列，并统计它们各自的支持度。值得注意的是：候选序列的个数比候选项集的个数大得多，两个原因如下：

 

2、类Apriori算法

候选过程：一对频繁（k-1）序列合并，产生候选k-序列。为不重复产生，合并原则如下：

序列S1与序列S2合并，仅当从S1中去掉第一个事件得到的子序列与从S2中去掉最后一个事件得到的子序列相同，合并结果为S1与S2最后一个事件的连接，连接方式有两种：

1）若S2的最后两个事件属于相同的元素，则S2的最后一个事件在合并后的序列中是S1的最后一个元素的一部分；

2）若S2的最后两个事件属于不同的元素，则S2的最后一个事件在合并后的序列中成为连接到S1的尾部的单独元素。

例：

 <(1) (2) (3)> + <(2) (3) (4)> = <(1) (2) (3) (4)> ：除去S1中第一个事件(1)与除去S2中最后一个事件(4)所剩下的子序列均为<(2) (3)>，且S2最后两个事件(3)(4)属于不同的元素，故单独列出；

<(2 5) (3)> + <(5) (3 4)> = <(2 5) (3 4)>：除去事件2和事件4，剩下子序列相同，由于S2最后两个事件(3 4)属于相同的元素，所以合并到S1最后，而不是写成<(2 5) (3) (3 4)>。

 

 

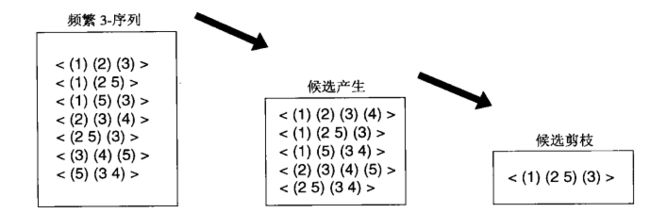
候选剪枝：若候选k-序列的（k-1）-序列至少有一个是非频繁的，则被剪枝。

上例中，候选剪枝后只剩下<{1} {2,5} {3}>。

3、时限约束

施加时限约束时，序列模式的每个元素都与一个时间窗口[l,u]相关联，其中l是该时间窗口内事件的最早发生时间，u是该时间窗口内事件的最晚发生时间。

最大跨度约束：整个序列中所允许的事件的最晚和最早发生时间的最大时间差，记为maxspan，一般地，maxspan越长，在数据序列中检测到模式的可能性越大，但较长的maxspan也可能捕获不真实的模式。

注：最大跨度影响序列模式发现算法的支持度计数，施加最大时间跨度约束之后，有些数据序列就不再支持候选模式。

最小间隔和最大间隔约束：假设最大间隔maxgap=3（天），最小间隔mingap=1，即元素中的事件必须在前一个元素的事件出现后三（一）天内出现。

注：使用最大间隔约束可能违反先验原理，以图2.1为例，无约束情形下，<{2} {5}>和<{2}{3}{5}>的支持度都是60%，若施加约束mingap=0，maxgap=1，<{2} {5}>的支持度下降至40%（缺少D的支持），而<{2}{3}{5}>的支持度仍是60%，即超集的支持度比原集要高——与先验原理违背。使用邻接子序列的概念可避免这一问题。

 

例：

使用邻接子序列修改先验原理如下：

修订的先验原理：若一个k-序列是频繁的，则它的所有邻接（k-1）-子序列也一定是频繁的。

注：根据上述原理，在候选剪枝阶段，并非所有k-1-序列都序列都需要检查（违反最大间隔约束）。

例：若maxgap=1，则不必检查<{1}{2,3}{4}{5}>的子序列<{1}{2,3}{5}>是否频繁，因为{2,3}和{5}之间的时间差为2，大于一个单位，只需考察其邻接子序列：<{1}{2,3}{4}>，<{2,3}{4}{5}>，<1}{2}{4}{5}>，<{1}{3}{4}{5}>。

窗口大小约束：元素中的事件不必同时出现，可定义一个窗口大小阈值（ws）来指定序列模式的任意元素中事件最晚和最早出现之间的最大允许时间差。（ws=0表示同一元素中的所有事件必须同时出现）。

  

--GSP算法

算法基本思路：

1、长度为1的序列模式L1，作为初始的种子集；

2、根据长度为i的种子集Li，通过连接操作和剪切操作生成长度为i+1的候选序列模式，然后扫描数据库，计算每个候选序列模式的支持度，产生长度为i+1的序列模式并作为新的种子集。

3、重复第二步，直到没有新的序列模式或新的候选序列模式产生为止。

解决两大问题：

1、候选集产生：合并+剪枝=期望尽可能少的候选集；

2、支持度计数

两个技巧：

1）哈希树存储数据，减少对于候选序列需要检查的原数据序列个数。

2）改变原数据系列的表达形式以有效发现一个候选项是否是数据序列的子序列。

3、具体做法：

对事物数据库中的每个数据序列的每一项进行哈希，从而确定应该考察哈希树哪些叶子节点中的候选K序列；对于叶子节点中的每个候选K序列，须考察其是否包含在该数据序列中，对每个包含在该数据序列中的候选序列，其计数值加1。

如何考察数据序列d是否包含某个候选K序列s？分两步：

 

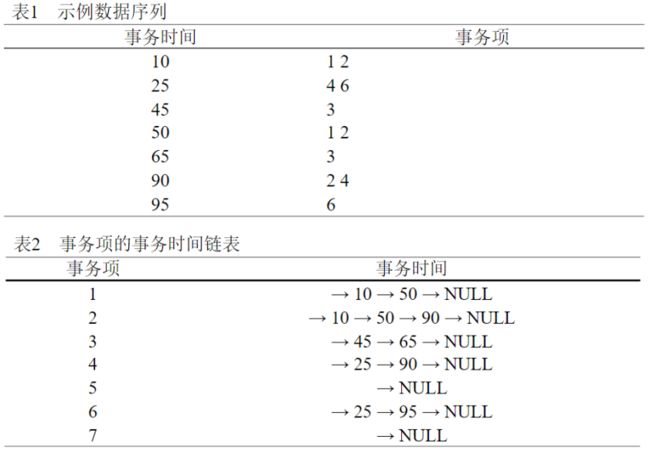
例：假设maxgap=30，mingap=5，ws=0，考察候选序列s=<(1,2)(3)(4)>是否包含在下列数据序列中。

1）首先寻找s的第一个元素（1，2）在该数据序列中第一次出现的位置，对应时间为10；

2）由mingap=5，故在时间15后寻找下一元素（3），发现其第一次出现时间为45，而45-10>30，转入向后阶段；

3）重新寻找（1，2）的第一次出现位置：50，接着在时间55后寻找（3）：65，由65-50<30，故满足最大时间间隔约束，转入向前阶段；

4）寻找（3）的下一个元素（4）在时间70（65+5）后的第一次出现位置：90，由90-65<30，满足；

5）考察结束，包含。