二叉排序树（折半查找树）模板类实现

折半查找树也叫做二叉排序树。所谓的折半查找树就是左子树的所有节点都比跟节点小，右子树的所有节点都比根节点大（不考虑有重复元素的情况）。

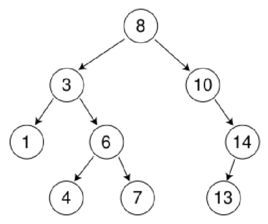
上图就是一颗典型的排序二叉树。它是平衡排序二叉树（AVL）的基础。

可以很容易的看出来，上图的dfs序就是从小到大排好序的。

以下内容来自数据结构与STL。

BinSearchTree类的字段如下：

#ifndef _BIN_SEARCH_TREE_
#define _BIN_SEARCH_TREE_
template
class BinSearchTree {
	struct tree_node {
		T item;
		tree_node *parent, *left, *right;
		bool isHeader;
	};
	tree_node *header;
	unsigned node_count;
};
#endif

节点tree_node中包含了一个数据字段（item），三个指针字段，一个头结点字段（采用头结点形式实现）

BinSearchTree中包含一个指向头结点的指针header，跟一个记录节点个数的node_count字段。

构造器：

BinSearchTree(){ 
		header = new tree_node; 
		header->parent = NULL;//parent指向根节点，在一颗空树中指定根节点是不合理的
		header->left = header;
		header->right = header;
		header->isHeader = true;
		node_count = 0;
	}

在BinSearchTree中添加一个迭代器类Iterator。

#ifndef _BIN_SEARCH_TREE_
#define _BIN_SEARCH_TREE_
template
class BinSearchTree {
	struct tree_node {
		T item;
		tree_node *parent, *left, *right;
		bool isHeader;
	};
	typedef tree_node *Link;
	tree_node *header;
	unsigned node_count;
protected:
	class Iterator {
	protected:
		Link link;
	public:
		Iterator() {}
		Iterator(Link new_link) :link(new_link) {}
	};
public:
	BinSearchTree(){ 
		header = new tree_node; 
		header->parent = NULL;//parent指向根节点，在一颗空树中指定根节点是不合理的
		header->left = header;
		header->right = header;
		header->isHeader = true;
		node_count = 0;
	}
};
#endif

向BinSearchTree类中添加size方法：

unsigned size() {
		return node_count;
	}

下面分别添加find，insert，erase方法。

Iterator find(const T& item) {
		Link parent = header;
		Link child = header->parent;
		while (child != NULL) {
			if (!(child->item < item)) {
				parent = child;
				child = child->left;
			}
			else child = child->right;
		}
		if (parent == header || item < parent->item)return end();
		return parent;
	}

这个方法寻找折半查找树中是否有item项。有则返回它的迭代器，没有返回end()//最大值的下一个。这段代码可以仔细考虑考虑。

这段代码优美的地方在于通过每次查找都要到达树叶节点来减少while循环里头判断语句。

根节点的祖先是头结点，child起初指向根节点，parent指向头结点。然后开始判断。

看下结束条件parent==header这个，什么条件会出现呢？parent更新是出现在item不属于右子树的时候将会被更新，所以parent==header指的是若item比所有的节点都大的时候。

若item属于右子树，新的问题跟原问题是不是很相同，item可能出现在新树的左子树或者右子树上，只是范围缩小了。若item不属于右子树，那么它可能是（1）子树的根节点或者是（2）这颗子树的左子树。简单讨论假设没有相同的项。1条件下那么左子树中没有比他更大了，就是说下面不可能存在item<=child->item的情况了，parent不会被更新，到最后也是item==parent->item这样。2条件的话，跟item属于右子树的情况是一样的。

insert方法有两种情况，一种是树空的情况，一种是树不空的情况。

Iterator Insert(const T& item) {
		if (header->parent == NULL) {
			insertLeaf(item, header, header->parent);
			header->left = header->parent;
			header->right = header->parent;
			return header->parent;
		}
		else {
			Link parent = header,
				child = header->parent;
			while (child != NULL) {
				parent = child;
				if (item < child->item) child = child->left;
				else child = child->right;
			}
			if (item < parent->item) {
				insertLeaf(item, parent, parent->left);
				if (header->left == parent)return header->left = parent->left;
			}
			else {
				insertLeaf(item, parent, parent->right);
				if (header->right == parent)return header->right = parent->right;
			}
		}
	}

这段代码还是比较好理解的。insertLeaf函数代码：

void insertLeaf(const T&item, Link& parent, Link& child) {
		child = new tree_node;
		child->item = item;
		child->parent = parent;
		child->left = child->right = NULL;
		child->isHeader = false;
		node_count++;
	}

这个函数应该是不对外公开的，应该放在private中。

递归版本的代码比较短，但是能迭代尽量迭代吧。

现在考虑最难的erase方法，主要是分类太多，AVL中的erase方法也一样麻烦。

原型：void erase(Iterator itr);

主要的思路就是删除了该节点用直接后继来替代它。

deleteLink（LInk& link);//删除link指向的节点。

prune(Link &link);//当节点只有左子树或者右子树的时候删除该节点。

void erase(const Iterator& itr) {//其实本人也不知道这下面是干嘛用的，求路过的高人指点
		if (itr.link->parent->parent == itr.link)//根节点的父亲是头结点，头结点的父亲是根节点。
			deleteLink(itr.link->parent->parent);//deleteLink(itr.link);
		else if (itr.link->parent->left == itr.link)deleteLink(itr.link->parent->left);
		else deleteLink(itr.link->parent->right);
	}

上面的代码个人感觉是废话。重点讨论下面的deleteLink

void deleteLink(Link& link) {
		if (link->left == NULL || link->right == NULL) {
			prune(link);
		}
		else if (link->right->left == NULL) {
			link->item = link->right->item;
			prune(link->right);
		}
		else {
			Link temp = link->right->left;
			while (temp->left != NULL)temp = temp->left;
			link->item = temp->item;
			prune(temp);
		}
	}

要删除的节点是link指向的，当link没有左子树或者没有右子树时直接调用prune即可。

如果左右子树都存在时，就要找到它的直接后继了，直接后继是右子树的最左下角。

下面是prune函数。记得prune的前置条件是link指向的节点不存在左右子树都存在的情况。

void prune(Link &link) {
		Link linkCopy = link,
						newLink;
		node_count--;
		if ((link->left == NULL) && (link->right == NULL)) {
			if (link == header->left) header->left = link->parent;
			if (link == header->right)header->right = link->parent;
			link = NULL;
		}
		else if (link->left == NULL) {
			link = link->right;
			link->parent = linkCopy->parent;
			if (linkCopy == header->left) {
				newLink = link;
				while ((newLink->left) != NULL) {
					newLink = newLink->left;
				}
				header->left = newLink;
			}
		}
		else {
			link = link->left;
			link->parent = linkCopy->parent;
			if (linkCopy == header->parent) {
				newLink = link;
				while ((newLink->right) != NULL) {
					newLink = newLink->right;
				}
				header->right = newLink;
			}
		}
		delete linkCopy;
	}

prune的主要工作就是调整header的left跟right。

析构函数：

void destroy(Link link) {
		if (link != NULL) {
			destroy(link->left);
			destroy(link->right);
			delete(link);
		}
	}
	~BinSearchTree() {
		destroy(header->parent);
	}

采用后序遍历，想想为啥。

完整代码（没有包括迭代器类的实现）

#pragma once
#ifndef _BIN_SEARCH_TREE_
#define _BIN_SEARCH_TREE_
template
class BinSearchTree {
	struct tree_node {
		T item;
		tree_node *parent, *left, *right;
		bool isHeader;
	};
	typedef tree_node *Link;
	tree_node *header;
	unsigned node_count;
	void insertLeaf(const T&item, Link& parent, Link& child) {
		child = new tree_node;
		child->item = item;
		child->parent = parent;
		child->left = child->right = NULL;
		child->isHeader = false;
		node_count++;
	}
public:
	class Iterator {
	public:
		Link link;
	public:
		Iterator() {}
		Iterator(Link new_link) :link(new_link) {}
		bool operator==(const Iterator& itr) {
			if (link == itr.link)return true;
			return false;
		}
	};
	BinSearchTree(){ 
		header = new tree_node; 
		header->parent = NULL;//parent指向根节点，在一颗空树中指定根节点是不合理的
		header->left = header;
		header->right = header;
		header->isHeader = true;
		node_count = 0;
	}
	unsigned size() {
		return node_count;
	}
	Iterator end() {
		return Iterator(header);
	}
	Iterator find(const T& item) {
		Link parent = header;
		Link child = header->parent;
		while (child != NULL) {
			if (!(child->item < item)) {
				parent = child;
				child = child->left;
			}
			else child = child->right;
		}
		if (parent == header || item < parent->item)return end();
		return parent;
	}
	Iterator Insert(const T& item) {
		if (header->parent == NULL) {
			insertLeaf(item, header, header->parent);
			header->left = header->parent;
			header->right = header->parent;
			return header->parent;
		}
		else {
			Link parent = header,
				child = header->parent;
			while (child != NULL) {
				parent = child;
				if (item < child->item) child = child->left;
				else child = child->right;
			}
			if (item < parent->item) {
				insertLeaf(item, parent, parent->left);
				if (header->left == parent)return header->left = parent->left;
			}
			else {
				insertLeaf(item, parent, parent->right);
				if (header->right == parent)return header->right = parent->right;
			}
		}
	}
	void prune(Link &link) {
		Link linkCopy = link,
						newLink;
		node_count--;
		if ((link->left == NULL) && (link->right == NULL)) {
			if (link == header->left) header->left = link->parent;
			if (link == header->right)header->right = link->parent;
			link = NULL;
		}
		else if (link->left == NULL) {
			link = link->right;
			link->parent = linkCopy->parent;
			if (linkCopy == header->left) {
				newLink = link;
				while ((newLink->left) != NULL) {
					newLink = newLink->left;
				}
				header->left = newLink;
			}
		}
		else {
			link = link->left;
			link->parent = linkCopy->parent;
			if (linkCopy == header->parent) {
				newLink = link;
				while ((newLink->right) != NULL) {
					newLink = newLink->right;
				}
				header->right = newLink;
			}
		}
		delete linkCopy;
	}
	void deleteLink(Link& link) {
		if (link->left == NULL || link->right == NULL) {
			prune(link);
		}
		else if (link->right->left == NULL) {
			link->item = link->right->item;
			prune(link->right);
		}
		else {
			Link temp = link->right->left;
			while (temp->left != NULL)temp = temp->left;
			link->item = temp->item;
			prune(temp);
		}
	}
	void erase(const Iterator& itr) {//其实本人也不知道这下面是干嘛用的，求路过的高人指点
		if (itr.link->parent->parent == itr.link)//根节点的父亲是头结点，头结点的父亲是根节点。
			deleteLink(itr.link->parent->parent);//deleteLink(itr.link);
		else if (itr.link->parent->left == itr.link)deleteLink(itr.link->parent->left);
		else deleteLink(itr.link->parent->right);
	}
	void destroy(Link link) {
		if (link != NULL) {
			destroy(link->left);
			destroy(link->right);
			delete(link);
		}
	}
	~BinSearchTree() {
		destroy(header->parent);
	}
};
#endif

模板类的定义跟原型不要分开，不然会出现错误的。