求最大公约数的4种常用算法
一、问题描述:
运行最大公约数的常用算法
二、问题分析与设计:
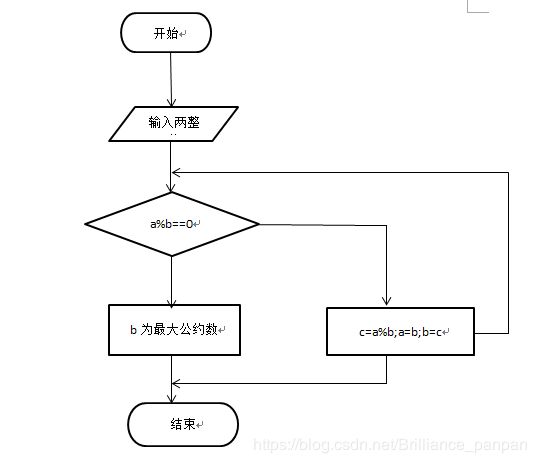
1.辗转相除法(又名欧几里德法)
①函数嵌套调用
其算法过程为: 前提:设两数为a,b设其中a 做被除数,b做除数,temp为余数
1、大数放a中、小数放b中;
2、求a/b的余数;
3、若temp=0则b为最大公约数;
4、如果temp!=0则把b的值给a、temp的值给a;
5、返回第二步;
代码:
#include测试及测试代码与平均运行时间:
测试代码:
#include②函数递归调用
#include测试及测试代码与平均运行时间:
测试代码:
#include穷举法求两个正整数的最大公约数的解题步骤:从两个数中较小数开始由大到小列举,直到找到公约数立即中断列举,得到的公约数便是最大公约数。
定义1:对两个正整数a,b如果能在区间[a,0]或[b,0]内能找到一个整数temp能同时被a和b所整除,则temp即为最大公约数。
定义2:对两个正整数a,b,如果若干个a之和或b之和能被b所整除或能被a所整除,则该和数即为所求的最小公倍数。
代码:
#include测试及测试代码与平均运行时间:
测试代码:
#include更相减损术,是出自《九章算术》的一种求最大公约数的算法,它原本是为约分而设计的,但它适用于任何需要求最大公约数的场合。《九章算术》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数,即“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。以等数约之。”
翻译成现代语言如下:
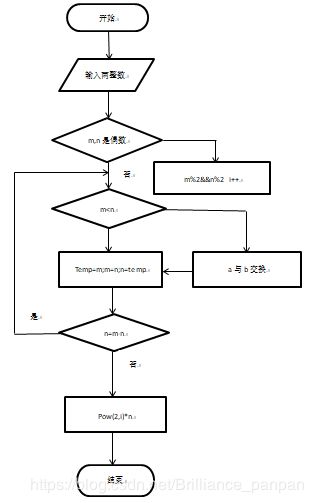
第一步:任意给定两个正整数;判断它们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止。
则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。
其中所说的“等数”,就是最大公约数。求“等数”的办法是“更相减损”法。所以更相减损法>也叫等值算法。
代码:
#include测试及测试代码与平均运行时间:
测试代码:
#includeStein算法由J. Stein 1961年提出,这个方法也是计算两个数的最大公约数。来研究一下最大公约数的性质,发现有 gcd( kx,ky ) = kgcd( x,y ) 这么一个非常好的性质。
试取 k=2,则有 gcd( 2x,2y ) = 2 * gcd( x,y )。很快联想到将两个偶数化小的方法。
那么一奇一个偶以及两个奇数的情况如何化小呢?
先来看看一奇一偶的情况: 设有2x和y两个数,其中y为奇数。因为y的所有约数都是奇数,所以 a = gcd( 2x,y ) 是奇数。
根据2x是个偶数不难联想到,a应该是x的约数。
我们来证明一下:
(2x)%a=0,设2x=na,因为a是奇数,2x是偶数,则必有n是偶数。
又因为 x=(n/2)*a,所以 x%a=0,即a是x的约数。
因为a也是y的约数,所以a是x和y的公约数,有 gcd( 2x,y ) <= gcd( x,y )。
因为gcd( x,y )明显是2x和y的公约数,又有gcd( x,y ) <= gcd( 2x,y ),
所以 gcd( 2x,y ) = gcd( x,y )。
至此,我们得出了一奇一偶时化小的方法。
再来看看两个奇数的情况:
设有两个奇数x和y,不妨设x>y,注意到x+y和x-y是两个偶数,
则有gcd( x+y,x-y ) = 2 * gcd( (x+y)/2,(x-y)/2 ),
那么 gcd( x,y ) 与 gcd( x+y,x-y ) 以及 gcd( (x+y)/2,(x-y)/2 ) 之间是不是有某种联系呢?
为了方便设 m=(x+y)/2 ,n=(x-y)/2 ,容易发现 m+n=x ,m-n=y 。
设 a = gcd( m,n ),则 m%a=0,n%a=0 ,
所以 (m+n)%a=0,(m-n)%a=0 ,即 x%a=0 ,y%a=0 ,
所以a是x和y的公约数,有 gcd( m,n )<= gcd(x,y)。
再设 b = gcd( x,y )肯定为奇数,则 x%b=0,y%b=0 ,
所以 (x+y)%b=0 ,(x-y)%b=0 ,
又因为x+y和x-y都是偶数,跟前面一奇一偶时证明a是x的约数的方法相同,
有 ((x+y)/2)%b=0,((x-y)/2)%b=0 ,即 m%b=0 ,n%b=0 ,
所以b是m和n的公约数,有 gcd( x,y ) <= gcd( m,n )。
所以 gcd( x,y ) = gcd( m,n ) = gcd( (x+y)/2,(x-y)/2 )。
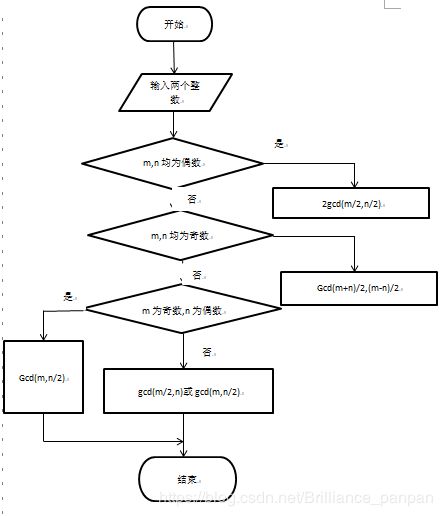
*整理一下,对两个正整数 x>y :
1.均为偶数 gcd( x,y ) =2gcd( x/2,y/2 );
2.均为奇数 gcd( x,y ) = gcd( (x+y)/2,(x-y)/2 );
2.x奇y偶 gcd( x,y ) = gcd( x,y/2 );
3.x偶y奇 gcd( x,y ) = gcd( x/2,y ) 或 gcd( x,y )=gcd( y,x/2 );
现在已经有了递归式,还需要再找出一个退化情况。注意到 gcd( x,x ) = x ,就用这个。
①函数非递归调用
#include测试及测试代码与平均运行时间:
测试代码:
#include②函数递归调用
#include测试及测试代码与平均运行时间:
测试代码:
#include