机器学习方法：回归（一）：线性回归Linear regression

转载请注明：本文出自Bin的专栏blog.csdn.net/xbinworld。

开一个机器学习方法科普系列：做基础回顾之用，学而时习之；也拿出来与大家分享。数学水平有限，只求易懂，学习与工作够用。周期会比较长，因为我还想写一些其他的，呵呵。

content: 
linear regression, Ridge, Lasso 
Logistic Regression, Softmax 
Kmeans, GMM, EM, Spectral Clustering 
Dimensionality Reduction: PCA、LDA、Laplacian Eigenmap、 LLE、 Isomap（修改前面的blog） 
SVM 
ID3、C4.5 
Apriori，FP 
PageRank 
minHash, LSH 
Manifold Ranking，EMR 
待补充 
… 
…

开始几篇将详细介绍一下线性回归linear regression，以及加上L1和L2的正则的变化。后面的文章将介绍逻辑回归logistic regression，以及Softmax regression。为什么要先讲这几个方法呢？因为它们是机器学习/深度学习的基石（building block）之一，而且在大量教学视频和教材中反复被提到，所以我也记录一下自己的理解，方便以后翻阅。这三个方法都是有监督的学习方法，线性回归是回归算法，而逻辑回归和softmax本质上是分类算法（从离散的分类目标导出），不过有一些场合下也有混着用的——如果目标输出值的取值范围和logistic的输出取值范围一致。

ok，废话不多说。

1、Linear Regression

可以说基本上是机器学习中最简单的模型了，但是实际上其地位很重要（计算简单、效果不错，在很多其他算法中也可以看到用LR作为一部分）。

先来看一个小例子，给一个“线性回归是什么”的概念。图来自[2]。

 
假设有一个房屋销售的数据如下： 
面积(m^2) 销售价钱（万元） 
123 250 
150 320 
87 160 
102 220 
… …

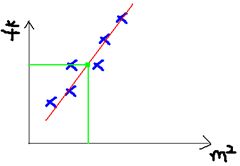
当我们有很多组这样的数据，这些就是训练数据，我们希望学习一个模型，当新来一个面积数据时，可以自动预测出销售价格（也就是上右图中的绿线）；这样的模型必然有很多，其中最简单最朴素的方法就是线性回归，也就是我们希望学习到一个线性模型（上右图中的红线）。不过说是线性回归，学出来的不一定是一条直线，只有在变量x是一维的时候才是直线，高维的时候是超平面。

定义一下一些符号表达，我们通常习惯用 X=(x1,x2,...,xn)T∈Rn×p 表示数据矩阵，其中 xi∈Rp 表示一个p维度长的数据样本； y=(y1,y2,...,yn)T∈Rn 表示数据的label，这里只考虑每个样本一类的情况。

线性回归的模型是这样的，对于一个样本 xi ，它的输出值是其特征的线性组合： 

f(xi)=∑m=1pwmxim+w0=wTxi

其中， w0 称为截距，或者bias，上式中通过增加 xi0=1 把 w0 也吸收到向量表达中了，简化了形式，因此实际上 xi 有 p+1 维度。

线性回归的目标是用预测结果尽可能地拟合目标label，用最常见的Least square作为loss function： 

J(w)=1n∑i=1n(yi−f(xi))2=1n∥y−Xw∥2

从下图来直观理解一下线性回归优化的目标——图中线段距离（平方）的平均值，也就是最小化到分割面的距离和。 

也就是很多中文教材中提到的最小二乘；线性回归是convex的目标函数，并且有解析解： 

w^=(XTX)−1XTy

线性回归到这里就训练完成了，对每一个样本点的预测值是 f(xi)=yi^=w^Txi 。所以： 

y^=Xw^=X(XTX)−1XTy

接下来看一下我们寻找到的预测值的一个几何解释：从上面的解析解 w^=(XTX)−1XTy 可以得到 XT(y^−y)=0 （垂直的向量相乘=0），因此实际上 y^ 是 y 在平面 X （由列向量 x1 和 x2 张成，假设只有两维）上的投影。 

ok，一般介绍线性回归的文章到这里也就结束了，因为实际使用中基本就是用到上面的结果，解析解计算简单而且是最优解；当然如果求逆不好求的话就可以不用解析解，而是通过梯度下降等优化方法来求最优解，梯度下降的内容不在本篇中，后面讲逻辑回归会说到。也可以看我前面写的今天开始学PRML第5章中有写到，或者直接翻阅wikipedia:gradient descent。

不过在这里我再稍微提几个相关的分析，可以参考ESL[3]的第3章中的内容。前面我们对数据本身的分布是没有任何假设的，本节下面一小段我们假设观察值 yi 都是不相关的，并且方差都是 σ2 ，并且样本点是已知（且是中心化过了的，均值为0）的。于是我们可以推出协方差矩阵 

Var(β^)=(XTX)−1σ2

证明： 

Var(β^)=(XTX)−1XTyytX(XTX)−1=(XTX)−1σ2

要估计方差 σ2 ，可以用 

σ^2=1n−p−1∑i=1n(yi−y^i)2

这里和一般的方差的形式看起来不同，分母是 n−p−1 而不是 n ，是因为这样的估计才是 σ2 的无偏估计。 
证明：

E(σ^2)=E(1n−p−1∑i=1n(yi−y^i)2)=E(1n−p−1[y−X(XTX)−1XTy]T[y−X(XTX)−1XTy]）=E(1n−p−1yT[In−X(XTX)−1XT]y）=nσ2n−p−1−1n−p−1tr(X(XTX)−1XTyyT)=nσ2n−p−1−σ2n−p−1tr(X(XTX)−1XT)=nσ2n−p−1−(p+1)σ2n−p−1=σ2

好，第一篇就写到这里。这个系列是从0开始的基础复习记录，力求清晰易懂。下一篇lasso和ridge regression。

参考资料 
[1]http://freemind.pluskid.org/machine-learning/sparsity-and-some-basics-of-l1-regularization/ 
[2]http://www.cnblogs.com/LeftNotEasy/archive/2010/12/05/mathmatic_in_machine_learning_1_regression_and_gradient_descent.html 
[3]The Elements of Statistical Learning，ch3

顶