【Leetcode】从 2sum 到 3sum, 4sum, Ksum
在上一篇博客【Leetcode】2sum 中,已经介绍了2sum的问题以及相应解法,现在来看看由这个问题延伸出来的3sum,4sum以及Ksum。
首先来看3sum,这个问题在Leetcode中也有一个问题形式(Leetcode 15),如下:
Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.
Note:
The solution set must not contain duplicate triplets.
Example:
Given array nums = [-1, 0, 1, 2, -1, -4],
A solution set is:
[
[-1, 0, 1],
[-1, -1, 2]
]
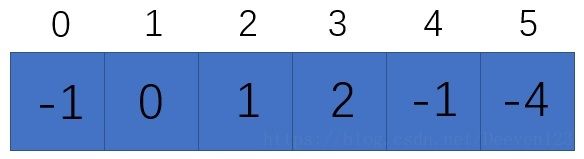
之前在做 2sum 时,用了首尾指针的方法,这里解决3sum同样适用。先给一个图如下,表示原始给定的数组,方便理解:
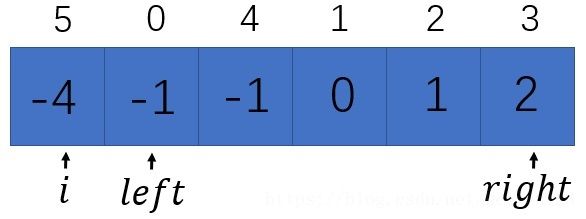
图中上面数字是数组的元素序号,蓝色框中是元素的值。对数组进行稳定性排序(从小到大)后,得到下面的图:
由于需要计算 a + b + c = 0 a+b+c=0 a+b+c=0,可以固定 a a a,那么就可以转化为 b + c = − a b+c=-a b+c=−a 的 2sum 问题了。那么 a a a 应该怎么固定呢?答案是从最小的元素开始循环遍历,当遍历取定一个值时就相当于在这个时刻固定了 a a a,上面图中指针 i i i 对应的元素就是 a a a,而 2sum 之前在上一篇博客【Leetcode】2sum 中是用的首尾相夹的方法做的,也就是说 b b b 和 c c c 分别对应上述 left 指针和 right 指针的元素。
需要注意的几点是:
(1) left 指针和 right 指针在指针 i i i 的右侧;
(2) 当 i i i 固定时,在 i i i 的右边利用“首尾相夹”的方法找出满足条件的 left 和 right;
(3) 当 i i i 对应的元素为正数时,循环可以终止了,不用再进行下去。因为三个正数的和不可能为0。
Python代码如下:
def threeSum(nums, target):
lists = []
for i in range(len(nums)):
lists.append([nums[i], i])
lists = sorted(lists, key = lambda s:s[0])
results = [] # 用于存储满足条件的结果
for i in range(len(nums)-2):
if i>0 and lists[i][0]==lists[i-1][0]:
continue
if lists[i][0]>0: #三个正数和不可能等于0(当target=0或负数时才有此条件)
break
l = i+1; r = len(nums)-1
while(l<r):
if lists[i][0]+lists[l][0]+lists[r][0]<target:
l+=1
elif lists[i][0]+lists[l][0]+lists[r][0]>target:
r-=1
else:
results.append([lists[i][0], lists[l][0], lists[r][0]])
# 由于一个 i对应的解可能不只一个,所以当上面找到结果不能break,要继续夹
l+=1
r-=1
return results
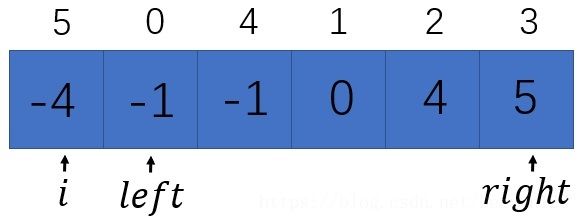
上面的代码中 target=0。需要注意的是,虽然上面的思路可以找到所有满足条件的结果,但是在速度上可以进一步优化。下面用一个图来详细说明一下(为了方便解释说明,将之前数组的最后两个元素改成了4和5,此处仅仅是为了方便说明优化的情况,并不影响解题思路):
在上面这个图中,当 i i i 固定为 -4 时,它的右边是2sum的解法。当 left 指针指向 -1,right 指针指向 5 时,得到满足条件的解 [-4, -1, 5]。由于题目要求不能有重复解出现,所以下一组解在 a a a 仍然是 -4 的情况下, b b b 不可能是 -1, c c c 也不可能是 5。按照之前的代码,当 a a a 固定为 -4 得到一组解之后,left 指针会变成 left+1,right 指针会变成 right-1,但是这样会显得有点慢。比如上面的这个例子,在 left 指向 -1 得到满足条件的结果后,它的右边还是 -1,所以没有必要用 left = left +1,而应该直接跳到右边与它不相等的数值上去。
改进后的Python代码如下:
def threeSum(nums, target):
lists = []
for i in range(len(nums)):
lists.append([nums[i], i])
lists = sorted(lists, key = lambda s:s[0])
results = [] # 用于存储满足条件的结果
for i in range(len(nums)-2):
if i>0 and lists[i][0]==lists[i-1][0]:
continue
if lists[i][0]>0: #三个正数和不可能等于0(当target=0或负数时才有此条件)
break
l = i+1; r = len(nums)-1
while(l<r):
if lists[i][0]+lists[l][0]+lists[r][0]<target:
l+=1
elif lists[i][0]+lists[l][0]+lists[r][0]>target:
r-=1
else:
while(l<r and lists[l+1][0] == lists[l][0]):
l+=1
while(l<r and lists[r-1][0] == lists[r][0]):
r-=1
results.append([lists[i][0], lists[l][0], lists[r][0]])
# 由于一个 i对应的解可能不只一个,所以当上面找到结果不能break,要继续夹
l+=1
r-=1
return results
上述代码注意三点:
(1) 直接用的 target 作为输入,表明不局限于题目中的 a + b + c = 0 a+b+c=0 a+b+c=0,可以适用于 a + b + c = a+b+c= a+b+c=target 的任意情况,但是注意如果将 target 换成正数,上述代码中的判断语句条件"if lists[i][0]>0" 可以去掉;
(2) 用 lists 来存储排序后的 nums, 而没有用 nums.sort() 来直接在 nums 上排序是因为保留了排序前的序号关系,存储在了 lists[ i i i][1] 里面,可以适用于变形后的 3sum 题型,比如说让你输出相应结果和对应序号;
(3) 题目要求不能有重复的结果,而“首尾相夹”的方法得到的结果可能有重复的,比如 [0, 0, 0, 0, 0, 0, 0]满足条件的解肯定是 [0, 0, 0],但是随着指针的移动会不会结果变成 [[0, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 0]]呢? 答案是不会。虽然没有加上类似于“if result in results”这样的判断语句,但是代码中的最后两个while循环已经解决了重复的问题。因为数组是单调递增的(严格说是单调不减),所以满足相同的解必须相邻。比如说 [-4, -1, -1, 3, 5, 5],那么解为 [-4, -1, 5]。设 [ a 1 a_1 a1, b 1 b_1 b1, c 1 c_1 c1] 、 [ a 2 a_2 a2, b 2 b_2 b2, c 2 c_2 c2] 为两个相同解,那么必有 a 1 a_1 a1与 a 2 a_2 a2 相邻、 b 1 b_1 b1与 b 2 b_2 b2 相邻、 c 1 c_1 c1与 c 2 c_2 c2 相邻,而这些已经在上述代码中用 "if i>0 and lists[i][0]==lists[i-1][0]"以及后面两个 while 循环给过滤掉了,所以不可能有重复的了。如果不加这些过滤条件,直接用每次得到的满足题意的 result 来判断是否 “if result in results”,也可以得到正确的结果,虽然都是O( n 2 n^2 n2)的复杂度,但后者在Leetcode的样例测试中容易超时(LTE)。
讨论完了 3sum 的题之后,在Leetcode上面还有个 3sum closet 的题,这个就是 3sum 的一般情形。下面先给出Leetcode上的问题(Leetcode 16):
Given an array nums of n integers and an integer target, find three integers in nums such that the sum is closest to target. Return the sum of the three integers. You may assume that each input would have exactly one solution.
Example:
Given array nums = [-1, 2, 1, -4], and target = 1.
The sum that is closest to the target is 2. (-1 + 2 + 1 = 2).
这个就是将之前 3sum 中 target=0 换成了 terget=1,而且将 a + b + c = a+b+c= a+b+c= target 换成了 a + b + c → a+b+c\rightarrow a+b+c→ target,这里的 “ → \rightarrow →” 表示“最接近于”。那么,问题的难点在于怎么去衡量这个“最接近于”。这个难点如果清楚了,那么问题就解决了。
这个题的思路其实也不算太难。先将其简化成 “求一个数组中任意两个数的 sum 最接近于 target 的那个 sum 值”,即将 “三个数的和” 降为 “两个数的和”,如果这个 “两个数的和” 的问题解决了,那么 “三个数的和” 的问题也会解决。
给出下面这个数组:
当 i i i 固定为 -4 时,left 指针和 right 指针初始化情况下分别取的是 i + 1 i+1 i+1 和最后一个元素位置,其和为 a + b + c = 1 a+b+c=1 a+b+c=1,比如现在的 target=0,那么当 a + b + c a+b+c a+b+c 的和不等于 target 的情况下,会继续寻找,直到遍历所有位置的和,找出其中距离 target 最小的,如果在遍历的中途有 a + b + c = a+b+c= a+b+c= target,那么循环就可以在中途终止。
现在的问题是,此刻的 a + b + c = 1 a+b+c=1 a+b+c=1,它并不等于target=0,不能判断它是否离 target 最近,需要继续寻找,那么下一步应该让 left = left+1,还是 right = right-1,还是两者都执行呢?解决这个问题的关键点在于:如果 left 右移,那么 a + b + c a+b+c a+b+c 会增大;如果 right 左移,那么 a + b + c a+b+c a+b+c 会减小。所以只需判断 “left 右移得到的和”,与 “right 左移得到的和”,两者哪个距离 target 近就可以了。
Python 代码如下:
def threeSumII(nums, target):
lists = []
for i in range(len(nums)):
lists.append([nums[i], i])
lists = sorted(lists, key = lambda s:s[0])
results = sum(nums[:3]) # 初始化结果
for i in range(len(nums)-2):
if i>0 and lists[i][0]==lists[i-1][0]:
continue
l = i+1; r = len(nums)-1
while(l<r):
tmp_sum = lists[i][0]+lists[l][0]+lists[r][0]
if abs(tmp_sum-target)>abs(results-target) and tmp_sum<results:
l+=1
elif abs(tmp_sum-target)>abs(results-target) and tmp_sum>results:
r-=1
else:
results = tmp_sum
if r-l>=1:
tmp_sum1 = lists[i][0]+lists[l+1][0]+lists[r][0]
tmp_sum2 = lists[i][0]+lists[l][0]+lists[r-1][0]
if abs(tmp_sum1-target)<abs(tmp_sum2-target):
l+=1
else:
r-=1
return results
需要注意的是:
注:这里去掉了之前在 3sum 中(见上面的第二部代码)的最后两个 while 语句,因为此处不需要判重,如果增加了这两个 while 语句,反而会出错。比如数组 [-20, -19, -19, -18, -6], target=-59,其最优答案应该是:-20+(-19)+(-19)=-58,如果增加了判断重复的两个 while 语句,那么 left 指针会跳过相同的 -19变为指向 -18,而 right 指针又比 left 指针大,所以 right 指针将指不到 -19上去。
下面再来看 Leetcode 上的 4sum 问题(Leetcode 18),如下:
Given an array nums of n integers and an integer target, are there elements a, b, c, and d in nums such that a + b + c + d = target? Find all unique quadruplets in the array which gives the sum of target.
Note:
The solution set must not contain duplicate quadruplets.
Example:
Given array nums = [1, 0, -1, 0, -2, 2], and target = 0.
A solution set is:
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]
这个题目是可以看作之前 3sum 的进一步升级,但是其主要思路还是没变,即“首尾指针法”。这题需要求解的是 a + b + c + d = a+b+c+d= a+b+c+d= target,对于每一次循环遍历,相当于固定 a a a,那么就变成了求解 b + c + d = b+c+d= b+c+d= target − a -a −a 的 3sum 问题了,比较容易。
Python 代码如下:
def fourSum(nums, target):
lists = []
for i in range(len(nums)):
lists.append([nums[i], i])
lists = sorted(lists, key = lambda s:s[0])
results = [] # 用于存储满足条件的结果
for i in range(len(nums)-3):
if i>0 and lists[i][0]==lists[i-1][0]:
continue
for j in range(i+1, len(nums)-2):
if j>i+1 and lists[j][0]==lists[j-1][0]:
continue
l = j+1; r = len(nums)-1
while(l<r):
if lists[i][0]+lists[j][0]+lists[l][0]+lists[r][0]<target:
l+=1
elif lists[i][0]+lists[j][0]+lists[l][0]+lists[r][0]>target:
r-=1
else:
while(l<r and lists[l+1][0] == lists[l][0]):
l+=1
while(l<r and lists[r-1][0] == lists[r][0]):
r-=1
results.append([lists[i][0], lists[j][0], lists[l][0], lists[r][0]])
# 由于一个 i对应的解可能不只一个,所以当上面找到结果不能break,要继续夹
l+=1
r-=1
return results
上述代码可以简化为如下:
def fourSum(nums, target):
nums.sort()
results = []
for i in range(len(nums)-3):
for j in range(i + 1, len(nums)-2):
l = j + 1
r = len(nums) -1
while(l<r):
if nums[i] + nums[j] + nums[l] + nums[r] < target:
l+=1
elif nums[i] + nums[j] + nums[l] + nums[r] > target:
r-=1
else:
result = [nums[i],nums[j],nums[l],nums[r]]
if result not in results:
results.append(result)
l+=1
r-=1
return results
但是将 4sum 转化为 3sum 问题去求解之后,有一个缺陷,就是时间复杂度太高,为 O( n 3 n^3 n3)。其实,还有一个时间复杂度为 O( n 2 n^2 n2) 的做法,即把 a + b + c + d = a+b+c+d= a+b+c+d= target 变成 a + b = a+b= a+b= target − ( c + d ) -(c+d) −(c+d) 的形式,那么就可以转化为 2sum 的做法,而 2sum 的时间复杂度为 O( n n n) 。
Python 代码如下:
def fourSum(nums, target):
nums.sort()
results, dicts = set(), {}
# 之所以将results设置为集合而不是列表,是因为后面的结果有重复,用列表还要进一步去重
# 先将所有“二元组的和”放入字典,键为“和”,值为对应二元,相同和的二元追加到后面
# 例如 5=1+4=2+3, 那么字典就是:{5:[(1,4),(2,3)]}
for i in range(len(nums)):
for j in range(i+1, len(nums)):
sums1 = nums[i] + nums[j]
if sums1 not in dicts.keys():
dicts[sums1] = [(i,j)]
else:
dicts[sums1].append((i,j))
for i in range(len(nums)):
for j in range(i+1, len(nums)-2):
sums2 = target - nums[i] -nums[j]
if sums2 in dicts.keys():
for term in dicts[sums2]:
if term[0] > j:
results.add((nums[i], nums[j], nums[term[0]], nums[term[1]]))
return list(map(list, results))
关于 4sum 问题,Leetcode 上面还有它的另一个类似问题,叫做 4sum II 问题(Leetcode 454),题目如下:
Given four lists A, B, C, D of integer values, compute how many tuples (i, j, k, l) there are such that A[i] + B[j] + C[k] + D[l] is zero.
To make problem a bit easier, all A, B, C, D have same length of N where 0 ≤ N ≤ 500. All integers are in the range of -228 to 228 - 1 and the result is guaranteed to be at most 231 - 1.
Example:
Input:
A = [ 1, 2]
B = [-2,-1]
C = [-1, 2]
D = [ 0, 2]
Output:
2
Explanation:
The two tuples are:
1.(0, 0, 0, 1) -> A[0] + B[0] + C[0] + D[1] = 1 + (-2) + (-1) + 2 = 0
2.(1, 1, 0, 0) -> A[1] + B[1] + C[0] + D[0] = 2 + (-1) + (-1) + 0 = 0
这个问题相比于 4sum 问题,只是把一个数组变成了四个,其思路是不变的。还是可以将其转化为 3sum 或者 2sum 的问题来做。下面给出时间复杂度为 O( n 2 n^2 n2) 的代码,做法与之前的 4sum 基本一样。
Python 代码如下:
def fourSumII(A, B, C, D):
count = 0
length = len(A)
dicts = {}
for i in range(length):
for j in range(length):
sums1 = A[i]+B[j]
if sums1 not in dicts:
dicts[sums1] = 1
else:
dicts[sums1] += +1
for i in range(length):
for j in range(length):
sums2 = -(C[i]+D[j])
if sums2 in dicts.keys():
count += dicts[sums2]
return count
关于 2sum、3sum、4sum 基本的解题思路要么是“首尾指针法”,要么是转化为 2sum 的哈希法。哈希法的好处是快,但是需要构造字典,消耗了内存空间,相当于用空间换取时间。对于 Ksum 的问题,最基本的解法就是层层剥离,将 Ksum 转化为 (K-1)sum,依次下去,此时的时间复杂度为 O( n k − 1 n^{k-1} nk−1),通过“首尾指针法”来寻找结果。当然,也可以尝试将 Ksum 转化为 2sum 或 4sum等,利用 hash 的方法来做。