周志华机器学习 CH3.5 编程实现线性判别分析
方法一:利用sklearn库函数实现
import numpy as np
import matplotlib.pyplot as plt
'''
# LDA via sklearn
'''
from sklearn import model_selection
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn import metrics
fr = open("3.0.txt")
dataSet = np.loadtxt(fr, delimiter = ",")
X = dataSet[:, 1:3]
Y = dataSet[:, 3]
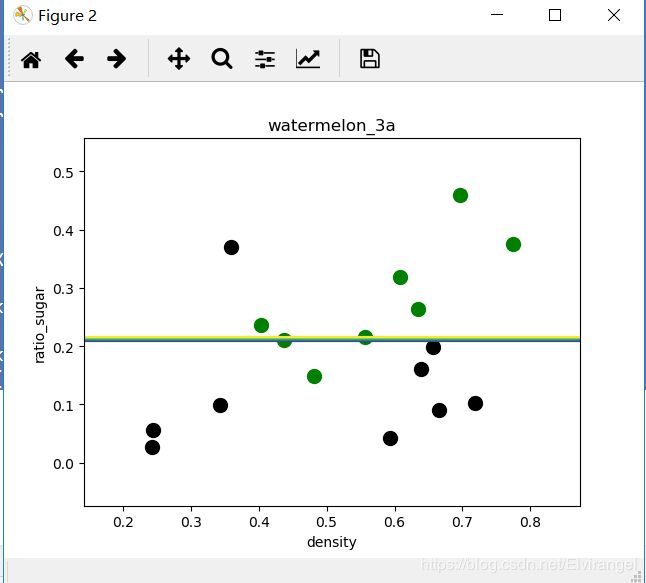
# draw scatter diagram to show the raw data
f1 = plt.figure(1)
plt.title('watermelon_3a')
plt.xlabel('density')
plt.ylabel('ratio_sugar')
plt.scatter(X[Y == 0,0], X[Y == 0,1], marker = 'o', color = 'k', s=100, label = 'bad')
plt.scatter(X[Y == 1,0], X[Y == 1,1], marker = 'o', color = 'g', s=100, label = 'good')
plt.legend(loc = 'upper right')
X_train,X_test,Y_train,Y_test=model_selection.train_test_split(X,Y,test_size=0.5,random_state = 0)
#进行拟合
lda_model=LinearDiscriminantAnalysis(solver = 'lsqr',shrinkage = None).fit(X,Y)
y_pred=lda_model.predict(X_test)
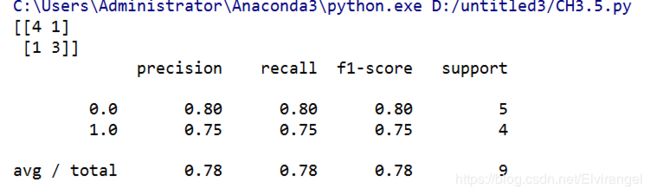
print(metrics.confusion_matrix(Y_test,y_pred))
print(metrics.classification_report(Y_test,y_pred))
#画出决策边界
f2=plt.figure(2)
h=0.01
X0_min,X0_max=X[:,0].min()-0.1,X[:,0].max()+0.1
X1_min,X1_max=X[:,1].min()-0.1,X[:,1].max()+0.1
X0,X1=np.meshgrid(np.arange(X0_min,X0_max,h),np.meshgrid(np.arange(X1_min,X1_max,h)))
z=lda_model.predict(np.c_[X0.ravel(),X1.ravel()])
print(z.shape)
# Put the result into a color plot
print(X0.shape)
z=z.reshape(X0.shape)
print(z)
print(z.shape)
plt.contour(X0,X1,z)
# Plot also the training pointsplt.title('watermelon_3a')
plt.title('watermelon_3a')
plt.xlabel('density')
plt.ylabel('ratio_sugar')
plt.scatter(X[Y == 0,0], X[Y == 0,1], marker = 'o', color = 'k', s=100, label = 'bad')
plt.scatter(X[Y == 1,0], X[Y == 1,1], marker = 'o', color = 'g', s=100, label = 'good')
plt.show()
运行结果:
方法二:利用python自己编程实现
import numpy as np
import matplotlib.pyplot as plt
def loadDataSet(fileName):
'''
fr=open(fileName)
X=[];Y=[]
for line in fr.readlines():
lineArr=line.strip().split(',')
X.append([float(lineArr[1]),float(lineArr[2])])
Y.append(lineArr[3])
'''
fr=open(fileName)
dataSet=np.loadtxt(fr,delimiter=",")
X=dataSet[:,1:3]
Y=dataSet[:,3]
print(type(X),type(Y))
return np.array(X),np.array(Y)
def plotDataSet(X,Y):
# 绘制数据集
f1 = plt.figure()
plt.title("watermelon_3a")
plt.xlabel("密度")
plt.ylabel("含糖量")
plt.scatter(X[Y == 0, 0], X[Y == 0, 1], marker = 'o', color = 'k', s = 100, label = 'bad')
plt.scatter(X[Y == 1, 0], X[Y == 1, 1], marker = 'o', color = 'g', s = 100, label = 'good')
plt.legend(loc = 'upper right')
plt.show()
# 求类内散度矩阵
def Sw(X,Y):
u=[]
u.append(np.mean(X[Y==0],axis=0)) #column means
u.append(np.mean(X[Y==1],axis=0))
u=np.array(u)
m,n=np.shape(X)
sw=np.zeros((n,n))
X0=X[Y==0]
X1=X[Y==1]
# !!!!!
# 一定注意要把u变成矩阵!!!!
# 因为u.shape=(1,2),直接u.T转置还是一个一维的数组,参与运算出错!!
# 因为u=[1,2],u.T=[1,2]
# 变成矩阵u=[[1,2]],u.T=[[1],[2]]
# 弄了一天!!才发现这里出了问题!!!!
#(或者:u=u.reshape((2,1)),这样之后在转置,和np.mat(u)效果一样!)
for i in range(np.shape(X0)[0]):
sw+=np.dot(np.mat((X0[i]-u[0])).T,np.mat(X0[i]-u[0]))
for i in range(np.shape(X1)[0]):
sw+=np.dot(np.mat((X1[i]-u[1])).T,np.mat(X1[i]-u[1]))
'''
for i in range(m):
if Y[i]==0:
x_temp=X[i]-u[0]
print("temp= ",np.array(x_temp).T,"temp.T= ",(x_temp))
else:
x_temp=X[i]-u[1]
# print(x_temp.T)
sw+=np.dot(np.mat(x_temp).T,np.mat(x_temp))
print(i, " ", sw)
'''
print(sw)
return sw,u
#计算w
def wFunction(sw,u):
m,n=np.shape(X)
sw_inv=np.linalg.pinv(sw)
w=np.dot(sw_inv,(u[0]-u[1]).T)
return w
# draw projective point on the line
# 计算投影点的坐标,
# 利用直线和垂直线的斜率相乘=1,求两直线交点坐标
def GetProjectivePoint_2D(point, line):
a = point[0]
b = point[1]
k = line[0]
t = line[1]
if k == 0: return [a, t] # 平行于横轴
elif k == np.inf: return [0, b] # 平行于纵轴
x = (a+k*b-k*t) / (k*k+1) #斜线
y = k*x + t
return [x, y]
if __name__=="__main__":
X,Y=loadDataSet("3.0.txt")
#print(X)
#print(Y)
#plotDataSet(X,Y)
sw,u=Sw(X,Y)
w=wFunction(sw,u)
print(w)
f2 = plt.figure(2)
p0_x0 = -X[:, 0].max()
p0_x1 = (-w[0]/w[1])*p0_x0
p1_x0 = X[:, 0].max()
p1_x1 = (-w[0]/w[1])*p1_x0
plt.title('watermelon_3a - LDA')
plt.xlabel('density')
plt.ylabel('ratio_sugar')
plt.scatter(X[Y == 0, 0], X[Y == 0, 1], marker = 'o', color = 'k', s = 10, label = 'bad')
plt.scatter(X[Y == 1, 0], X[Y == 1, 1], marker = 'o', color = 'g', s = 10, label = 'good')
plt.legend(loc = 'upper right')
plt.plot([p0_x0, p1_x0], [p0_x1, p1_x1])
m, n = np.shape(X)
for i in range(m):
x_p = GetProjectivePoint_2D([X[i][0], X[i][1]], [-w[0]/w[1], 0])
if Y[i] == 0:
plt.plot(x_p[0], x_p[1], 'ko', markersize = 5)
if Y[i] == 1:
plt.plot(x_p[0], x_p[1], 'go', markersize = 5)
plt.plot([x_p[0], X[i, 0]], [x_p[1], X[i, 1]], 'c--', linewidth = 0.3)
plt.show()运行结果:
删除一个离群的训练样本后,得以改善: