树的递归与非递归遍历算法

树的递归与非递归遍历算法

树的遍历

遍历定义——指按某条搜索路线遍访每个结点且不重复（又称周游）
遍历用途——它是树结构插入、删除、修改、查找和排序运算的前提，是二叉树一切运算的基础和核心
遍历方法——牢记一种约定，对每个结点的查看都是“先左后右”

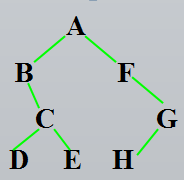
实例：

先序遍历：ABCDEFGH

中序遍历：BDCEAFHG

后序遍历：DECBHGFA

树遍历的口诀

DLR—先序遍历，即先根再左再右
LDR—中序遍历，即先左再根再右
LRD—后序遍历，即先左再右再根

树的递归遍历代码

树的先序遍历

代码块语法遵循标准C/C++代码

/*
* 问题描述：树的先序递归描述
* C/C++ 语言
*
* @author Erice_s
* binbin_Erices@163.com
* @date 2017/10/28
*
*/
typedef struct BiTNode
{
    int data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

void preOrder(BiTNode *root)
{
    if (root==NULL)
        return;
    printf("%d ",root->data);

    preOrder(root->lchild);

    preOrder(root->rchild);
}

---

树的中序遍历

代码块语法遵循标准C/C++代码

/*
* 问题描述：树的中序递归描述
* C/C++ 语言
*
* @author Erice_s
* binbin_Erices@163.com
* @date 2017/10/28
*
*/
typedef struct BiTNode
{
    int data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

void inOrder(BiTNode *root)
{
    if (root)
    {
        inOrder(root->lchild);
        printf("%d ", root->data);
        inOrder(root->rchild);
    }
}

---

树的后序遍历

代码块语法遵循标准C/C++代码

/*
* 问题描述：树的后序递归描述
* C/C++ 语言
*
* @author Erice_s
* binbin_Erices@163.com
* @date 2017/10/28
*
*/
typedef struct BiTNode
{
    int data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

void postOrder(BiTNode *root)
{
    if (root)
    {
        postOrder(root->lchild);
        postOrder(root->rchild);
        printf("%d ", root->data);  
    }
}

递归遍历思想

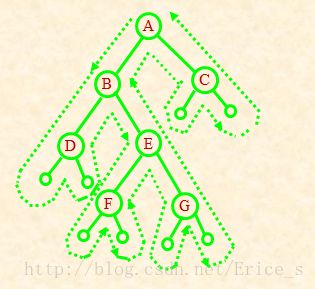
从前面的三种遍历算法可以知道：如果将printf语句抹去，从递归的角度看，这三种算法是完全相同的，或者说这三种遍历算法的访问路径是相同的，只是访问结点的时机不同

从虚线的出发点到终点的路径上，每个结点经过3次
第1次经过时访问＝先序遍历
第2次经过时访问＝中序遍历
第3次经过时访问＝后序遍历

二叉树遍历的时间效率和空间效率
时间效率:O(n) //每个结点只访问一次
空间效率:O(n) //栈占用的最大辅助空间（精确值：树深为k的递归遍历需要k+1个辅助单元！）

树的非递归遍历

树的先序非递归遍历

算法思想：若p所指的结点不为空，则访问该节点，然后将该节点的地址入栈，然后再将p指向其左孩子结点；若p所指的结点为空，则从堆栈中退出栈顶元素，将p指向其右孩子结点。重复步骤，知道p==NULL&&堆栈为空，遍历结束。

/*
* 问题描述：树的先序非递归遍历
* C/C++ 语言
*
* @author Erice_s
* [email protected]
* @date 2017/10/28
*
*/
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 
#define   MAX_STACK  50

using namespace std;

typedef struct BiTNode
{
    int data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

//创建二叉树  从键盘接受数据 先序遍历递归算法
BiTree CreateBT()
{
    char ch;
    BiTree T;

    scanf("%c", &ch);
    if (ch == '#')
        return NULL;
    else
    {
        T = (BiTree)malloc(sizeof(BiTNode));
        T->data = ch;
        T->lchild = CreateBT();
        T->rchild = CreateBT();
    }

    return T;
}
//树的先序非递归遍历算法
void preOrder(BiTree T)
{
    BiTree STACK[MAX_STACK], p = T;
    int top = -1;
    while (p != NULL || top != -1)
    {
        while (p != NULL)
        {
            printf("%c ", p->data);
            STACK[++top] = p;
            p = p->lchild;
        }
        p = STACK[top--];
        p = p->rchild;
    }
}

int main(void)
{
    BiTree root;
    cout << "请初始化树：";
    root = CreateBT();

    cout << "树的先序非递归遍历：";
    preOrder(root);
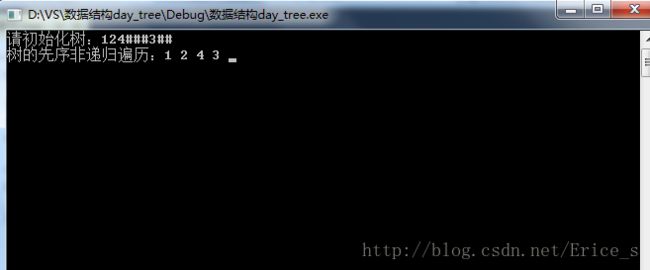
    return 0;
}

先序遍历运行结果

树的中序非递归遍历

算法思想：
步骤1：
如果结点有左子树，该结点入栈；
如果结点没有左子树，访问该结点；
步骤2：
如果结点有右子树，重复步骤1；
如果结点没有右子树（结点访问完毕），根据栈顶指示回退，访问栈顶元素，并访问右子树，重复步骤1
如果栈为空，表示遍历结束。
注意：入栈的结点表示，本身没有被访问过，同时右子树也没有被访问过。

/*
* 问题描述：树的中序非递归描述
* C/C++ 语言
*
* @author Erice_s
* [email protected]
* @date 2017/10/28
*
*/
#define _CRT_SECURE_NO_WARNINGS
#include 
#include 

using namespace std;

typedef struct BiTNode
{
    int data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

//创建二叉树  从键盘接受数据 先序遍历递归算法
BiTree CreateBT()
{
    char ch;
    BiTree T;

    scanf("%c",&ch);
    if (ch == '#')
        return NULL;
    else
    {
        T = new BiTree;
        T->data = ch;
        T->lchild = CreateBT();
        T->rchild = CreateBT();
    }

    return T;
}

//销毁一棵树
void  BiTree_Free(BiTNode* T)
{
    if (T != NULL)
    {
        if (T->rchild != NULL) BiTree_Free(T->rchild);
        if (T->lchild != NULL) BiTree_Free(T->lchild);
        if (T != NULL)
        {
            delete T;
            T = NULL;
        }
    }
}


//一直往左走找到中序遍历的起点
BiTNode *goL(BiTNode *T, stack&s)
{
    if (T == NULL)
        return NULL;
    while (T->lchild)
    {
        s.push(T);
        T = T->lchild;
    }
    return T ;
}

void inOrder2(BiTNode *T) //非递归描述
{
    BiTNode *t = NULL;
    stacks;

    t = goL(T, s);

    while (t)
    {
        printf("%c ", t->data);
        //如果t有右子树 重复步骤
        if (t->rchild)
        {
            t = goL(t->rchild,s);  //右子树中中序遍历的起点
        }
        else if (!s.empty())  //如果没有右子树   根据栈顶指示
        {
            t = s.top();
            s.pop();
        }
        else //如果t 没有右子树   根据栈顶为空
        {
            t = NULL; //结束循环
        }   
    }
}


//中序遍历递归
void inOrder(BiTNode *root)
{
    if (root)
    {
        inOrder(root->lchild);
        printf("%c ", root->data);
        inOrder(root->rchild);
    }
}

int main(void)
{
    BiTree root;
    root = CreateBT();

    inOrder(root);
    cout << endl;

    inOrder2(root);
    BiTree_Free(root);

    return 0;
}

中序遍历运行结果

树的后序非递归遍历

算法思想：当 p 指向某一结点时，不能马上对它进行访问，而要先访问它的左子树，因而要将此结点的地址入栈；当其左子树访问完毕后，再次搜索到该结点时（该结点地址通过退栈得到），还不能对它进行访问，还需要先访问它的右子树，所以，再一次将该结点的地址入栈。只有当该结点的右子树访问完毕后回到该结点时，才能访问该结点。为了标明某结点是否可以访问，引入一个标志变量flag，当 flag == 0 时表示该结点暂不访问，flag ==1 时表示该结点可以访问。flag 的值随同该结点的地址一起入栈和出栈。因此，算法中设置了两个堆栈，其中 STACK1 存放结点的地址，STACK2 存放标志变量 flag，两个堆栈使用同一栈顶指针 top，且 top 的初始值为 −1。

/*
* 问题描述：树的后序非递归描述
* C/C++ 语言
*
* @author Erice_s
* [email protected]
* @date 2017/10/28
*
*/
#define MAX_STACK 50
void PostOrderTraverse(BTree T)
{
    BiTree STACK1[MAX_STACK], p = T;
    int STACK2[MAX_STACK], flag, top = -1;
    while (p != NULL || top != -1)
    {
        while (p != NULL) {
            STACK1[++top] = p;
            STACK2[top] = 0;
            p = p->lchild;
        }
        p = STACK1[top];
        flag = STACK2[top--];
        if (flag == 0) {
            STACK1[++top] = p;
            STACK2[top] = 1;
            p = p->rchild;
        }
        else {
            VISIT(p);
            p = NULL;
        }
    }
}