冷启动中的多避老虎机问题(Multi-Armed Bandit,MAB)
转载请注明出处:https://thinkgamer.blog.csdn.net/article/details/102560272
博主微博:http://weibo.com/234654758
Github:https://github.com/thinkgamer
公众号:搜索与推荐Wiki
推荐系统中有两个很重要的问题:EE问题和冷启动。在实际的场景中很好的解决这两个问题又很难,比如冷启动,我们可以基于热门、用户、第三方等信息进行半个性化的推荐,但很难去获得用户的真实兴趣分布。那么有没有一种算法可以很好的解决这个问题呢?答案就是:Bandit。
Bandit算法与推荐系统
在推荐系统领域里,有两个比较经典的问题常被人提起,一个是EE问题,另一个是用户冷启动问题。
EE问题又叫Exploit-Explore。
- Exploit表示的是对于用户已经确定的兴趣当然要迎合。
- Explore表示的如果仅对用户进行兴趣投放,很快就会看厌,所以要不断的探索用户的新兴趣
所以在进行物品推荐时,不仅要投其所好,还要进行适当的长尾物品挖掘。
用户冷启动问题,也就是面对新用户时,如何能够通过若干次实验,猜出用户的大致兴趣。
这两个问题本质上都是如何选择用户感兴趣的主题进行推荐,比较符合Bandit算法背后的MAB问题。
比如,用Bandit算法解决冷启动的大致思路如下:用分类或者Topic来表示每个用户兴趣,也就是MAB问题中的臂(Arm),我们可以通过几次试验,来刻画出新用户心目中对每个Topic的感兴趣概率。这里,如果用户对某个Topic感兴趣(提供了显式反馈或隐式反馈),就表示我们得到了收益,如果推给了它不感兴趣的Topic,推荐系统就表示很遗憾(regret)了。如此经历“选择-观察-更新-选择”的循环,理论上是越来越逼近用户真正感兴趣的Topic的。
Bandit算法来源
Bandit算法来源于历史悠久的赌博学,它要解决的问题是这样的:
一个赌徒,要去摇老虎机,走进赌场一看,一排老虎机,外表一模一样,但是每个老虎机吐钱的概率可不一样,他不知道每个老虎机吐钱的概率分布是什么,那么每次该选择哪个老虎机可以做到最大化收益呢?这就是多臂赌博机问题(Multi-armed bandit problem, K-armed bandit problem, MAB)。
怎么解决这个问题呢?最好的办法是去试一试,不是盲目地试,而是有策略地快速试一试,这些策略就是Bandit算法。
这个多臂问题,推荐系统里很多问题都与它类似:
- 假设一个用户对不同类别的内容感兴趣程度不同,那么我们的推荐系统初次见到这个用户时,怎么快速地知道他对每类内容的感兴趣程度?这就是推荐系统的冷启动。
- 假设我们有若干广告库存,怎么知道该给每个用户展示哪个广告,从而获得最大的点击收益?是每次都挑效果最好那个么?那么新广告如何才有出头之日?
- 我们的算法工程师又想出了新的模型,有没有比A/B test更快的方法知道它和旧模型相比谁更靠谱?
- 如果只是推荐已知的用户感兴趣的物品,如何才能科学地冒险给他推荐一些新鲜的物品?
Bandit算法需要量化一个核心问题:错误的选择到底有多大的遗憾?能不能遗憾少一些?常见Bandit算法有哪些呢?往下看
Thompson sampling
1、Beta分布
Thompson Sampling是基于Beta分布进行的,所以首先看下什么是Beta分布?
Beta分布可以看作是一个概率的概率分布,当你不知道一个东西的具体概率是多少时,他可以给出所有概率出现的可能性。Beta是一个非固定的公式,其表示的是一组分布(这一点和距离计算中的闵可夫斯基距离类似)。
比如:
二项分布(抛n次硬币,正面出现k次的概率)
P ( S = k ) = ( n k ) p k ( 1 − p ) n − k P(S=k)=\binom{n}{k} p^k (1-p)^{n-k} P(S=k)=(kn)pk(1−p)n−k
几何分布(抛硬币,第一次抛出正面所需的次数的概率)
P ( T = t ) = ( 1 − p ) t − 1 p P(T=t)= (1-p)^{t-1} p P(T=t)=(1−p)t−1p
帕斯卡分布(抛硬币,第k次出现正面所需次数的概率)
P ( Y k = t ) = ( t − 1 k − 1 ) p k − 1 ( 1 − p ) t − k p P(Y_k=t)=\binom{t-1}{k-1} p^{k-1} (1-p)^{t-k}p P(Yk=t)=(k−1t−1)pk−1(1−p)t−kp
去找一个统一的公式去描述这些分布,就是Beta分布:
B e t a ( x ∣ α , β ) = 1 B ( α , β ) x α − 1 ( 1 − x ) β Beta(x| \alpha,\beta) = \frac{1}{B(\alpha, \beta)} x^{\alpha-1} (1-x)^\beta Beta(x∣α,β)=B(α,β)1xα−1(1−x)β
其中 B ( α , β ) B(\alpha, \beta) B(α,β)是标准化函数,他的作用是使总概率和为1, α , β \alpha, \beta α,β为形状参数,不同的参数对应的图像形状不同,他不但可以表示常见的二项分布、几何分布等,还有一个好处就是,不需要去关系某次实验结果服从什么分布,而是利用
α , β \alpha, \beta α,β的值就可以计算出我们想要的统计量。
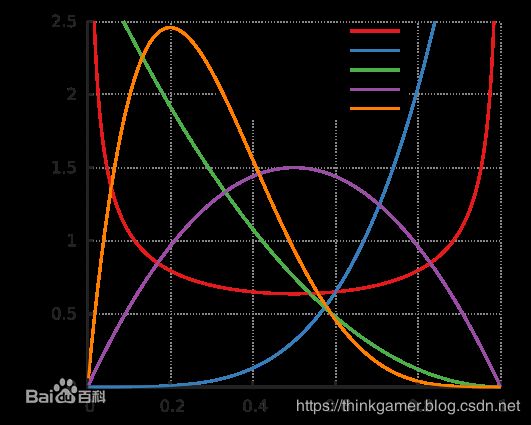
常见的参数对应的图形为:
B e t a ( α , β ) Beta(\alpha, \beta) Beta(α,β)的常见的统计量为:
- 众数为: α − 1 α + β − 1 \frac {\alpha-1}{\alpha + \beta -1} α+β−1α−1
- 期望为: μ = E ( x ) = α α + β \mu = E(x)= \frac {\alpha} {\alpha + \beta} μ=E(x)=α+βα
- 方差为: V a r ( x ) = E ( x − μ ) 2 = α β ( α + β ) 2 ( α + β + 1 ) Var(x) = E(x - \mu)^2 = \frac { \alpha \beta } { (\alpha + \beta)^2 (\alpha + \beta +1) } Var(x)=E(x−μ)2=(α+β)2(α+β+1)αβ
2、Beta分布的例子
网上资料中一个很常见的例子是棒球运动员的,这里进行借鉴。
棒球运动有一个指标是棒球击球率(batting average),就是用一个运动员击中的球数除以击球的总数,我们一般认为0.266是正常水平的击球率,而如果击球率高达0.3就被认为是非常优秀的。
现在有一个棒球运动员,我们希望能够预测他在这一赛季中的棒球击球率是多少。你可能就会直接计算棒球击球率,用击中的数除以击球数,但是如果这个棒球运动员只打了一次,而且还命中了,那么他就击球率就是100%了,这显然是不合理的,因为根据棒球的历史信息,我们知道这个击球率应该是0.215到0.36之间才对啊。
对于这个问题,我们可以用一个二项分布表示(一系列成功或失败),一个最好的方法来表示这些经验(在统计中称为先验信息)就是用beta分布,这表示在我们没有看到这个运动员打球之前,我们就有了一个大概的范围。beta分布的定义域是(0,1)这就跟概率的范围是一样的。
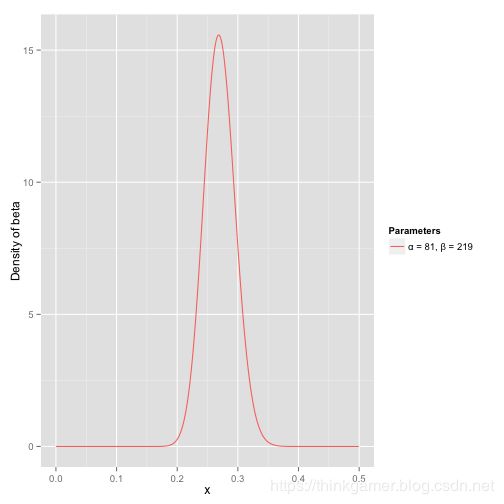
接下来我们将这些先验信息转换为beta分布的参数,我们知道一个击球率应该是平均0.27左右,而他的范围是0.21到0.35,那么根据这个信息,我们可以取 α \alpha α=81, β \beta β=219
之所以取这两个参数是因为:
- beta分布的均值是: 81 81 + 219 = 0.27 \frac{81} {81 + 219}=0.27 81+21981=0.27
- 从图中可以看到这个分布主要落在了(0.2,0.35)间,这是从经验中得出的合理的范围。
在这个例子里,我们的x轴就表示各个击球率的取值,x对应的y值就是这个击球率所对应的概率。也就是说beta分布可以看作一个概率的概率分布。
有了这样的初始值,随着运动的进行,其表达式可以表示为:
B e t a ( α 0 + h i t s , β 0 + m i s s e s ) Beta(\alpha_0 + hits , \beta_0 + misses) Beta(α0+hits,β0+misses)
其中 α 0 , β 0 \alpha_0, \beta_0 α0,β0是一开始的参数,值为81,219。当击中一次球是 hits + 1,misses不变,当未击中时,hits不变,misses+1。这样就可以在每次击球后求其最近的平均水平了。
3、Thompson Smapling
Thompson sampling算法简单实用,简单介绍一下它的原理,要点如下:
- 假设每个臂是否产生收益,其背后有一个概率分布,产生收益的概率为p。
- 我们不断地试验,去估计出一个置信度较高的“概率p的概率分布”就能近似解决这个问题了。
- 怎么能估计“概率p的概率分布”呢? 答案是假设概率p的概率分布符合beta(wins, lose)分布,它有两个参数: wins, lose。
- 每个臂都维护一个beta分布的参数。每次试验后,选中一个臂,摇一下,有收益则该臂的wins增加1,否则该臂的lose增加1。
- 每次选择臂的方式是:计算每个臂现有的beta分布的平均水平,选择所有臂产生的随机数中最大的那个臂去摇。
4、TS的Python实现
import numpy as np
import random
def ThompsonSampling(wins, trials):
pbeta = [0] * N
for i in range(0, len(trials)):
pbeta[i] = np.random.beta(wins[i] + 1, trials[i] - wins[i] + 1)
choice = np.argmax(pbeta)
trials[choice] += 1
if random.random() > 0.5:
wins[choice] += 1
T = 10000 # 实验次数
N = 10 # 类别个数
# 臂的选择总次数
trials = np.array([0] * N )
# 臂的收益
wins = np.array([0] * N )
for i in range(0, T):
ThompsonSampling(wins, trials)
print(trials)
print(wins)
print(wins/trials)
UCB
1、UCB的原理
UCB(Upper Confidence Bound,置信区间上界)可以理解为不确定性的程度,区间越宽,越不确定,反之就越确定,其表达式如下:
s c o r e ( i ) = N i T + 2 l n T N i score(i) = \frac {N_i}{T} + \sqrt{ \frac{2 ln T}{N_i}} score(i)=TNi+Ni2lnT
其中 Ni 表示第i个臂收益为 1 的次数,T表示选择的总次数
公式分为左右两部分,左侧(+左侧部分)表示的是候选臂i到目前为止的平均收益,反应的是它的效果。右侧(+右侧部分)叫做Bonus,本质上是均值的标准差,反应的是候选臂效果的不确定性,就是置信区间的上边界。
统计学中的一些统计量表达的含义
如果一个臂的收益很少,即Ni很小,那么他的不确定性就越大,在最后排序输出时就会有优势,bouns越大,候选臂的平均收益置信区间越宽,越不稳定,就需要更多的机会进行选择。反之如果平均收益很大,即+号左侧户数很大,在选择时也会有被选择的机会。
2、UCB的Python实现
import numpy as np
# 定义 T = 1000 个用户,即总共进行1000次实现
T = 1000
# 定义 N = 10 个标签,即 N 个 物品
N = 10
# 保证结果可复现,设置随机数种子
np.random.seed(888)
# 每个物品的累积点击率(理论概率)
true_rewards = np.random.uniform(low=0, high=1, size= N)
# true_rewards = np.array([0.5] * N)
# 每个物品的当前点击率
now_rewards = np.zeros(N)
# 每个物品的点击次数
chosen_count = np.zeros(N)
total_reward = 0
# 计算ucb的置信区间宽度
def calculate_delta(T, item):
if chosen_count[item] == 0:
return 1
else:
return np.sqrt( 2 * np.log( T ) / chosen_count[item])
# 计算UCB
def ucb(t, N):
# ucb得分
upper_bound_probs = [ now_rewards[item] + calculate_delta(t,item) for item in range(N) ]
item = np.argmax(upper_bound_probs)
# 模拟伯努利收益
# reward = sum(np.random.binomial(n =1, p = true_rewards[item], size=20000)==1 ) / 20000
reward = np.random.binomial(n =1, p = true_rewards[item])
return item, reward
for t in range(1,T+1):
# 为第 t个用户推荐一个物品
item, reward = ucb(t, N)
# print("item is %s, reward is %s" % (item, reward))
# 一共有多少用户接受了推荐的物品
total_reward += reward
chosen_count[item] += 1
# 更新物品的当前点击率
now_rewards[item] = ( now_rewards[item] * (t-1) + reward) / t
# print("更新后的物品点击率为:%s" % (now_rewards[item]))
# 输出当前点击率 / 累积点击率
# print("当前点击率为: %s" % now_rewards)
# print("累积点击率为: %s" % true_rewards)
diff = np.subtract( true_rewards, now_rewards)
print(diff[0])
print(total_reward)
3、UCB的推导
观测 1:假设一个物品被推荐了k次,获取了k次反馈(点击 or 不点击),可以计算出物品被点击的平均概率
当k 接近于正无穷时,p’ 会接近于真实的物品被点击的概率
p ′ = ∑ r e w a r d i k p' = \frac {\sum reward_i}{k} p′=k∑rewardi
观测 2:现实中物品被点击的次数不可能达到无穷大,因此估计出的被点击的概率 p’ 和真实的点击的概率 p 总会存在一个差值 d,即:
p ′ − d ⩽ p ⩽ p ′ + d p'-d \leqslant p \leqslant p'+d p′−d⩽p⩽p′+d
最后只需要解决差值 d 到底是怎么计算的?
首先介绍霍夫丁不等式(Chernoff-Hoeffding Bound),霍夫丁不等式假设reward_1, … , reward_n 是在[0,1]之间取值的独立同分布随机变量,用p’ 表示样本的均值,用p表示分布的均值,那么有:
P { ∣ p ′ − p ∣ ⩽ δ } ⩾ 1 − 2 e − 2 n δ 2 P\{|p'-p| \leqslant \delta \} \geqslant 1 - 2e^{-2n\delta ^2} P{∣p′−p∣⩽δ}⩾1−2e−2nδ2
当 δ \delta δ 取值为 2 I n T / n \sqrt { 2In T /n} 2InT/n (其中 T 表示有物品被推荐的次数,n表示有物品被点击的次数),可以得到:
P { ∣ p ′ − p ∣ ⩽ 2 I n T n } ⩾ 1 − 2 T 4 P\{|p'-p| \leqslant \sqrt { \frac{2In T }{n}} \} \geqslant 1 - \frac{ 2 }{ T^4} P{∣p′−p∣⩽n2InT}⩾1−T42
也就是说:
p ′ − 2 I n T n ⩽ p ⩽ p ′ + 2 I n T n p' - \sqrt { \frac{2In T }{n}} \leqslant p \leqslant p' + \sqrt { \frac{2In T }{n}} p′−n2InT⩽p⩽p′+n2InT
是以 1 - 2/T^4 的概率成立的,
当T=2时,成立的概率为0.875
当T=3时,成立的概率为0.975
当T=4时,成立的概率为0.992
可以看出 d = 2 I n T n d = \sqrt { \frac{2In T }{n}} d=n2InT 是一个不错的选择。
Epsilon-Greedy
1、算法原理
这是一个朴素的Bandit算法,有点类似模拟退火的思想:
- 选一个(0,1)之间较小的数作为epsilon;
- 每次以概率epsilon做一件事:所有臂中随机选一个;
- 每次以概率1-epsilon 选择截止到当前,平均收益最大的那个臂。
是不是简单粗暴?epsilon的值可以控制对Exploit和Explore的偏好程度。越接近0,越保守,只选择收益最大的。
2、Python实现
import random
class EpsilonGreedy():
def __init__(self, epsilon, counts, values):
self.epsilon = epsilon
self.counts = counts
self.values = values
def initialize(self, n_arms):
self.counts = [0 for col in range(n_arms)]
self.values = [0.0 for col in range(n_arms)]
def select_arm(self):
if random.random() > self.epsilon:
return self.values.index( max(self.values) )
else:
# 随机返回 self.values 中个的一个
return random.randrange(len(self.values))
def reward(self):
return 1 if random.random() > 0.5 else 0
def update(self, chosen_arm, reward):
self.counts[chosen_arm] = self.counts[chosen_arm] + 1
n = self.counts[chosen_arm]
value = self.values[chosen_arm]
new_value = ((n - 1) * value + reward ) / float(n)
self.values[chosen_arm] = round(new_value,4)
n_arms = 10
algo = EpsilonGreedy(0.1, [], [])
algo.initialize(n_arms)
for t in range(100):
chosen_arm = algo.select_arm()
reward = algo.reward()
algo.update(chosen_arm, reward)
print(algo.counts)
print(algo.values)
朴素Bandit算法
最朴素的Bandit算法就是:先随机试若干次,计算每个臂的平均收益,一直选均值最大那个臂。这个算法是人类在实际中最常采用的,不可否认,它还是比随机乱猜要好。
Python实现比较简单,这里就不做演示了。

【搜索与推荐Wiki】专注于搜索和推荐系统,尝试使用算法去更好的服务于用户,包括但不局限于机器学习,深度学习,强化学习,自然语言理解,知识图谱,还不定时分享技术,资料,思考等文章!